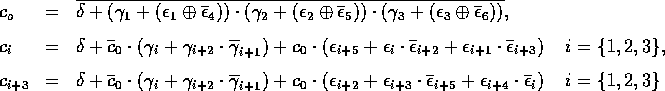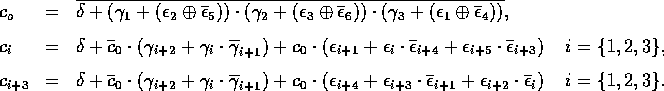I.9 : Petit résumé :
L'étude qui fait l'objet de ce mémoire a plusieurs caractéristiques et contraintes :
Domaine d'étude restreint, complexité initiale limitée et maitrisée (ou du moins le croit-on).
Utilisation d'une plateforme informatique répandue et économique.
Programmation "intelligente", élaborée et soignée, privilégiant tant que possible
la vitesse d'exécution aux dépends de la portabilité, de la vitesse de développement et
de la maintenabilité.
Travail de recherche sur l'adequation des algorithmes avec la plateforme pour
accélérer au maximum l'exécution, transformant complétement le modèle initial
pour cadrer au plus près avec la machine.
Interactivité avec l'utilisateur, disponibilité des résultats et utilisation du potentiel
du modèle utilisé.
Ces critères expliquent pourquoi ce projet ne ressemble pas à des projets classiques :
l'unique paramètre intéressant étant la vitesse, de nombreux problèmes étant précedemment
résolus de manière théoriques ou conceptuels, le défi à relever est la gestion de la
complexité croissante du projet.
Partie II : Présentation des Gaz sur Réseaux
II.1 : Introduction :
Cette partie ne peut pas et n'a pas la prétention d'être exhaustive : le sujet est trop vaste
pour pouvoir envisager d'en faire le tour complet. Il n'est pas non plus possible ici d'expliquer
(encore et encore) ce que sont les LGA : d'autres articles ou livres le font très bien.
Le lecteur novice et pressé peut consulter l'annexe B,
les explications les plus claires en français sont données en [18],
[14] et [27]. Ce mémoire discute de
la programmation d'un modèle physique, nous allons donc nous concentrer sur les notions essentielles
qui permettent de comprendre les choix de conception.
II.2 : Nomenclature :
Le terme de "gaz sur réseau", ou "lattice gas automata" en anglais (LGA) n'a pas fait l'objet
d'une étude par l'Académie Française et la première question est de savoir s'il faut mettre "réseau"
au pluriel. La réponse la plus satisfaisante consiste à considérer le réseau comme un médium, un
"ether" virtuel et digital sur lequel prennent vie des phénomènes, grâce au support physique de l'ordinateur.
Un "gaz sur réseau" désigne donc un gaz particulier (par exemple "FHP-3") alors que l'expression
"les gaz sur réseaux" désigne un ensemble de gaz aux propriétés différentes (par exemple l'ensemble des LGA
en deux dimensions).
On peut aussi trouver dans la littérature diverses dénominations pour désigner un ou des gaz sur réseaux :
"LGA", "LG" pour "Lattice Gas", "LGCA" pour "Lattice Gas Cellular Automata", GR ou GSR pour
"gaz sur réseau(x)"... Les nombreuses variantes des modèles apportent encore d'autres noms ou acronymes.
II.3 : Génèse :
L'existence des LGA est liée à plusieurs courants d'idées ou techniques. D'abord, les LGA sont une
simplification extrême des lois et des programmes de "Dynamique Moléculaire" où chaque particule
(atomes ou molécules) d'une matière est simulée avec sa vitesse, sa masse, sa direction, avec autant de
valeurs en virgule flottante pour chaque grandeur et dans chaque dimension. Ainsi, contrairement aux
méthodes d'éléments finis,
les particules sont simulées afin de laisser ressortir leur comportement individuel, au lieu de les
enfermer dans des moyennes et des interpolations. Les Gaz sur Réseaux se situent entre le monde
de la dynamique moléculaire ("MD") d'une part et les techniques volumiques classiques (Euler ou
Navier-Stokes par exemple) d'autre part, car ils apportent la capacité de simuler de plus grands
phénomènes qu'avec de la MD classique. Ils peuvent faire émerger des comportements de plus grande
échelle, accessibles seulement par les techniques d'éléments finis mais avec un niveau de détail
supérieur.
L'autre facteur déterminant pour l'existence des LGA est la démocratisation des ordinateurs. Il suffit
en fait de peu de ressources pour commencer à expérimenter sur ce type de "médium". C'est cette dépendance
technologique qui explique en partie l'historique de la méthode : tout comme pour les Automates Cellulaires
classiques, les premières expériences ont été réalisées à la fin des années 60 (Kadanoff & Swift, 1968)
et le premier modèle intensément étudié (HPP) date officiellement de 1973. Le domaine a ensuite explosé au
début des années 80 grâce à des ressources informatiques répandues et l'intérêt du public.
Les LGA ont des liens de parenté très forts avec d'autres modèles comme les Automates Cellulaires
classiques ou le modèle d'Ising, utilisés en thermodynamique ou pour étudier les séparations de phases
sans hydrodynamique. Le modèle HPP représente une convergence naturelle de toutes ces influences
et a créé un nouveau domaine hybride et fascinant.
II.4 : Un premier modèle : HPP
Les LGA sont issus de recherches de mécanique statistique, un des objectifs étant de simplifier les
lourds calculs de dynamique moléculaire pour en extraire les composantes fondamentales.
Des modèles à vélocité finie, à temps fini puis des simplifications
de plus en plus radicales (binarisation et discrétisation totale) ont donné le jour en 1973 au modèle dit "HPP"
[37]
(initiales de Jean Hardy, Olivier de Pazzy et Yves Pomeau). Ce modèle n'est pas utilisable en pratique mais
sa compréhension est importante pour des raisons historiques et techniques car il n'est pas possible
de faire plus simple (en deux dimensions). Il cristalise donc tous les défauts et toutes les caractéristiques que l'on
retrouve dans les modèles plus évolués et son étude permet de généraliser des techniques
aux autres modèles. Par exemple, les équations de collision ou la complexité algorithmique
(comme dans [31]) sont étudiées d'abord sur HPP avant d'être adaptées aux
autres modèles.
HPP ressemble à un Automate Cellulaire à voisinage de Von Neumann (carré) simple, synchrone et homogène.
Il diffère d'un Automate Cellulaire classique car chaque cellule ne possède pas d'état interne : comme noté précédemment,
le gaz sur réseau est un "médium" sur lequel transitent des particules booléennes qui s'entrechoquent
aux intersections du grillage. Les cellules sont ici appelées "noeuds" et sont le siège des collision.
Comme le tapis d'un billard sur lequel roulent les boules, les particules se déplacent sans friction
sur cet "ether" informatique.
Les frictions que l'on veut faire apparaitre sont du type hydrodynamique (par exemple la viscosité) et concernent les
interactions entre particules. Les interactions avec le médium servent à déterminer les "conditions aux limites"
(les parois ou les objets qui agissent sur le fluide). Les collisions entre les particules
déterminent le comportement du fluide et avec HPP il n'y a pas beaucoup de choix : les règles de conservation sont
strictes et il n'y a pas beaucoup de degrés de liberté. Ainsi :
- Toute collision doit conserver le nombre de particules : il y a autant de particules qui entrent
dans le noeud (afférentes) que de particules sortantes. Le contraire ne serait pas logique.
- Toute collision doit conserver l'impulsion générale des particules : en "clair", la somme vectorielle
des vecteurs mouvements de toutes les particules entrantes doit être identique à la somme vectorielle
des vecteurs mouvements de toutes les particules sortantes. Nous aurons l'occasion de revenir plus en détail
sur ce sujet bientôt.
- Il n'y a que 2^4 (16) configurations possibles pour chaque site. Les seuls quatre voisins limitent le nombre
de combinaisons intéressantes.
Pour simplifier, les collisions n'ont qu'un seul cas particulier : le "choc frontal". Toute autre configuration
est "transparente" et laisse les particules voyager librement. Le travail du programme de simulation HPP consiste
à faire voyager les particules d'un site à l'autre et de vérifier à chaque fois si un choc frontal a lieu.
Puisque toutes les quantités sont binaires, la complexité algorithmique est considérablement simplifiée
par rapport à un programme de Dynamique Moléculaire classique, où les collisions peuvent se produire
à tout moment. De plus, on économise tous les tests de collisions comme tous les types de calculs en virgule
flottante (potentiellement instables). Pourtant, même avec HPP, des phénomènes hydrodynamiques (plus ou moins
réalistes) peuvent apparaitre malgré la simplification extrême : le comportement à l'échelle macroscopique
ne dépend pas des propriétés microscopiques (par exemple, les mêmes lois permettent d'étudier les écoulements
d'air et d'eau). Les collisions des particules dans les Gaz sur Réseaux jouent un rôle crucial dans l'émergence
des phénomènes macroscopiques.
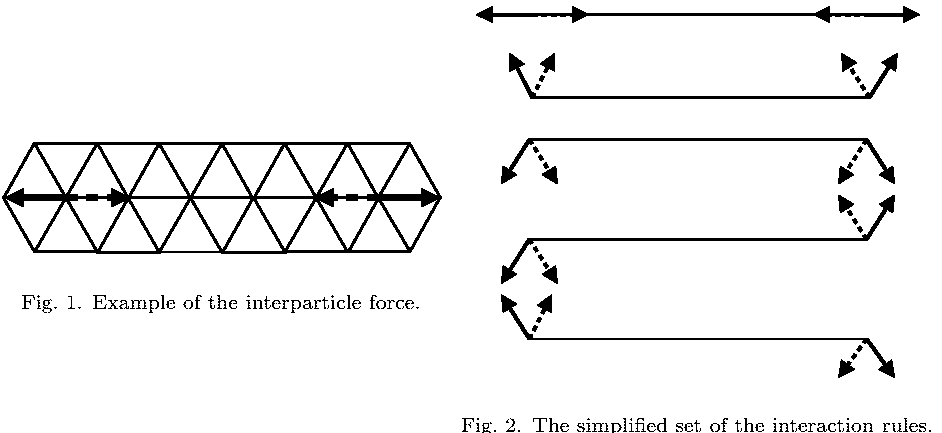
Parmi toutes les combinaisons possibles, le choc frontal est la seule qui permette de réorganiser les
particules afférentes tout en respectant les lois de conservation énoncées précédemment.
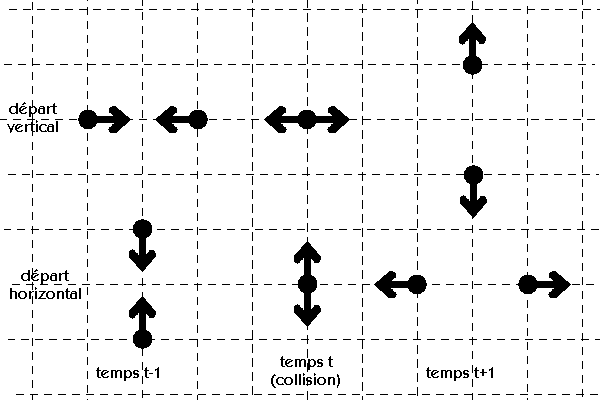
Description d'une collision frontale.
La conservation de masse et du nombre de particules est simple puisque les particules ont la même masse et
le nombre de particules afférentes est identique au nombre de particules sortantes (deux dans ce cas).
L'énergie du système est donc conservée. La conservation de l'impulsion (vecteur mouvement) est un peu plus délicate
à montrer, le dessin ci-dessous résume l'idée.
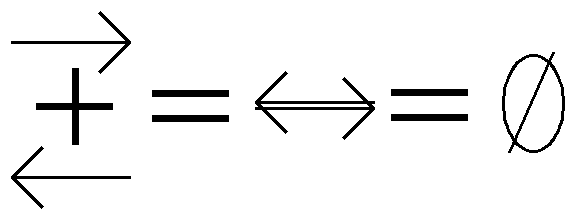
Description des vecteurs mouvements d'une collision frontale.
L'impulsion est la somme des vecteurs mouvements des particules. Le cas de la collision frontale avec HPP se résume
à additionner deux vecteurs (unitaires) de direction opposée, ce qui donne un vecteur nul. L'impulsion d'autres configuration
donnera d'autres vecteurs mais le choc frontal est la seule configuration où toutes les grandeurs énoncées
sont conservées et où l'on puisse avoir une autre configuration en sortie. Ce type d'échange de configuration
est la base de l'émergence de phénomènes d'hydrodynamique à l'échelle macroscopique et sera raffiné plus tard.
II.5 : Caractéristiques du modèle HPP :
Le choc frontal représente 12,5% du champ de collision (2 combinaisons sur 16) et se produit à une densité de 0.5
(2 particules sur 4). Par rapport aux modèles récents, le premier rapport montre une faible efficacité (faible
rapport de nombre de Reynolds par site) mais HPP est inutilisé surtout parcequ'il a quatre "invariants"
qui sont nuisibles dans la plupart des cas. Les "invariants" sont des quantités conservées dans le modèle
et qui ne correspondent pas au comportement d'un fluide réel.
- température : HPP est un modèle où toutes les particules ont la même vitesse. Or la vitesse
des particules (dans l'air par exemple) est fonction de leur température (et vice versa). Avec HPP la masse
de toutes les particules est identiques, donc leur énergie cinétique ne change pas. Il n'est pas possible
de simuler des transferts de chaleur ou tout phénomène où la température change : tout le fluide simulé
est à une température uniforme, homogène. Cela simplifie l'étude des équations caractéristiques mais interdit
d'explorer les pans les plus passionnants de la mécanique des fluides et de la thermodynamique.
- invariance de parité linéaire (désolé pour le néologisme) :
un phénomène curieux de non-répartition homogène est implicitement porté par HPP.
Il n'est pas possible de diffuser uniformément une masse de particules dans un fluide,
bien que la diffusion ne fasse pas apparaitre d'onde carrée prononcée.
Cela est dû au fait que la collision frontale, seule permise par le modèle,
ne traite qu'un nombre pair de particules par lignes.
Pour poser le problème simplement, on peut considérer que la parité du nombre de particules
sur une ligne ne change pas. L'effet indésirable n'est sensible qu'avec
des géométries très petites mais reste gênant car il est conservé dans les équations à grande échelle.
- anisotropisme : tout phénomène ne se produira pas de la même manière selon
l'orientation par rapport à la grille du gaz. Plus simplement, le fluide a un "axe de préférence", l'orientation
du médium agit indirectement sur le fluide. C'est un défaut majeur qui empêche d'étudier correctement des
tourbillons par exemple.
- invariance galiléenne : l'aspect monocinétique du fluide
empêche les tourbillons de se déplacer à la même vitesse que le fluide. Si un tourbillon apparait dans le
fluide, il sera advecté (emporté) plus vite que celui-ci (selon les cas).
En simplifiant à outrance la dynamique moléculaire, de nombreux "artefacts" liés à la discrétisation apparaissent.
Les équations qui régissent le fluide prennent toutefois un nouveau visage et l'expérimentation
informatique est plus facile. Depuis l'apparition de ce modèle, de nombreuses variantes ont vu le jour pour
atténuer ou éviter les problèmes présentés ici, ainsi que d'autres qui ont été découverts ensuite.
II.6 : Le modèle FHP :
Les Automates Cellulaires peuvent-ils résoudre des équations différentielles partielles, comme
celles de Navier-Stokes ?
Telle était la question cruciale posée par de nombreux scientifiques depuis l'apparition de ce domaine d'étude.
Rappelons que les premiers calculateurs automatiques ont été conçus dans cette optique, comme la machine à différences
finies de Babbage ou le calculateur électronique de John Vincent Atanasoff (1937-1942).
Stanislaw Ulam et Konrad Zuse dans les années 50, Stepen Wolfram et Richard Feynman dans les années 80, ont
milité pour résoudre cet épineux problème. Pourtant, ce n'est que dix ans après l'introduction du modèle HPP que
la connexion entre les deux sujets a été comprise. Uriel Frisch, Brosl Hasslacher et Yves Pomeau (d'où FHP)
ont proposé en 1986 une lègère modification qui permet de retrouver les équations différentielles de Navier-Stokes
[19].
La première modification du modèle HPP porte sur le "medium" anisotropique. Au lieu d'un maillage carré, un maillage
hexagonal est nécessaire et suffisant pour résoudre ce problème. Cette légère modification permet en fait d'augmenter
le nombre de degrés de liberté lors des collisions et d'avoir plus de possibilités de sortie différentes. Le
fluide a donc plus d'opportunités de diffuser ses particules dans chaque direction et de diminuer sa viscosité.
Les simulations deviennent soudain plus intéressantes ...
La deuxième amélioration du modèle HPP résoud "l'invariance de parité linéaire" en exploitant ces nouveaux
degrés de libertés. Le nombre de collisions équivalentes augmente et il suffit d'ajouter une nouvelle loi
de collision : la "collision triangulaire".
L'invariance galiléenne sera pour l'instant corrigée par un adimensionnement d'une grandeur. Si l'advection
d'un vortex a lieu à quatre fois la vitesse du fluide, on divisera par quatre les vitesses mesurées
pour retrouver l'invariance galiléenne (en monophasique). Cette méthode n'est plus valable avec différentes
phases mais cela sort du sujet du mémoire.
La température n'est pas un problème en soi, elle n'intervient pas dans les expériences qui intéressent les
utilisateurs de LGA. Si elle est nécessaire, la solution est simple : avoir plusieurs vitesses de particules.
Deux moyens existent : les particules elles-mêmes sautent plusieurs sites à chaque pas de temps, ou/et
les liens ont plusieurs longueurs. Les règles de collision doivent refléter ces changements tout en
respectant les règles de conservation initiales. En deux dimensions, un tel réseau est généralement le
voisinage de Moore à 8 voisins : les diagonales sont 1.41 fois plus longues que les liens horizontaux ou verticaux.
Le réseau hexagonal reste toutefois plus intéressant pour son plus grand nombre d'isométries et donc par un
plus grand nombre d'opportunités de collisions équivalentes (D2Q12 ?).
II.7 : Les règles et les nouvelles propriétés de FHP-1 :
Dans leur fameux article [19], Frisch, Hasslacher et Pomeau vont décrire une première
version du modèle FHP qui répond à la contrainte d'être nécessaire et suffisante pour retrouver les équations
de Navier-Stokes à grande échelle. Seule la partie théorique est résolue dans l'étude, l'efficacité
n'est pas au rendez-vous : les améliorations viendront plus tard, la démonstration étant déjà un grand pas.
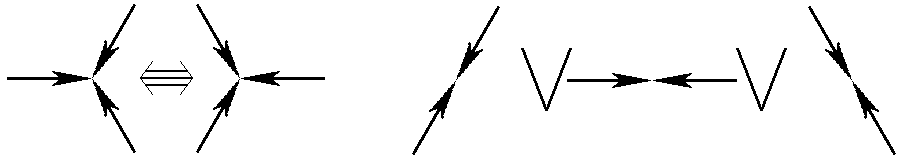
Les règles de collision du modèle FHP-1.
Le deuxième effet du changement de géométrie, après avoir brisé l'anisotropie, fut d'apporter d'autres
axes de symétrie : 3 au lieu de 2. Il y en a maintenant 64 possibilités de configuration en entrée, au lieu de 16.
Les auteurs vont introduire 2 types de collisions au lieu d'une seule, soit 5 collisions au lieu de 2 pour HPP,
si on tient compte des symétries et des rotations. On passe de 12,5 % à 12,8 % d'exploitation du champ des
collisions mais l'amélioration se situe autre part.
D'abord, la collision triangulaire améliore sensiblement la qualité de l'écoulement et permet à elle seule
de faire apparaitre des comportements hydrodynamiques réalistes. Elle permet de faire "communiquer" entre elles
des lignes et de mieux répartir les particules sur les différents axes du réseaux.
Ensuite, et c'est tout aussi remarquable : les collisions frontales n'ont plus seulement une, mais deux "voies
de sortie". Il existe trois configurations d'entrée équivalentes, équiprobables, au lieu de deux pour HPP.
Il faut donc choisir, lorsqu'un choc frontal a lieu, la configuration de sortie.
- La première solution (naïve) est de fixer
statiquement un ordre : par exemple effectuer une rotation de 60 degrés pour chaque configuration.
=> Cette solution introduit un nouvel effet parasite : la chiralité, ou préférence d'un sens de rotation,
qui est néfaste lors de l'émergence de phénomènes très turbulents. Il faut éviter de favoriser une direction
autant que possible afin de garder le fluide "pur". La chiralité peut être un moyen de simuler l'effet de
Coriolis mais ce n'est pas cohérent avec notre échelle macroscopique.
- Deuxième solution, pour les programmeurs fatigués ou pressés (comme Haarlan Stockman) : changer de chiralité
une ligne sur deux. La parité du numéro de la ligne indique si le sens de rotation est de +60 ou -60 degrés.
=> Des études [d'Humières ?] ont montré que les effets de la chiralité ne sont pas totalement effacés, principalement au niveau des
parois. Ce mauvais compromis n'est pas recommandé en pratique, même si les effets ne sont pas directement visibles.
- La solution recommandée est d'effectuer la rotation une fois sur deux, au hasard. Le générateur de nombres
aléatoires n'a pas besoin d'être de qualité indiscutable, mais suffisante pour briser la chiralité. Il doit donc
simplement être équiprobable et avoir une longue période de répétition. Dans notre programme d'expérimentation,
le nombre aléatoire est tout simplement mis à jour en fonction des sites précédents (un simple ADD avec les
sites de direction A) ce qui fournit des données de nature suffisamment indépendantes pour briser la chiralité,
après une période d'amorçage négligeable.
Si les chiralités locales sont choisies chaque fois au hasard et de manière totalement indépendante, le fluide
simulé diffère d'un fluide HPP d'une autre façon encore : il devient irréversible. Alors qu'un fluide HPP
est purement déterministe (toute configuration initiale des particules donnera une unique configuration
finale) le fluide FHP peut donner un nombre quasiment infini de configurations de sorties, selon le générateur de
nombres aléatoires. Si les nombres sont "réellement" aléatoires, le fluide correspond à un fluide réel et
il n'est pas possible de remonter à la configuration d'origine après n'importe quel nombre de pas de calcul.
Pour illustrer cette propriété incroyable, on procède parfois à l'expérience suivante : soit un programme FHP
avec une configuration des particules initiales choisies arbitrairement. Le générateur de nombres aléatoires
est déterministe et réversible.
1) Le programme est lancé et calcule T pas de temps, autant que nécessaires pour
obtenir une relaxation suffisante du fluide (une soupe brownienne bien homogène).
2) Les direction des particules sont toutes inversées et le programme est relancé avec le générateur de nombres
aléatoires tournant dans le sens inverse.
3) Après un même nombre T de pas de temps, le fluide retrouve sa configuration initiale, telle qu'au début du 1).
4) Ensuite, on restaure l'état du 2) et on change un bit, une direction de particule ou la "graine" du générateur
de nombres aléatoires. Quel que soit le nombre de pas de temps de calcul, la configuration initiale ne sera pas
retrouvée et elle restera certainement à l'état de "soupe brownienne".
Christopher Moore a démontré [31] que la prédiction du résultat d'un calcul FHP fait partie
de l'ensemble P-complet. En français, cela signifie que pour obtenir le résultat de N cycles, il faut effectuer tous
les N pas de temps les uns après les autres : il n'y a pas de court-circuit possible. Il n'y a théoriquement pas de
moyen de calculer le Nième état d'un LGA sans calculer tous les états précédents. Le calcul "brut" est la seule voie
possible pour atteindre le résultat de la simulation, les optimisations doivent donc porter sur la partie de calcul.
Le fluide FHP a des propriétés fortement non linéaires et dissipatives, ainsi que de nombreuses autres
propriétés curieuses, malgré sa simplicité étonnante. Il obéit à la loi de Mariotte et des gaz parfaits.
Il est un milieu compressible et peut donc propager une onde "sonore" de manière circulaire comme dans la nature.
Son calcul est par construction inconditionnellement stable et exact.
Mais son efficacité est mauvaise en pratique : le chemin
parcouru par une particule entre deux collisions (mean free path en anglais) est très long en moyenne,
la viscosité du fluide est forte et il faut donc des millions de sites pour simuler des phénomènes intéressants.
II.8 : Les améliorations de FHP-2 :
La première amélioration du modèle FHP original, ensuite renommé FHP-1, fut d'ajouter une "particule immobile".
Cet ajout permet de porter le nombre de configurations à 128 et de rajouter de nombreuses opportunités inespérées
pour réarranger les particules en sorties. La viscosité chute et le modèle devient plus efficace. On commence aussi
à s'intéresser aux propriétés de dualité du modèle : dans le cas du choc frontal, remplacer une particule
par un "trou" et vice versa est tout à fait valable.
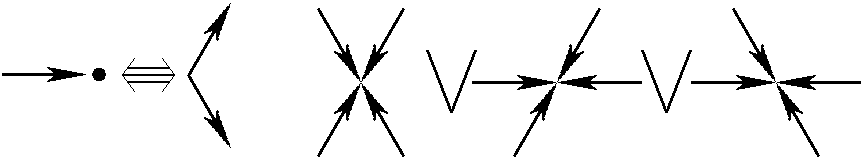
Les règles de collision additionnelles du modèle FHP-2.
La viscosité diminue et le nombre de collisions augmente : 20 entrées
mais l'occupation du champ de collision reste faible : 15 %.
Bien que les possibilités augmentent et que la définition du modèle FHP-2
ne soit pas très précise, il reste encore des efforts à faire.
II.9 : Caractéristiques particulières du modèle FHP-3 :
Le modèle sur lequel nous allons nous attarder est le modèle FHP-3. Il est une extension
du modèle FHP-2 avec une jeu de collisions saturé : 76 combinaisons sur 128 donnent
lieu à un réarrangement des particules à la sortie. 59 % : c'est le maximum d'occupation
du champ de collisions que l'on puisse obtenir avec 7 bits.
La table des collisions sera analysée en détail dans la partie IV
alors attardons-nous ici sur les raisons d'étudier ce modèle particulier.
Tout d'abord, ce modèle offre un compromis acceptable de simplicité et d'efficacité.
Il n'est pas plus avantageux de faire plus simple : les deux modèles
FHP décrits précédemment sont conceptuellement plus simples mais la surcharge en calcul
dûe aux collisions plus complexes de FHP-3 est largement compensée par la réduction du nombre de données
à traiter, donc le temps de calcul est réduit. Nous verrons aussi que les modèles FHP sont
memory bound sur la plateforme qui nous concerne, une accélération des calculs n'a
donc pas d'influence radicale sur le temps total de calcul car la mémoire est trop lente.
La programmation de FHP-3 est plus avantageuse que FHP-1 ou FHP-2 malgré une plus grande complexité.
Il n'est pas non plus envisageable à notre niveau de programmer un modèle plus efficace :
après FHP3, aucun modèle ne fait autorité et n'est suffisamment connu pour être utilisé
dans le cadre de notre étude de cas. Après FHP-3, le foisonnement d'améliorations a dispersé
les efforts et aucun nouveau modèle discret n'est assez maitrisée par le public novice. De plus,
la plus grande partie des nouveaux modèles implique une réorganisation complète des données et du programme :
nouveaux réseaux, nouvelles géométries, nouvelles lois et nouveaux artefacts à maitriser.
Enfin, notre travail doit rester une étude de cas simple et notre but n'est pas d'étudier
un nouveau modèle en profondeur : nous voulons simplement en faire fonctionner un le plus vite
possible.
FHP-3 est donc l'un des derniers modèles "stables" et connus avant la diversification
des modèles. On peut ainsi espérer que des techniques développées pour FHP-3 sont réutilisables
facilement dans les autres modèles. Ces techniques (notamment le strip mining)
et leurs implications seront ainsi facilement comprises par les utilisateurs qui les réutiliseront
et les amélioreront selon les cas.
II.10 : Propriétés physiques des modèles FHP :
Pour illustrer les propos du chapitre précédent, nous étudierons le tabelau suivant :
| modèle
| FHP-1
| FHP-2
| FHP-3
|
Cs
(vitesse du son en site par cycle)
| 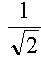
| 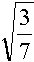
| 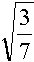
|
| g
| 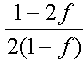
| 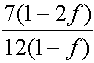
| 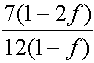
|
f*
(densité idéale, en occupation du site)
| 0,187
| 0,179
| 0,285
|
Re*
(Nombre maximal de Reynolds par site à la densité idéale)
| 0,387
| 1,08
| 2,22
|
Pour fonctionner correctement, à un nombre de Reynolds maximum, les Gaz sur Réseaux doivent être utilisés autour
d'une densité particulière qui dépend du modèle. Pour FHP-3, cette densité est heureusement simple : deux particules
par site (2/7 = 0,285). Si l'invariance galiléenne est nécessaire, la densité peut être différente.
La vitesse des écoulements doit aussi être limitée, en pratique à Mach 0.3 soit au maximum 0,6*0,3 = 0,2 sites
par pas de temps.
Puisque nous parlons ici du nombre de Reynolds, attardons-nous dans ce paragraphe sur sa définition. Pour simplifier
un peu arbitrairement, il met en relation la taille d'un objet ou d'un phénomène avec la viscosité du fluide.
Pour un gaz sur réseau, la viscosité correspond à une sorte de résistance à la diffusion d'une force ou d'une
perturbation dans toutes les directions. Ainsi, plus le nombre de Reynolds est élevé, plus les phénomènes se diffusent
et les géométries sont complexes.
Il est ainsi possible de comparer des phénomènes qui ont lieu à des vitesses différentes, à des échelles différentes,
à des pressions différentes dans des matières différentes, la complexité du phénomène est ainsi réduite à un seul
nombre sans unité. Il correspond aux équivalences suivantes, de la plus théorique à la plus pratique pour nous :
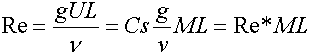 | avec | 
|
En conséquence, avec un gaz sur réseau, nous pouvons déduire le nombre de Reynolds caractéristique
d'un écoulement à partir de la vitesse (en nombre de Mach) du fluide, multipliée par la longueur caractéristique de
l'écoulement (L) et l'efficacité du modèle (Re*).
Le tableau montre que le gain en efficacité en nombre de Reynolds entre FHP-1 et FHP-3 est environ d'un facteur 6.
Il faut donc en théorie 36 fois moins de sites et 6^3=216 fois moins de temps de calcul avec FHP-3 (puisque le temps
de calcul croît environ à la puissance troisième de la longueur caractéristique). Les paramètres idéaux d'utilisation
changent aussi, tout comme les caractéristiques (par exemple la vitesse du son). Le respect de ces paramètres
est crucial pour utiliser FHP de manière optimale et sans surprise : il suffit d'un écart pour observer
des phénomènes non physiques (artifacts).
De plus, on ne reviendra jamais assez sur l'importance de l'adimensionnement
lié à l'invariance galiléenne ! A densité idéale, la vitesse du fluide doit être multiplitée par 3/10
(voir la formule du tableau avec une densité de 2/7).
Pour les Gaz sur Réseaux du type FHP, d'autres phénomènes curieux, inattendus et inquiétants apparaissent. Pour des
écoulements à pression constante, les régions à plus grande vitesse ont une plus grande densité :
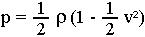 | avec |  |
| ce qui ne correspond pas à la formule normale : | 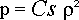 |
L'équation de Navier-Stokes pour le cas général est celle-ci :
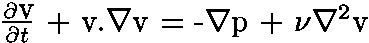
Mais pour un Gaz sur Réseau (hexagonal) à basse pression et à basse vitesse, elle devient :
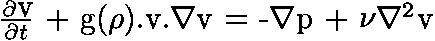
Le terme g(rho) est ajouté pour corriger l'invariance galiléenne. Il est donné dans le tableau précédent, où il dépend
de la densité. Selon les cas, il peut être intégré dans l'adimensionnement d'une grandeur (vitesse, pression, temps...).
Il faut alors choisir la densité en fonction du critère d'expérimentation, soit un grand nombre de Reynolds
ou l'invariance galiléenne, restaurée d'une manière ou d'une autre. La pression, la densité, la vitesse, la viscosité
et le temps sont ainsi enchevêtrés de manière complexe et leur étude sort du cadre de ce mémoire
puisqu'elle est disponible dans la littérature spécialisée. L'utilisateur est mis en garde du fait que la validité
des résultats dépend de la qualité de l'analyse du problème et de la compréhension intime des mécanismes mis en jeu.
Le programme seul ne pourra donner de résultat correct que dans des conditions contrôlées par l'utilisateur.
Les gaz sur réseaux FHP ne sont pas parfaits, nous le savons maintenant. Mais il y a surtout un détail
à rendre insomniaque car aucune solution simple n'est satisfaisante. Le problème peut être énoncé
de cette manière : si deux particules voyagent sur le même lien en sens inverse, elles ont moins d'une chance
sur deux pour être déviées dans un choc frontal. En conséqunce, la viscosité de FHP-3 est inférieure
à ce que le modèle pourrait fournir dans un cas idéal où tout événement d'une particule croisant une autre
donnerait lieu à une réorganisation des configurations. Le problème touche la nature même du réseau car un lien entre
deux noeuds a deux canaux unidirectionnels et indépendants. Il n'est pas possible de diviser
ce canal en deux tronçons et de tester les collisions à cet endroit car il faudrait disposer d'une autre
dimension ou direction pour réordonner les configurations à chaque temps t+1/2.
Le problème a été abandonné, les caractéristiques des réseaux existants étant estimés suffisamment satisfaisantes.
Mais surtout, il faut respecter le principe d'exclusion de Fermi qui stipule que deux particules ne peuvent pas
avoir la même position et la même vitesse au même instant.
Le dernier défaut reproché aux LGA booléens est la quantisation et le fort niveau de bruit. Il faut effectuer des
moyennes, ce qui empêche quasiment toute mesure ponctuelle. Un physicien préfère souvent 10% d'erreur à 10% de bruit
lorsqu'il veut effectuer un calcul.
Notons toutefois pour terminer que la précision d'un gaz sur réseau approche 1% dans des conditions idéales, soit
environ la précision de la mesure. Les méthodes traditionnelles sont qualitativement et quantitativement plus
imprécises en pratique et nécessitent de nombreuses mises à l'échelle ainsi que des mesures réelles.
II.11 : Extensions diverses :
Pour clore cette partie, nous allons voir quelques variations sur le thème des Gaz sur Réseaux. La première famille
conserve l'aspect binaire, ou dicret, de HPP/FHP : des modèles thermiques, comme évoqués précédemment,
ont été étudiés (géométrie D2Q9) [13]. Diverses études ont permis de mieux contrôler
l'invariance galiléenne du modèle : par exemple le modèle FHP-4 avec plusieurs particules immobiles
[20][28][29]. Des modèles à plusieurs
phases (matières) miscibles ou immiscibles permettent d'injecter des "traceurs" dans des écoulements, ou de
simuler la séparation de deux fluides (comme de l'huile se séparant de l'eau)
[9][15][16]. En 1988,
Jean-Pierre Rivet [11] programme un Gaz sur Réseau en 3D à grande échelle sur un réseau FCHC
(HyperCube à Faces Centrées). En 1990, C. Appert et S. Zaleski ajoutent des forces non locales entre
particules pour calculer la séparation de phases.
Les LGA discrets ont vite été supplantés par la famille des LGA en virgule flottante car leur rapport efficacité/temps
de calcul est plus intéressant. La disponibilité de plateformes suffisamment puissantes a permis à ce domaine
de croître au point de canaliser la plupart des efforts de recherche. Les utilisateurs de CAM-8 sont probablement
les derniers à utiliser des modèles discrets. La première raison d'utiliser les nouveaux modèles est simple :
il n'y a pas besoin d'intégrer de nombreux points pour effectuer une mesure. Les modèles discrets sont intrinsèquement
bruités et les physiciens détestent le bruit. Ce bruit est pourtant intéressant pour faire émerger des phénomènes
spontanément alors qu'ils sont forcés dans la pratique (par exemple : dissymétrie dans un tunnel pour forcer
des allées de Von Karman à apparaitre rapidement, voir la partie III.9).
Pour réduire la viscosité, les nombres en virgule flottante sont utilisés car ils ont une plage dynamique bien supérieure
à un seul bit. Toutefois on ne peut plus utiliser les techniques de collision classiques ! On utilise alors les méthodes
de Bolzman, l'opérateur BGK est le plus souvent utilisé actuellement. Le nombre de Reynolds est bien plus grand
et les mesures sont plus faciles avec un même nombre de sites, même si ces sites prennent plus de place en mémoire
qu'un site FHP. La méthode de Bolzman est utilisée dans presque tous les domaines actuellement, avec autant
ou plus de diversité que le modèle FHP, même si le débogage est encore plus difficile qu'avec FHP :
lorsque la densité n'est pas exactement conservée, on ne peut pas savoir exactement si c'est une erreur
d'arrondi, de frappe ou de formule...
Enfin, puisque le bruit est nécessaire dans certains cas, Boghossian et al. [35]
ont introduit les ILG : Integer Lattice Gases, sensés avoir à la fois les avantages des modèles discrets
et continus. Les premières expériences ont calmé l'optimisme initial, mais tout espoir n'est pas perdu.
II.12 : Conclusion :
Le modèle FHP-3 allie une simplicité relative à des caractéristiques suffisamment intéressantes pour justifier
les efforts de programmation qui sont effectués dans ce domaine. Nous avons toutefois constaté qu'il ne peut
être utilisé que dans un nombre restreint de cas et dans des conditions sévèrement contrôlées mais notre étude porte
uniquement sur les aspects architecturaux et algorithmiques de ce type de modèles. Cette deuxième partie est la seule
qui porte sur les aspects purement théoriques et nous pouvons maintenant nous intéresser aux algorithmes dans tout
le reste de ce mémoire, tout en étant conscient des possibilités et des limites du modèle.
Partie III : Présentation des travaux antérieurs
III.1 : Introduction :
Après la partie précédente, qui rappelle les points clés de mécanique qui nous concernent, cette partie
présente les techniques classiques et basiques pour programmer les Gaz sur Réseaux.
Elle est la base et le point de départ du travail réalisé pour ce mémoire.
La première implémentation de référence est donnée en annexe B : elle a fait l'objet d'un article
dans le journal Pascalissime et permet de comprendre les problèmes de base posés par le modèle FHP3.
Nous étudierons la structure et la conception du programme puis les problèmes rencontrés pour arriver à
la description d'une deuxième implémentation de référence plus sophistiquée. Enfin nous analyserons plus
en profondeur les caractéristiques de la programmation des LGA pour préparer la version de ce mémoire.
III.2 : Idées de base :
Le premier programme, écrit à l'origine en Turbo Pascal, a été inspiré par l'article de
Pierre Lallemand, paru Revue du Palais de la Découverte [18] et décrivant
approximativement le modèle FHP-2. Le seul paragraphe dans lequel la programmation est abordée est celui-ci :
"
Nous donnons d'abord quelques brèves indications sur ces expériences, pour susciter d'éventuelles vocations
auprès des lecteurs disposant d'un ordinateur personnel. Chaque noeud du réseau est représenté par un nombre
formé par la juxtaposition de sept nombres égaux à 0 ou 1 (bits) : un octet de la mémoire d'ordinateur suffira
donc pour décrire chaque site. L'évolution temporelle se fait en deux étapes :
propagation des particules par déplacement vers les noeuds voisins des bits convenables
collision en chaque noeud en allant lire dans une table préparée une fois pour toutes le résultat de la collision
particulière.
"
Mais ces indications m'ont longtemps laissé perplexe. J'ai ensuite cherché de l'aide dans les thèses de Valérie Pot
[15] et d'Umberto d'Ortona [14] à Jussieu mais aucun code
et aucune indication ne sont fournis. Pourtant, les questions suivantes sont simples :
- Que contient la table, et comment la fabrique-t-on ?
- Que représentent les bits ? Un lien ou un noeud ?
La première question est résolue par du "travail sur papier" et une analyse exhaustive des collisions possibles.
Le travail est effectué avec des représentations vectorielles des configurations afin de trouver des réorganisations
possibles. Pourtant, les efforts seuls, sans source de référence, ont donné la table des collisions de
l'annexe B
qui n'est pas complétement juste, malgré un bon début. Les progrès sont difficiles sans exemple, ce qui motive en retour
l'aspect instructif de ce mémoire. Nous reviendrons sur la constitution de la lookup table dans la partie IV.
La représentation des données est un problème tout aussi compliqué lorqu'aucune référence n'est disponible. En effet,
même s'il est clair qu'un bit peut représenter une particule et qu'un octet permet de représenter toutes les
directions, un pas de temps comporte de nombreux pas intermédiaires et le réseau représente l'état figé des particules
à un instant qui n'est pas précisé par le modèle. En effet, un pas de temps commence-t-il par une collision
ou un déplacement ? Représentons-nous les particules qui entrent ou qui sortent ? Un bit représente-t-il un lien
ou un noeud ? Comment organiser les données pour qu'elles soient facilement manipulées ?
Une fois que la transposition d'un réseau carré à un réseau hexagonal est comprise, nous pouvons partir d'un
"ether" simple et bâtir l'algorithme de calcul à partir du code de déplacement.
Tout d'abord, le calcul est effectué cycle après cycle, et l'état
du réseau représente les particules à chaque cycle, sans se préoccuper de la sous-étape (avant ou après collision
ou déplacement). Ce qui importe est le changement entre chaque cycle : une particule se propage cycle après cycle
en sautant d'un noeud à un autre. Pour effectuer ce changement, la fonction de "calcul" effectue les deux opérations
(propagation et collision), une cellule après l'autre. Effectuer les deux opérations l'une après l'autre
sur tout le réseau impliquerait la programmation de deux boucles indépendantes et augmenterait le nombre d'accès à
la mémoire. Dans tous les algorithmes qui suivront, les deux opérations sont effectuées à l'intérieur de la même boucle
pour bénéficier de la localité des registres.
La technique d'élaboration du programme est simple :
- D'abord mettre en place la boucle externe avec la préparation des pointeurs vers les données.
- Ensuite, programmer la propagation des particules : charger un octet de mémoire et distribuer
un par un tous les bits vers les noeuds voisins, avec la gestion des variables temporaires (pour éviter le
recouvrement dans certaines directions, comme expliqué dans le chapitre suivant).
- Enfin, lorsque le déplacement est fonctionnel (tous les bits se déplacent comme prévu sur le réseau),
il ne reste plus qu'à inclure la consultation de la table, juste après l'endroit où le noeud courant est lu.
Il devient clair aussi que la table, puisqu'elle est consultée entre le chargement et la distribution, doit contenir
une représentation aussi simple et complète que possible des opérations à effectuer. La table peut effectuer des
opérations complexes et réduire la taille du programme, elle concentre donc toute l'intelligence du code de collision.
L'annexe B montre deux manières de la programmer : par code explicite ou par constante à la compilation. La table
exploite ainsi le huitième bit pour effectuer la collision avec des "murs" virtuels sans ajouter une seule ligne de
code. Des effets de pesanteur ou d'attraction peuvent même être ajoutés en modifiant légèrement certaines
entrées de la table. C'en est presque trop facile ...
III.3 : Les plans temporaires :
Un aspect méconnu des programmes de ce type concerne les "plans temporaires" : le problème ne peut être appréhendé
dans toute sa complexité que lors de la programmation, lorsqu'il est déjà trop tard. Ce problème deviendra
encore plus prépondérant avec les codes de strip mining et il est important pour la suite du travail de maitriser
parfaitement l'algorithme et les données associées.
Les "plans temporaires" deviennent très important pour les géométries très larges car même avec un ordinateur
disposant de toute la mémoire vive du monde, il est important de l'utiliser correctement. Les plans temporaires
sont décris succintement dans l'annexe B et dans la partie V.6 mais étudions ici
leur théorie générale en partant d'un cas de dimension 1 (par exemple un automate cellulaire linéaire) :
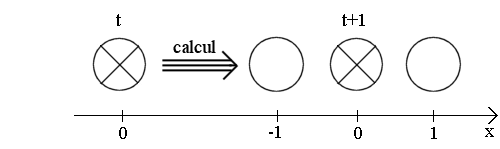
Dans un ordinateur "séquenciel", les noeuds sont traités un par un. Supposons que le sens de balayage soit
le même que le sens de x et regardons ce que ferait un algorithme simple mais mauvais :
1) d'abord il lit la valeur du noeud courant en x,
2) ensuite il calcule la valeur suivante,
par consultation de la table par exemple,
3) enfin il écrit une partie du résultat dans chaque
partie correspondante : x-1, x et x+1
4) il incrémente x et retourne en 1) si la ligne n'est pas terminée. |
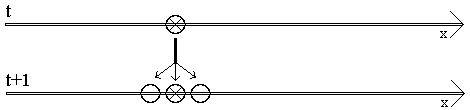
Cet algorithme est mauvais car au cycle suivant de la boucle du temps t, il trouvera en x+1
une valeur qui correspondra à t+1 et la catastrophe sera inévitable :
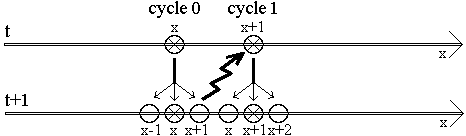
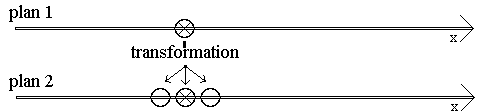
La solution la plus simple est d'utiliser deux plans de travail : un plan "source" et un plan "destination", permettant
une complexité arbitraire dans le voisinage avec l'argument choc que le "transfert" s'effectue simplement en échangeant
les deux pointeurs vers les tableaux :
Toutefois, lorsque la taille totale des tableaux atteint les limites de la mémoire de l'ordinateur, il est clair
que seule une moitié est vraiment utile car les informations sont redondantes ou inutilisées. Cette considération
devient incontournable pour les simulations en 3D car elles utilisent une quantité phénoménale de mémoire
(de 16MO à 4GO dans certains cas). L'argument de simplicité de la technique
de l'échange de pointeurs perd toute crédibilité devant ce problème.
La solution privilégiée, bien que plus complexe, utilise un "plan temporaire" pour mémoriser le résultat de chaque cycle
et éviter le "court circuit temporel" décrit plus haut. Les caractéristiques de cette mémoire dépendent de la quantité
d'informations qui doit voyager dans le même sens que celui du balayage. Pour l'exemple de l'automate cellulaire
linéaire décrit plus haut, il faut mémoriser un mot ou un bit car le déplacement se fait vers le voisin immédiat.
Au niveau de l'algorithme, cela se traduit par la nécessité de retarder l'écriture du résultat. Le programme
est doté d'une valeur temporaire (plan ponctuel) et devient ainsi :
1) lire la valeur du noeud courant en x,
2) écrire en x la valeur temporaire,
3) calculer la valeur suivante de x,
4) écrire chaque partie du résultat dans chaque partie correspondante :
x-1, x mais x+1 va dans la valeur temporaire.
5) incrémenter x et retourner en 1) si la ligne n'est pas terminée. |
Le graphe de dataflow suivant illustre une autre manière de résoudre le problème :
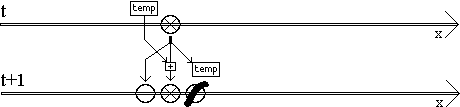
Une difficulté supplémentaire est d'amorcer le programme en fournissant une valeur initiale correspondant
à l'extrémité de la ligne : cela peut être astucieusement utilisé pour injecter des particules dans le
domaine d'étude et créer un vent artificiel. De même, la valeur finale de la variable temporaire (à la fin de la
ligne) peut être ignorée pour faire disparaitre les particules et créer une sorte de bouche de sortie
pour le fluide. Les particules peuvent ainsi être créées puis effacées à des extrémités opposées du tunnel,
ce qui génère naturellement un vent dans le tunnel. Des techniques plus sophistiquées sont cependant
recommandées car cette méthode est aussi simple que limitée dans la pratique.
Toutefois nous traitons des tableaux en deux dimensions et les choses ont tendance à s'emmêler et rendre la programmation
très délicate. Il y a pourtant une règle simple à retenir : il faut un buffer temporaire par dimension
(que la dimension soit temporelle ou spatiale) et l'information à mémoriser correspond au voyage qu'effectuent
les particules dans le sens du balayage.
Pour appliquer l'algorithme en 2 dimensions, il faut un plan temporaire indépendant pour chaque
dimension. Les colonnes sont traitées exactement de la même manière qu'une ligne
mais après projection sur la dimension perpendiculaire : ce n'est plus un noeud de mémoire
qui est nécessaire pour le plan temporaire mais toute une ligne. Pour un tableau de x * y noeuds, il faudra en tout
M = 1 + x + xy noeuds en mémoire.
En règle générale, on compte (x+1)*y noeuds pour l'allocation de la mémoire d'un tableau 2D.
La formule se généralise facilement à toute dimension N>1 et elle se réduit approximativement
à la un polynôme si toutes les dimensions sont similaires. On peut ainsi
prouver que la quantité totale de mémoire ne s'approche pas du double de la taille du tunnel comme
dans l'alternative précédente.
Par exemple, pour un réseau en 3D de dimensions (x,y,z) avec un voyage d'un noeud par pas de temps, il faudra
en tout M = 1 + x + xy + xyz noeuds de mémoire. Si x, y et z
sont des valeur rapprochées, la formule devient le polynôme suivant :
M = x^0 + x^1 + x^2 + x^3 = 1 + x + x^2 + x^3.
Elle tend ainsi vers M = (x+1)^N et permet, pour un cas donné,
d'utiliser moins de mémoire ou d'avoir un tableau plus grand, par rapport à la technique de l'échange de pointeurs
(M = 2x^N).
Naturellement, la complexité du programme augmente mais comme pour le reste cela dépend de l'expérience,
des ressources, de la patience et de la compréhension de la technique. Un cas intermédiaire (compromis
complexité/espace mémoire) serait de diviser le tunnel en de nombreuses parties et de disposer d'un plan
temporaire : chaque bloc ayant la même taille, il est facile d'utiliser la technique d'échange de pointeurs
sans pour autant doubler l'occupation de la mémoire. Cette technique ne permettant pas de réduire
directement le temps de calcul, elle n'est pas étudiée ici. De plus, les fortes contraintes en mémoire sur les PC
ainsi que les mémoires caches (principalement les modes write through et write back qui ne peuvent
pas toujours être contrôlés) favorisent la technique de plan temporaire minimal, décrite plus haut.
III.4 : Premier code de référence :
Nous allons ici étudier succintement un premier morceau de code qui servira de référence pour estimer les
performances, les contraintes et les limites des algorithmes réalisés. Il est extrait de
l'annexe B et c'est la version écrite en assembleur pour i286 en 1995 :
BEGIN
(*...*)
asm
(*...*)
(* boucle principale *)
@BOUCLE_EXTERIEURE:
mov seg_ligne,$A000
mov y,99
@BOUCLE_Y:
mov es,seg_ligne
(* PARTIE IMPAIRE: *)
(* force la particule D *)
xor cl,cl
rol rand,1
jnc @pas_retenue1
mov cl,1
@pas_retenue1:
mov bp,1 (* BP est le registre de contrôle de la boucle *)
mov di,xmax+2 (* DI pointe sur le noeud courant *)
mov si,offset temp_impair+1 (* SI pointe sur les bits E et F *)
@BOUCLE_IMPAIRE:
(* Al collectera les bits du noeud courant *)
lodsb [1]
mov byte[si-1],0 [2]
(* Ah désignera les bits à envoyer *)
mov ah,byte ptr es:[di] [3]
or ah,ah [4]
jz @vide1 [5]
(* consulte le tableau: *)
mov bl,ah [6]
xor bh,bh [7]
rol rand,1 [8]
jnc @pas_rol1 [9]
inc bh [10]
@pas_rol1:
mov ah,byte[bx+offset p] [11]
(* distribue les bits: *)
shr ah,1 [12]
jnc @pas_A1 [13]
or byte ptr es:[di-1],A [14]
@pas_A1:
shr ah,1 [15]
jnc @pas_B1 [16]
or byte ptr es:[di-xmax-1],B [17]
@pas_B1:
shr ah,1 [18]
jnc @pas_C1 [19]
or byte ptr es:[di-xmax],C [20]
@pas_C1:
shr ah,1 [21]
jnc @pas_D1 [22]
or cl,2 [23]
@pas_D1:
shr ah,1 [24]
jnc @pas_E1 [25]
or byte ptr ds:[bp+offset temp_pair],E [26]
@pas_E1:
shr ah,1 [27]
jnc @pas_F1 [28]
or byte ptr ds:[bp+offset temp_pair-1],F [29]
@pas_F1:
shl ah,6 [30]
or al,ah [31]
@vide1:
shr cl,1 [32]
jnc @pas_retenue_D1 [33]
or al,8 [34]
@pas_retenue_D1:
stosb [35]
inc bp [36]
cmp bp,xmax [37]
jbe @BOUCLE_IMPAIRE [38]
(* PARTIE PAIRE: *)
(* coupée : elle est similaire à la partie impaire *)
add seg_ligne,40
dec y
jnz @BOUCLE_Y
mov ah,1
int 016h
jz @BOUCLE_EXTERIEURE
end;
(* boucle principale *)
END. |
or byte ptr ds:[bp+offset temp_pair],E : nous atteignons ici des sommets
de programmation CISC. Rappel : le nombre réduit de registres nous oblige à
utiliser comme compteur/pointeur le pointeur de trame BP (frame Base Pointer),
alors qu'il est sensé servir pour le passage de paramètres sur la pile pour les langages
de haut niveau. Le problème est que tout adressage
utilisant BP utilise par défaut le segment de pile SS alors que les données sont adressées
par ES (le tableau dans la mémoire vidéo) et DS (les données statiques
et le plan temporaire). Nous devons donc ajouter un préfixe d'adressage ("DS:")
pour restaurer le segment, ce qui consomme inutilement des cycles.
Rappelons aussi que sur le i286, bien qu'il existe de nombreux
modes d'adressage, peu de registres peuvent être effectivement utilisés comme pointeur. Il
est donc facile de comprendre que c'est l'architecture bancale de la machine qui fait dire
à certains que "les compilateurs peuvent générer du code aussi efficace qu'un code
écrit en assembleur", puisque la flexibilité réduite diminue artificiellement les écarts
possibles de performance.
Nous voyons aussi, dans le reste du code, de nombreuses boucles, des manipulations de segments,
des calculs de pointeurs et la gestion du plan temporaire horizontal : de nombreuses
parties du programme seraient susceptibles d'être éliminées en retravaillant la structure
globale. Bien que le programme en assembleur
soit environ deux fois plus rapide que le programme en Pascal, il semble effectuer des opérations
trop complexes pour ne bouger que quelques bits. Il faut environ 38 instructions pour traiter une
seule cellule et le traitement est ralenti pour de nombreuses raisons, dont :
- l'accès aux instructions qui ne sont pas "cachées" et utilisent une partie
de la bande passante de la mémoire (le problème n'existe plus depuis le i486)
- les accès aux données en mémoire vidéo qui entrent en concurrence avec le balayage de la carte
- les nombreux sauts en avant de quelques octets qui réduisent l'efficacité de la
queue de prédécodage interne
Rappelons aussi qu'un PC à base de i286 n'a pas de mémoire cache et tous les accès à la mémoire
centrale nécessitent d'envoyer une adresse à des puces de DRAM dont le temps d'accès est environ
de 70 ns. Malgré l'apparition de chipsets sophistiqués et le début des optimisations
matérielles, les instructions du coeur de la boucle consomment de la bande passante, ce qui
entre en concurrence avec les autres accès à la mémoire. Le programme est naturellement
memory bound à cause de l'architecture du processeur.
Les mesures manuelles sur un PC i286 à 12MHz donnent une vitesse d'environ 100000 noeuds par
seconde, la géométrie étant limitée architecturalement à 320*200 par la mémoire segmentée et
la carte VGA (granularité de 64 Ko). Il y a environ une image et demie affichée par seconde
ce qui est honnorable pour un ordinateur de cette classe (comparer à l'iPSC en
D.6). La recherche des goulots d'étranglements
est difficile car le processeur i286 exécute les instructions avec des durées très variables
et le temps d'accès à la mémoire est très fluctuant. Toutefois nous pouvons effectuer quelques
estimations : le calcul d'un noeud nécessite environ 120 cycles d'horloge et 38 instructions,
soit 3,2 cycles d'horloge par instruction en moyenne.
III.5 : Influence de l'architecture :
Le passage du i286 à 12MHz au Pentium à 100MHz en 1996 fut un grand bouleversement.
Les règles de codage ont été profondément modifiées : les instructions recommandées
ne sont pas les mêmes, la mémoire cache sur deux niveaux peut enfin contenir tout le code
et toutes les données (L1 : 8Ko et L2 : 256Ko), de nombreuses innovations sont incluses...
Pourtant le mode réel ne bénéficie pas directement de toutes les améliorations, comme
par exemple les modes d'adressage étendus et orthogonaux du i386 qui permettent d'utiliser
toutes les combinaisons de registres pour accéder à la mémoire.
La mémoire virtuelle en mode protégé reste un problème car la manipulation des
registres de segments déclenche de longues séquences de microcode pour vérifier la validité des
adresses, ce qui en plus peut déclencher des exceptions pour gérer les pages en mémoire et
sur le disque dur s'il faut les swapper. On s'attend donc naturellement à ce que le programme
fonctionne moins vite lorsqu'il est lancé à partir de Windows. Pourtant, il s'y exécute visiblement
plus vite ! Plus précisément, en mode fenêtré, il s'exécute beaucoup plus vite qu'en mode
normal/"plein écran".
Le changement d'architecture, du 286 au Pentium, a changé complétement les rapports entre les
flux de données et d'instructions. L'introduction de deux niveaux de mémoire cache balance
la plus grande latence relative de la mémoire vidéo. De plus, l'accès à la mémoire vidéo subit de
nombreuses restrictions : par exemple, elle est accédée au travers du bus PCI et elle n'est pas
cachable. L'expérience avec Windows a montré la situation paradoxale où un programme "optimal" pour le
286 est inefficace sur Pentium. Pour expliquer cela, il faut préciser que Windows (en mode fenêtré)
émule la mémoire vidéo : il redirige les accès vidéo vers la DRAM centrale grâce
à la translation d'adresse du mode protégé/paginé. Ainsi, nous n'accédons pas nous-mêmes
à la mémoire vidéo, c'est l'émulateur qui copie la DRAM périodiquement vers la vraie carte.
La mémoire centrale étant cachable, les accès sont beaucoup plus rapides et le
transfert par bloc vers l'écran est plus rapide qu'octet par octet. Les instructions de type
read-modify-write sont encore plus lourdes puisqu'elles nécessitent
une lecture (blocante, pour éviter toute modification intempestive au milieu de l'instruction)
puis une écriture et il faut une transaction complète sur
le bus PCI (attente que le bus soit libre - envoyer l'adresse - envoyer/recevoir la donnée)
pour transférer un simple octet ou un bloc entier.
Le calcul en mémoire cachable puis le transfert par bloc (ou en rafale, burst pour le PCI)
est forcément plus rapide que le premier programme.
Le diagramme ci-contre est extrait de [33]. Il représente une
carte mère aux caractéristiques suivantes :
* Processeur Pentium 100MHz avec 2 caches intégrées de 8Ko chacune
* Bus local : données 64 bits, 66 MHz, 528Mo/s théoriques
* Cache L2 de 256Ko avec des puces SRAM à 15 ns de temps d'accès (sans compter
les latences de gestion de la LRU et de la SRAM de "tag" à 15 ns aussi)
* Mémoire DRAM à 70ns de temps d'accès (30ns en mode page), EDO possible.
* Bus PCI multiplexé à 33MHz et 32 bits de large (132Mo/s théoriques)
| 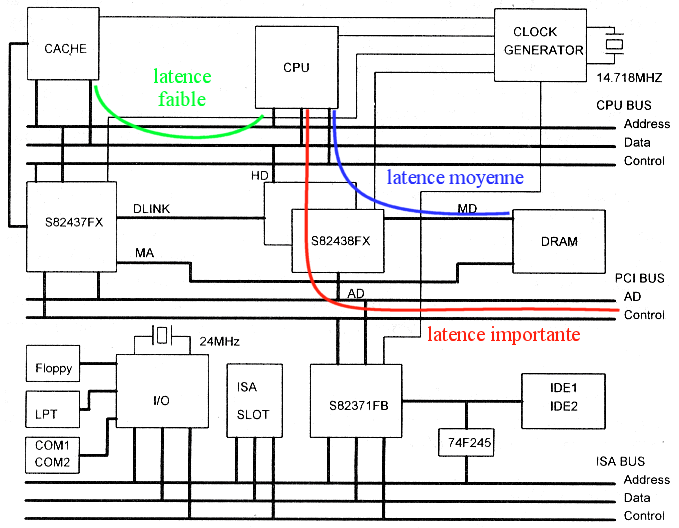 |
Nous pouvons y voir que le nombre de circuits et de connexions à traverser
est proportionnel à la latence et à la vitesse de transfert. Le circuit imprimé
montre en plus que cela est proportionnel à la distance parcourue dans les fils :
la mémoire cache est très proche du processeur alors que les slots PCI et DRAM
sont éloignés.
Des mesures réelles sur cette plateforme, en conditions "idéales", donnent une
vitesse de transfert unidirectionnel de 28Mo/s vers la carte vidéo. En pratique,
le processeur peut donc afficher un mot de 32 bits tous les 4 cycles, soit une
instruction d'affichage entrelacée avec sept instructions de calcul. Il n'est pas
raisonnable dans ces conditions d'utiliser le premier code de référence qui utilise
de nombreuses opérations complexes vers la mémoire vidéo.
La leçon est simple : en mode "normal" (MS-DOS) il ne faut plus utiliser la mémoire vidéo pour
stocker le tunnel. Il faut au contraire utiliser une méthode qui paradoxalement prendrait plus
de temps si l'on ne regardait que le nombre d'instructions à exécuter. Le calcul doit donc
s'effectuer dans la mémoire centrale et, comme l'émulateur MSDOS de Windows le faisait,
afficher régulièrement le résultat à l'écran, tous les N pas de temps (N pouvant varier
à la demande de l'utilisateur). Nous évitons ainsi de perdre du temps dans les transactions
"blocantes" du bus PCI, dont le temps d'accès est probablement supérieur à 100ns (carte vidéo
comprise). Pour qu'un programme tourne vite, il est crucial de placer les données au meilleur
endroit.
III.6 : Deuxième code de référence :
Le second code de référence date de 1997 et est inclus ci-dessous. L'idée directrice est de réduire
le code de distribution des bits en groupant les noeuds par quatre. Le réseau est alors
tourné à 90 degrés et il n'y a plus de code pour les lignes paires et impaires, comme pour le circuit
décrit en V.6. Ce code est destiné aux plateformes à partir du i386 et "optimisé"
pour le Pentium classique (P53C) où nous pouvons utiliser les registres sur 32 bits au lieu de 16.
La boucle externe affiche les calculs puis traite N pas de temps de cette manière :
;
; BALAYAGE:
;
mov ebx,es:[640]
mov XB,ebx
mov di,640
boucle_ext:
mov bx,320
boucle_int:
mov word ptr X,bx ;U (1)
;
; déplacement des variables:
;
mov esi,XC ;*V [3]
mov ebx,es:[di-316] ;*prefixe + U (3) [6]
mov XD,esi ;*V [8]
mov XC,ebx ;*U (4) [10]
mov edx,X1 ;*V [12]
mov eax,XB ;*U (5) [14]
mov ecx,es:[di+4] ;*préfixe+U (7) [17]
and edx,010000000h ;XE ;*V [19]
mov X1,eax ;*U (8) [21]
mov XB,ecx ;*V [23]
mov ebp,XA ;*U (9) [25]
mov ebx,es:[di+320] ;*préfixe+U (11) [28]
and ebp,020000000h ;XF ;*V [30]
mov XA,ebx ;*U (12) [32]
or ebp,edx ;*V [34]
;verticaux:
and eax,0C0C0C0C0h ;*U (13) [36]
and esi,008080808h ;*V [38]
and ebx,001010101h ;*U (14) [40]
or eax,esi ;*V [42]
;XL
mov ecx,XD ;*U (15) [44]
or eax,ebx ;report des verticaux *V [46]
mov ebx,XA ;*U (16) [48]
and ecx,000100010h ;*V [50]
and ebx,000002000h ;*U (17) [52]
or ebp,ecx ;*V [54]
mov ecx,X1 ;*U (18) [56]
or ebp,ebx ;*V [58]
and ecx,000201020h ;*U (19) [60]
or ebp,ecx ;*U (20) (dépendance sur ECX) [62]
;XR:
mov ebx,XB ;*V [64]
rol ebp,8 ; report XL *U (21) [66]
mov ecx,XC ;*V [68]
or eax,ebp ; report XL *U (22) [70]
mov ebp,XD ;*V [72]
and bx,2 ;U (23) [72']
and ebp,000040000h ;*V [74]
and cx,4 ;U (24) [74']
mov edx,XA ;*V [76]
or bx,cx ;U (25) [76']
mov ecx,X1 ;*V [78]
or bp,bx ;U (26) [78']
and edx,002000200h ;*V [80]
or ebp,edx ;*U (27) [82]
and ecx,004020400h ;*V [84]
or ebp,ecx ;*U (28) [86]
ror ebp,8 ;*V [88]
or eax,ebp ;*U (29) [90]
; détermine quelle banque LUT on utilise:
rol word ptr seed1,1 ;U (32) 3 cycles + non pairable [94]
setc bh ;U (35) microcode [97]
mov bl,ah ;U (36) dépendance sur EBX [98]
mov ah,[offset p+bx]
; accède au tableau (#1) U (38) AGI sur EBX, préfixe possible [101]
mov bl,al ;U (39) dépendance sur EAX [102]
mov al,[offset p+bx]
; accède au tableau (#2) U (41) AGI sur EBX, préfixe possible [105]
ror eax,16 ;U (42) dépendance sur EAX [106]
mov bl,ah ;U (43) dépendance sur EAX [107]
mov ah,[offset p+bx]
; accède au tableau (#3) U (45) AGI sur EBX, préfixe possible [110]
mov bl,al ;U (46) dépendance sur EAX [111]
mov al,[offset p+bx]
; accède au tableau (#4) U (48) AGI sur EBX, préfixe possible [114]
ror eax,16 ;U (49) dépendance sur EAX [115]
;writeback:
mov bx,word ptr X ;V [115']
mov ecx,[offset temp+bx] ;**U (50) [117]
mov [offset temp+bx],eax ;*V [119]
mov es:[di-320],ecx ;préfixe+*U (51) [122]
add di,4 ;V [123]
sub bx,4 ;U (52) [123']
jnz boucle_int ;V [124]
cmp di,63360
jbe boucle_ext |
La boucle interne comporte 67 instructions pour traiter 4 noeuds, soit environ 17 instructions par noeud :
c'est deux fois mieux que le code de référence en mode 8 bits.
Une estimation "statique", rapide et optimiste de ce kernel sur un Pentium classique fait penser qu'il peut
s'exécuter en 52 cycles (voir les nombres entre parenthèses, soit 13 cycles par noeud).
Mais en réalité, le code a été conçu pour être
exécuté en mode réel (16 bits sous MS-DOS) et l'utilisation des registres en mode 32 bits ajoute un préfixe de taille, invisible dans la syntaxe, à
chaque instruction : cela brise complétement le pairage des instructions !
La plupart des dépendances de données entre les registres ont été aplanies dans le code de mouvement afin
d'exécuter deux instructions par cycle sur le Pentium mais les préfixes de taille étaient oubliés dans l'analyse.
Les instructions marquées d'un astérisque prennent ainsi deux cycles au lieu d'un demi-cycle !
Cela montre bien que le nombre d'instruction, le temps d'exécution et le nombre de sites traités par seconde
sont des valeurs qui ne sont plus naturellement ou simplement proportionnelles : l'architecture complexe du Pentium
a des "cycles cachés" qui n'apparaissent pas en lisant le code source, même en assembleur ! Alors que ce code
est très bon pour le i386, le Pentium a un pipeline différent qui favorise certains types de codes
tout en pouvant exécuter les autres programmes mais à une vitesse nettement inférieure et sans prévenir.
L'analyse sous ce nouvel angle (voir les nombres entre crochets)
donne environ 124 cycles (comme pour la version i286, mais 31 cycles par noeud). Cette baisse incroyable
des performances, malgré le soin apporté au code, a motivé la conception d'un DOS-extender pour la suite du projet.
Le code de mouvement a été assez bien réduit mais reste lourd et consomme tous les registres.
L'analyse du code révèle aussi que le processeur effectue des opérations inutiles ou perd du temps à manipuler
des données entre les registres. Ainsi, la consultation des tables, en raison du faible nombre de registres disponibles,
du jeu d'instructions, des préfixes et des dépendances croisées, prend 20 cycles au moins, bien qu'en théorie cela
nécessite 4 cycles pour un cas "simple et idéal".
|
La densité globale dans le domaine d'étude peut être déterminée en accumulant le nombre de particules
à chaque pixel. Nous voyons ici une accumulation sur 8 bits avec deux dépassements (les mêmes couleurs sont utilisées
deux fois pour des densités différentes) et un écoulement de Poiseuille caractéristique. L'image peut être calculée
interactivement (les paramètres peuvent être changés) en une minute environ.
|  |
L'accumulation doit commencer après la stabilisation du fluide et la disparition des ondes de choc.
Il faut ici pouvoir gérer trois tableaux de 64 Ko, ce qui est à la limite des possibilités du
mode réel du x86. Avec un code de ce type, il a fallu deux heures à un Pentium à 100 MHz
pour calculer l'image suivante :
 |
A chaque pas de temps, la densité de chaque noeud est accumulée sur 16 bits dont nous voyons ici les 8 bits de poids
fort. Il faut donc un tableau de 128Ko en mémoire et accéder en tout à plus de 200Ko, ce qui a nécessité
l'emploi du mode flat (ou unreal). Ce programme est donc difficilement transportable et nécessite
une configuration très précise pour fonctionner.
|
Le bruit au niveau de l'octet de poids fort est réduit mais il a fallu beaucoup de temps de calcul
pour que toute la dynamique de l'octet soit utilisée et donne une image utilisant toutes les couleurs
de la palette (plus de 64K*3=200000 pas de temps). La vitesse de rafraichissement pour ce type de
code sur cette machine atteint environ 10Hz et la taille est fixée à 320x200 noeuds, c'est à dire
la résolution de l'écran.
III.7 : Conditions aux limites et effets de bords :
Les LGA permettent de calculer les équations différentielles de Navier-Stokes dans
des conditions idéales de très faible vitesse et de taille infinie du réseau [19].
Toute autre condition ne permet d'effectuer qu'une approximation, par exemple lorsque la taille est finie
(limitée par la taille de la mémoire de l'ordinateur), ou alors
la simulation ne correspond pas aux réalités physiques. Entre autres exemples, la vitesse du fluide
ne doit pas dépasser Mach 0,3 environ mais en plus des limites théoriques, les limites pratiques
sont aussi difficiles à connaitre et à comprendre.
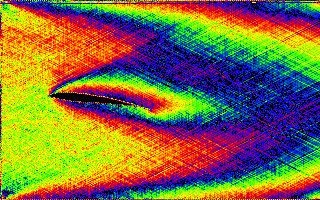
Nous allons étudier en particulier le cas d'une éprouvette dans une soufflerie ainsi que
les effets de bords liés aux conditions aux limites.
Dans les images précédentes, nous pouvons observer certains phénomènes qui influencent la simulation
et ses résultats. Tout d'abord, avant chaque pas de temps, le vent est généré par une boucle
qui crée de nouvelles particules afin de générer un "vent" dans le tunnel. Les propriétés de ce flux ont
des conséquences directes sur le temps de disparition des phénomènes transitoires et indésirés.
La manière la plus simple, comme le permet l'algorithme de plan temporaire décrit précédemment,
est de créer une particule directement dans le sens du vent. Cela correspond bien à
la théorie mais dans la réalité, un vent n'est pas constitué de particules allant toutes
dans la même directions : ce serait un vent supersonique ! De plus, les phénomènes dépassant
Mach 0,4 ne sont pas fidèles à la réalité. Il faut donc créer un flux d'air,
non une masse homogène ou homocinétique irréelle. La vitesse et la direction des particules doivent être
bien choisies. La vitesse des particules ne peut pas être modifiée car elle est unitaire :
la vitesse du flux sera réglée par la "vitesse" d'introduction et de destruction des particules
de chaque côté du tunnel. Une autre méthode est de "forcer" certaines particules au hasard
dans le tunnel en changeant leur direction mais c'est plus compliqué car le tunnel devra être
bouclé sur lui-même comme un tore, ce qui implique qu'en se propageant, les turbulences se
retrouveront en amont et se perturberont elles-mêmes. Cette méthode est adaptée à d'autres
cas (étude d'un cisaillement pour déterminer la viscosité par exemple) mais pas à celui des
simulations qui nous intéressent (même si ce n'est pas le domaine le plus adapté pour les LGA).
Pour créer un vent, nous introduisons des particules à un certain ryhtme, qui est contrôlé
au clavier par l'utilisateur dans les expériences réalisées. Leur direction est aussi importante :
elle doit être décorrélée, aussi aléatoire que possible, pour éviter que les caractéristiques
du vent n'influencent ou ne perturbent les phénomènes en aval. Pour décorréler un signal, il suffit
de le moduler par un signal connu pour être aléatoire : nous disposons déjà de phénomènes explicitement
aléatoires au niveau de certaines configurations de collision. La technique est alors de créer des
particules allant en sens inverse du vent pour, si elles en ont le temps, frapper le mur adjacent.
Cela crée une zone de haute densité propice à de nombreuses collisions, favorisant
une répartition aléatoire et naturelle des particules,
même si elles sont créées de manière déterministe. Leur surnombre local et la configuration de la paroi
forcent ainsi un flux de particules aléatoires dans le sens désiré (en moyenne). L'entropie du modèle
leur assure une répartition naturellement équilibrée dans le temps et dans l'espace.
Le deuxième problème important concerne les autres conditions aux limites. D'abord, les parois
horizontales (supérieure et inférieure) sont "rugueuses" : le modèle le plus simple spécifie que les particules
repartent par le lien où elles étaient venues. Ensuite, la paroi de droite est totalement
"absorbante" et fait disparaitre toutes les particules. Dans la réalité,
cela correspondrait à un tuyau débouchant dans le vide sidéral, ce qui n'est pas notre intention :
une veine de soufflerie réelle maintient une densité assez homogène autour du domaine d'étude et le vent
n'est pas "avalé" d'une manière ou d'une autre. Les conditions sont réunies pour faire apparaitre
un écoulement parabolique de Poiseuille qui interfère avec le domaine d'étude comme dans l'image
de densité sur 8 bits. La densité n'est pas homogène ni linéaire autour de l'éprouvette et le phénomène
de portance que l'on veut mettre en évidence est perturbé par l'influence des parois et de la disparition
des particules, ce qui est similaire à une anisotropie de la pression dans tout le tunnel.
La solution adoptée pour l'expérience suivante (l'accumulation sur 16 bits)
est de rétablir la pression dans le tunnel
grâce à une sorte de "peigne" qui piège une partie des particules qui allaient disparaître.
De proche en proche, elles créent une pression qui s'oppose en partie à leur disparition totale :
le fluide devient plus homogène et les directions des particules sont plus diverses. Nous voyons
sur l'image de densité 16 bits que le profil n'est plus parabolique, bien que les parois rugueuses
laissent subsister de légères perturbations locales.
La pression dans le tunnel est mieux répartie et équilibrée.
Une deuxième solution pour réduire encore plus, ou anihiler, l'écoulement parabolique est de rendre les
parois glissantes pour que leur vitesse par rapport au vent ne soit pas changée.
Cette solution a par exemple été adoptée pour l'allée de von Karman dans l'exemple de
David Hanon en III.9.
Cela n'a pas été essayé dans les premiers codes car le programme ne le permettait pas encore, seules les
parois rugueuses pouvant être codées dans un octet.
En complément de la première solution, nous disposons alors d'un domaine d'étude dont la pression
et la vitesse sont homogènes et favorables pour étudier des phénomènes turbulents comme les
allées de von Karman. Dans le cas contraire, par exemple si l'écoulement
de Poiseuille subsistait, il faudrait agrandir le tunnel de manière à ce que les paraboles
n'interviennent pas substanciellement dans les mesures, ce qui augmenterait quadratiquement
les besoins de mémoire et de temps de calcul.
Pour que ces conditions aux limites soient remplies, il faut plus de flexibilité dans le programme.
La nature du modèle FHP permet d'ajouter facilement les fonctions désirées mais leur implémentation
est souvent une aventure plus complexe que l'on pourrait s'y attendre. De plus, le bon sens des
équations classiques contredit la réalité microscopique des particules : les equations d'Euler ne
traitent pas explicitement du mouvement chaotique brownien. Un bon programme de calcul FHP a donc besoin de parois
glissantes comme rugueuses et d'un contrôle sûr de la création et de la destruction des particules.
Les algorithmes vus jusqu'à présent ne permettent pas de tel contrôle sur la rugosité des parois.
III.8 : Remplissage et redimensionnement dynamique du tunnel :
Une fois le fluide en régime "stationnaire", c'est à dire lorsque tous les phénomènes transitoires
(comme les ondes de choc ou les phénomènes anisotropiques hexagonaux) ont disparu, on effectue les
mesures et on réfléchit aux calculs suivants. En d'autres termes, une grande partie des calculs a
pour seule fonction d'éliminer les transitoires. Une formule empirique : t=4*(h+l)
donne le nombre de pas de temps à calculer pour que disparaisse la plupart des ondes de choc, soit deux
à trois allers et retours de l'onde de paroi à paroi. Or les simulations les plus intéressantes sont les plus
grosses et le temps de calcul augmente très vite ; en utilisant la formule précédente, il faut environ :
N=4*(h+l)*h*l pas de calcul en tout, ou environ N=8*l^3 si h
et l sont proches. Dans ce chapitre, nous allons explorer des moyens de réduire ce temps
de calcul.
Pour commencer, nous pouvons constater que la veine de simulation FHP est souvent vide au début
de l'expérience. Il faut l pas de temps et h*l*l = hl² calculs de site
pour remplir le tunnel en particules. Ce sont autant de cycles facilement gagnés si la veine contenait déjà
des particules !
Le problème est maintenant : comment remplir le tunnel ? Il est facile de le remplir uniformément
de particules, ou avec des particules au hasard, mais d'une part c'est trop simple et d'autre part
il faut gérer le cas délicat des éprouvettes qui seraient remplies de particules. En effet, la forme
que l'on place dans le tunnel n'est pas obligatoirement "pleine" et il faut que l'algorithme de remplissage
tienne bien compte de ce cas de figure. Comme dit plus haut, un algorithme simple ne convient pas et
il faut utiliser un algorithme de remplissage "intelligent" tel qu'on le rencontre dans les logiciels de
dessin bitmap (exploration récursive ou floodfill).
La première simplification oubliait aussi que ce qui nous intéresse est d'obtenir un état le plus proche
possible du régime stationnaire. Or le cas le plus simple consomme beaucoup de temps dans la mise
en mouvement le fluide. Une possibilité serait d'utiliser une résolution statique et approximative
des équations d'Euler ou de Navier-Stokes pour "guider" le remplissage préliminaire du tunnel. La limitation
ne se situe pas dans la charge de calcul mais dans sa complexité qui augmente avec celle de la géométrie des
parois. De plus, ce n'est pas un sujet qui nous concerne dans cette étude.
Une autre méthode serait d'utiliser les modèles plus simples comme FHP-2 ou FHP-1 pour effectuer une
première passe dans le fluide. Ces modèles sont plus a priori rapides à calculer et peuvent effectuer
une première approximation,
ce qui est intéressant puisque nous abandonnons la technique de consultation de table. Nous verrons pourtant que
le calcul a une importance aussi grande que le déplacement des données ("FHPIII est memory bound") et cette
méthode ne réduit pas le nombre de mouvements de particules. Toutefois, nous avons vu dans la partie précédente
que la principale différence entre les versions du modèle FHP concernent la viscosité, ou le nombre de Reynolds
par noeud. Si nous pouvons calculer à un nombre de Reynolds plus faible, nous avons donc intérêt à réduire
le nombre de noeuds plutôt que d'augmenter la viscosité : le programme de calcul reste identique mais nous
pouvons réduire le nombre de déplacements en réduisant la taille du tunnel lors de l'amorçage du fluide.
Pour réduire le temps total de calcul, nous avons donc intérêt à commencer avec une version dont la taille
est une fraction de la taille réelle. En pratique, le programme de ce mémoire limite la largeur minimale à
256 noeuds. Nous pouvons donc amorcer le tunnel avec cette largeur, durant le temps nécessaire à la disparition
des transitoires, soit environ 2000 pas de temps. Ensuite, le tunnel est agrandi : le cas le plus simple
est un doublement de toutes les dimensions et un quadruplement aisé du nombre de cellules et de leur contenu
(le contenu est recopié dans 3 cellules voisines). Le calcul continue et fait disparaitre les transitoires
liées à l'agrandissement soudain du tunnel. La procédure de calcul/agrandissement est réitérée jusqu'à obtenir
la taille désirée pour l'expérience. Il est alors possible d'accélérer considérablement le temps de calcul
nécessaire à l'établissement du régime stationnaire.
Etudions l'exemple d'une simulation dans un tunnel de dimension l=3h avec l'intention d'effectuer
une ou des mesures brèves lorsque le régime transitoire a disparu. Dans notre cas, la largeur minimum est
de 256 noeuds, la hauteur est donc de 256/3=86 noeuds. Le temps de stabilisation du fluide est environ de
4*(256+86)=1400 pas de temps soit 1400*256*86=30 millions de calculs de sites. Ensuite, le tunnel peut être
agrandi et contenir 512*172 noeuds. Le calcul redémarre alors pendant un temps nécessaire pour que le fluide
s'adapte au nouveau nombre de Reynolds, mais toutefois moins que le temps nécessaire pour l'amorçage du fluide :
environ 2*(512+172)=1400 pas de temps et 1400*512*172=123 millions de sites. Nous pouvons continuer
ainsi à calculer et agrandir jusqu'à ce que la mémoire soit saturée ou le nombre de Reynolds désiré soit
atteint. Dans notre cas, avec une limitation à 64MO, nous obtenons le temps de calcul total suivant :
taille pas de calcul sites calculés
256*86=22016 4*(256+86)=1400 30M
512*172=88064 2*(512+172)=1400 123M
1024*344=352256 2*(1024+344)=2800 986M
2048*688=1409024 2*(2048+688)=5600 7890M
4096*1376=5636096 2*(4096+1376)=11200 63124M
8192*2752=22544384 2*(8192+2752)=22400 504994M
total : 577 Milliards de sites calculés
L'agrandissement progressif permet de diviser par deux le temps d'amorçage
du fluide : en commençant à la taille prévue au départ (8192*2752) il faudrait
calculer 10^12 sites au moins ! A la fin du calcul, les 22400 pas de temps sont largement
suffisant pour effectuer les mesures désirées, grâce à des moyennes dans le temps et dans l'espace.
Il faut maintenant mentionner au moins trois limitations pratiques importantes, liées à la
complexité des phénomènes. Nous atteignons un nombre de Reynolds idéal d'environ 5000
et le type de programme présenté jusqu'à présent ne convient plus. La première limite concerne le temps de calcul :
si l'ordinateur calcule un million de sites par secondes (comme dans le deuxième code de référence)
il faudra une semaine pour calculer les 577 Milliards de sites de l'expérience. Nous sommes
encore loin du "temps réel" et de l'interactivité désirés. Ensuite, les programmes actuels utilisent
le PC sous MS-DOS en mode réel, ce qui limite les expériences à 320*200 points, il n'est pas possible
d'atteindre ainsi des nombres de Reynolds intéressants et justifiant les efforts de programmation.
Enfin, bien que le redimensionnement soit une étape relativement simple à programmer, il devient plus compliqué
de définir les parois par de simples bitmaps ou par programmation au cas par cas. Il faut donc utiliser
un mode de représentation vectoriel qui sera réinterprété à chaque fois que le tunnel change de taille.
Les vecteurs sont simples à gérer mais leur représentation intermédiaire dans le code du projet actuel
est très complexe.
III.9 : Etude d'un cas réel : benchmark de von Karman :
Afin de pouvoir comparer les résultats et l'efficacité de la méthode employée, nous utiliserons
les données fournies par une étude allemande [36], décrivant les conditions
de simulation d'allées de von Karman. Puisque nos LGA simulent les fluides de manière explicitement
temporelle en 2D, nous ne nous intéresserons qu'à la partie correspondante du benchmark qui comporte
des expériences en 2D et en 3D, en statique ou en dynamique.
Géométrie du tunnel et conditions aux limites : (extrait de [36])
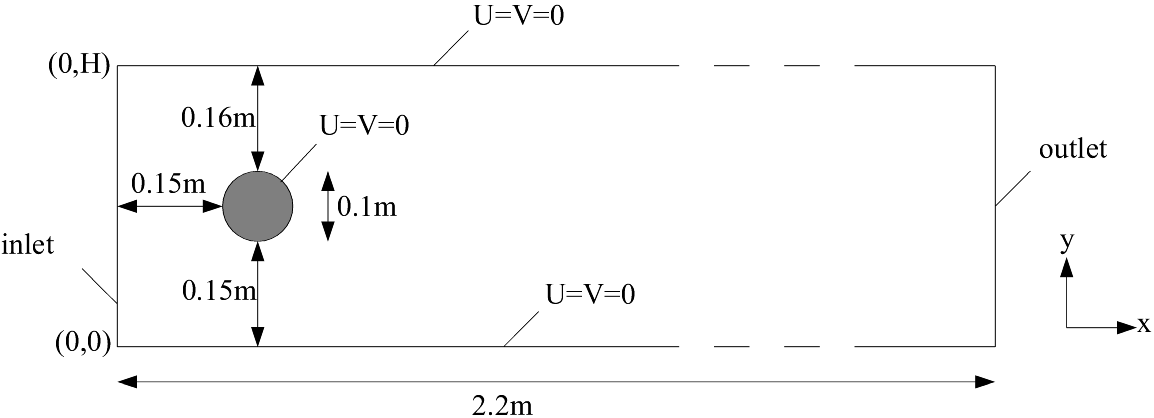
Avec un adimensionnement correct (si l'on tient compte de l'invariance galiléenne entre autre) nous avons
besoin approximativement d'un site par millimètre carré, soit 2200*410=902000 sites ou environ
1 mégaoctet. Les PC actuels disposent d'au moins 64 Mo actuellement et le calcul à 1Mc/s permet
de soutenir un affichage à 1Hz dans ce cas. Dans des conditions
idéales (densité, vitesse...), nous pouvons donc très facilement atteindre le nombre de
Reynolds requis par le benchmark. Il reste ensuite assez de marge pour corriger les artifacts du réseau.
Les allées de von Karman ont été simulées par plusieurs laboratoires, dont les laboratoires Fuji (Japon),
l'Université Libre de Bruxelles,
l'Université de Munich
ou l'Observatoire de Nice pour citer quelques exemples.
Dans la comparaison suivante, nous étudions la différence entre une résolution temporelle d'équations
classiques et un calcul FHP-3 :
Dans des conditions appropriées et avec l'adimensionnement correct, les résultats sont similaires. Toutefois,
les gaz sur réseaux permettent de faire apparaître les fluctuations dûes au mouvement brownien. La simulation
est donc bruitée et nécessite une intégration temporelle et spatiale pour effectuer une mesure. Cependant, l'apparition
de phénomènes complexes est naturelle et n'a pas besoin d'être forcée (ou si peu) : le cercle du benchmark est
décalé d'un centimètre dans le tunnel (1/41=2,5%) alors que dans l'expérience FHP il n'est décalé que d'un pixel
(1/200=0,5%, mais cela est probablement involontaire et lié à l'algorithme de dessin du cercle).
D'habitude, le décentrage est nécessaire pour forcer l'apparition rapide des tourbillons contrarotatifs
car la méthode de résolution classique n'est pas bruitée par nature. La recherche d'une solution
exacte implique qu'une dissymétrie n'apparaitra qu'avec une erreur d'arrondi. En revanche, les gaz sur réseaux comme FHP
permettent au bruit brownien d'organiser les turbulences microscopiques (à l'échelle de quelques sites)
en turbulences macroscopiques (qui peuvent être étudiées par intégration sur de nombreux sites) et de faire apparaître
les allées caractéristiques sans forçage ou dissimétrie artificiels. De plus, la complexité de la géométrie du
tunnel est arbitraire et n'influence pas le calcul.
Le programme de David Hanon mélange par codage les parois glissantes et rugueuses. En raison de l'impératif
du changement dynamique de la géométrie du tunnel, cette approche devient complexe et il faut pouvoir gérer
des parois de toute nature dans notre code final.
III.10 : Conclusion :
Les deux codes de référence, ainsi que les nombreuses versions intermédiaires et les expériences
qu'ils ont permis de conduire, montrent que le niveau de performance espéré ne peut être atteint
qu'avec des techniques de codage et des algorithmes plus sophistiqués. L'approche par
lookup table a atteint ses limites car il n'est pas possible de diminuer le nombre
d'instructions par noeuds à cause des limitations et des contraintes architecturales (pas assez
de registres, mode réel ou unreal trop limités, préfixes divers et mémoire lente).
L'apparition vers 1997 du jeu d'instructions MMX ainsi que la lecture plus attentive
du livre de Michael Abrash [7] renforcent la conviction qu'il faut
revoir le programme depuis le début.
Partie IV : Réalisation
IV.1 Introduction :
Les premiers programmes de LGA sont relativement petits (le kernel comprend moins de 100 instructions)
et commencent déjà à nécessiter une attention soutenue pour fonctionner correctement. Le temps nécessaire à mettre
un programme au point se mesure en semaines puis en mois pour la version en assembleur. Le projet décrit ici est encore
plus ambitieux et nécessite une longue préparation pour que tous les éléments puissent fonctionner correctement, d'abord
seuls puis en coopération avec les autres. Il faut concevoir chaque élément indépendemment tout en prévoyant leur
assemblage final, il est donc nécessaire d'avoir une vue générale du projet aussi claire que possible.
Ce projet a été lancé au départ car il a été préparé pendant plusieurs années : la plateforme est mieux maitrisée
(en particulier le développement en assembleur MMX en mode protégé) et l'algorithme de strip mining
est imaginé. Certains autres aspects algorithmiques et structurels sont imaginés comme l'organisation des données
et la représentation des parois. En théorie, le projet ne devrait pas être compliqué mais "le démon se cache
toujours dans les détails"...
IV.2 : Intel : la plateforme idéale malgré elle
Pour les nombreuses raisons exposées précédemment, la plateforme reste le PC sous MS-DOS. De plus, le
développement dans un autre environnement et à ce niveau nécessiterait l'apprentissage d'autres
techniques et MS-DOS est le seul environnement permettant un contrôle total de la machine,
condition nécessaire pour trouver les goulots d'étranglement des algorithmes testés, sans interférences
du système d'exploitation ni d'événements extérieurs incontrôlables. Enfin, bien que l'avenir commercial
de ce système soit incertain, des alternatives libres comme FreeDOS permettront de distribuer le
programme avec le système d'exploitation préconfiguré, afin d'en simplifier l'utilisation et la
diffusion gratuite. Il n'est pas question d'utiliser d'ALPHA, de SPARC ou de PowerPC malgré leur
puissance supérieure. Un CRAY (T3E ou SV) conviendrait très bien car les outils de profiling sont
livrés mais outre le prix et la place déraisonnables, le but du projet n'est pas d'atteindre
la plus haute performance possible mais bien de trouver des techniques afin de mieux exploiter
une machine existante et facilement disponible. Le défi algorithmique est déjà suffisamment
complexe.
Avec le temps, de nouveaux processeurs Intel et clones sont apparus : récemment l'Athlon d'AMD a
surpassé le PIII d'Intel (voir "la Jihad
des CPU de 7ème génération" par Paul Hsieh) et les compagnies se font une concurrence frénétique,
au niveau des prix, de la performance et des fonctionalités, pour la maîtrise du
marché. Pour des raisons pratiques, nous devons nous concentrer sur une partie seulement des
architectures disponibles, en espérant que les autres architectures ne soient pas complétement
différentes. La compatibilité binaire entre les versions garantit cependant que le programme
fonctionne partout où les fonctions nécessaires (souris série, VESA2, MMX, MS-DOS et HIMEM.SYS
en mode réel) sont présentes.
Nous allons nous concentrer sur deux processeurs et leur architecture : le Pentium MMX à 200MHz,
disponible à la maison, et le Pentium II dont plusieurs sont disponibles à l'université, dont deux
en version biprocesseur. Ce sont deux architectures répandues et connues, mais suffisamment
différentes pour nécessiter une étude particulière. Le premier (P200MMX) est un processeur
superscalaire à deux voies, proche d'un RISC classique, alors que le deuxième (PII) a un
coeur OOO (Out Of Order execution) pouvant traiter 40 instructions à différents stades
de leur exécution, disposant de 80 registres renommés. L'interface avec la mémoire centrale et la
"résistance à la charge de calcul" sont complétement différentes et nécessiteraient deux versions
différentes du programme : le P200MMX est un processeur "statique", qui reste assez prévisible grâce
à sa cache d'instructions, alors que le PII est entièrement dynamique et non déterministe ! Pour ne
rien améliorer, les règles de codage sont radicalement différentes. Les schémas ci-dessous illustrent
les différences architecturales entre les deux types de processeurs :
courtesy of Intel
De nombreuses ressources sont disponibles, notamment dans la bibliographie et sur Internet. Michael Abrash
[7] décrit bien les aspects importants de la programmation du Pentium classique et
l'adjonction du jeu d'instruction MMX est relativement simple :
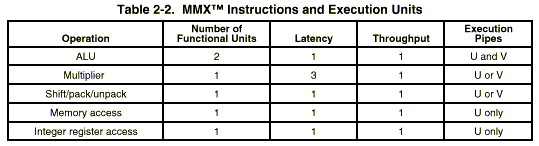 Par contre, les règles de codage pour le PII (qui est un Pentium Pro avec support du jeu d'instructions MMX) sont différentes
et dépendent de l'architecture remodelée du coeur OOO : ce processeur travaille en transformant les instruction
x86 en µops, ce qui modifie les règles de groupement des instructions. Nous reviendrons bientôt
sur ce problème.
Par contre, les règles de codage pour le PII (qui est un Pentium Pro avec support du jeu d'instructions MMX) sont différentes
et dépendent de l'architecture remodelée du coeur OOO : ce processeur travaille en transformant les instruction
x86 en µops, ce qui modifie les règles de groupement des instructions. Nous reviendrons bientôt
sur ce problème.
Le DOS-Extender (ou "loader 32 bits") est un morceau de code situé au début d'un programme MS-DOS
autonome et qui place le processeur en mode 32 bits : il permet ainsi d'utiliser les registres sur 32 bits sans
utiliser de préfixe de taille, donc de faire fonctionner le programme plus vite. Son développement a commencé vers
1997 et s'est stabilisé rapidement car il est court et conçu pour être très compact : le
code binaire occupe moins d'un kilo-octet.
Le mode DPMI (DOS Protected Mode Interface) permettant d'utiliser le mode protégé 32 bits sous Windows a été
essayé mais de nombreuses difficultés ont empêché de poursuivre l'effort dans cette direction : il a été
plus simple de tout recoder à la main car cela évite d'être dépendant de conventions et d'interfaces complexes,
contraignantes et inadaptées. Le loader est minimal et ne remplit que les fonctions nécessaires.
Il a d'abord été programmé avec TASM mais le mélange des codes
16 bits et 32 bits a rendu le codage très difficile. Il a été porté très facilement sous NASM et ce sera l'assembleur
final : il est distribué sous GPL, il est de plus en plus utilisé, il est stable et
surtout sa syntaxe est très simple et très pratique, débarrassée de toute convention inutile.
L'utilisation des directives USE16 et USE32 a fait disparaître de nombreuses
difficultés qui ont freiné le développement avec TASM, en particulier l'adjonction manuelle
des préfixes de taille ("db 66h" et "db 67h"). Pour compléter, j'ai écrit un
ensemble de fonctions permettant de se passer d'un linker et qui permet de générer
l'entête d'un fichier EXE. Ces fonctions font actuellement partie de la bibliothèque de macros de NASM.
Enfin, deux programmes (une sorte de préprocesseur et un patcheur d'entête) écrits en Turbo Pascal
fournissent les derniers utilitaires pour programmer sans se préoccuper de certains détails de bas
niveau.
Une fois le programme lancé, nous disposons de l'environnement idéal : nous pouvons accéder linéairement
à 64Mo (limite du standard XMS) en nous souciant beaucoup moins des segments qu'avant. Seules trois
interruptions sont utilisées : le clavier, la souris et la procédure d'erreur fatale (qui est déclenchée
par le processeur lorsqu'un bug se manifeste violemment). Ainsi, il n'y a pas un seul cycle que nous
ne pouvons contrôler et nous disposons de l'intégralité de la puissance de la machine, sans autre
entrave que son architecture. Cet environnement est augmenté de fonctions au fur et à mesure que leur
intégration devient possible. Par exemple, une fois que le contrôle de la carte vidéo en mode
1024*768*256/LFB est assuré, la souris est intégrée pour entrer des ordres. Presque toutes les
fonctions sont testées hors de l'environnement avant d'être intégrées, souvent en langage Turbo Pascal
pour faciliter le débogage et la compréhension des algorithmes. Par exemple, voici le
programme qui est à la base du driver de souris :
Uses Crt, Dos;
{$F+}
const COM1INTR = $0C;
COM1PORT = $3F8;
var bytenum : word;
combytes : array[0..2] of byte;
x, y : longint;
button1, button2,changed : boolean;
MouseHandler : procedure;
procedure MyMouseHandler; Interrupt;
var dx, dy : integer;
var inbyte : byte;
begin
inbyte := Port[COM1PORT]; { Get the port byte }
{ Make sure we are properly "synched" }
if (inbyte and 64) = 64 then bytenum := 0;
{ Store the byte and adjust bytenum }
combytes[bytenum] := inbyte;
inc(bytenum);
{ Have we received all 3 bytes? }
if bytenum = 3 then
begin
{ Yes, so process them }
dx := (combytes[0] and 3) shl 6 + combytes[1];
dy := (combytes[0] and 12) shl 4 + combytes[2];
if dx >= 128 then dx := dx - 256;
if dy >= 128 then dy := dy - 256;
x := x + dx;
y := y + dy;
button1 := (combytes[0] And 32) <> 0;
button2 := (combytes[0] And 16) <> 0;
{ And start on first byte again }
bytenum := 0;
changed := true;
end;
{ Acknowledge the interrupt }
Port[$20] := $20;
end;
|
var error: boolean;
begin
ClrScr;
error:=false;
{ Initialize the normal mouse handler }
asm
mov ax, 0
int $33
inc ax
jne @the_end
mov ax,24h
int 33h { get mouse parameters }
inc ax
je @the_end { no mouse or other error }
cmp ch,2
jne @the_end { we want a serial mouse }
cmp cl,2 { COM port }
jae @not_the_end
@the_end:
mov word ptr [error], -1
@not_the_end:
end;
if error then halt(1);
{ Initialize some of the variables we'll be using }
bytenum := 0;
x := 0;
y := 0;
button1 := false;
button2 := false;
{ Save the current mouse handler and set up our own }
GetIntVec(COM1INTR, @MouseHandler);
SetIntVec(COM1INTR, Addr(MyMouseHandler));
while not keypressed do
if changed then
begin
WriteLn(x : 5, y : 5, button1 : 7, button2 : 7);
changed:=false;
end;
SetIntVec(COM1INTR, @MouseHandler);
end.
|
Une fois l'algorithme compris, le code est traduit en langage assembleur et retesté avec Turbo Pascal
en inline. Ensuite, la partie développée et validée peut être recopiée dans l'environnement
en assembleur, après une légère traduction de la syntaxe (Turbo Pascal -> NASM) et le renommage
des variables. C'est à cet endoit que surviennent la plupart des problèmes : faute de frappe,
erreur de copier/coller, syntaxe erronnée mais non détectée par NASM ... Les problèmes sont facilement
éliminés avec beaucoup de pratique, de méthode et de patience et les cas simples permettent de
se préparer aux cas très difficiles. Par exemple, certains bugs ont nécessité deux semaines pour
être résolus alors qu'un module peut être intégré en quelques heures : la programmation est un exercice
non linéaire ! Le type de code précédent n'a pas été optimisé très fortement : son exécution n'est pas
absolument critique et l'accès aux entrées-sorties prend la plupart des cycles. Il a donc été recodé pour
être le plus compact possible et effectuer seulement les opérations nécessaires, grâce
à de nombreux paramètres pré-codés ou définis une fois pour toute (comme le curseur de la souris).
A ce niveau, cela suffit pour atteindre l'objectif de performance désiré.
Lorsque le code le permettait, un stub a été intégré pour supporter les plateformes
bi-processeur. Cela a demandé trois jours non-stop de travail pour lire les documents d'Intel
mais le résultat est simple, compact et bien cerné. La communication s'effectue simplement
avec des sémaphores en mémoire.
Le système de cohérence de caches MESI a été mis à l'épreuve et des mesures ont montré
que cette plateforme n'est intéressante que pour des applications CPU bound (les deux processeurs
à 266 MHz doivent se partager un unique bus similaire à celui du Pentium 100). Toutefois, après quelques
mois d'utilisation, le stub a été dévalidé afin de pouvoir se concentrer sur la partie la plus importante :
le calcul. En effet, il faut programmer une version mono- et bi-processeur pour chaque version du kernel
de calcul et cela ralentit le développement. Le code bi-processeur reste toujours disponible et la
structure du programme est préservée pour permettre son retour lorsque le code sera abouti et parallélisable.
IV.3 : Description de l'algorithme de strip mining
Comme nous l'avons constaté avec les programmes de la partie III,
la bande passante avec la mémoire est une "ressource" très importante
car elle peut faire ralentir le programme d'une manière dramatique. Le deuxième code de référence ne résoud
pas tout à fait le problème car la vitesse de calcul est inversement proportionnelle à la vitesse de l'affichage
et il faut donc choisir entre interactivité et temps de calcul. Le choix de l'algorithme est mieux adapté
au Pentium que pour le premier exemple destiné au i286 mais l'affichage hors de la boucle de calcul est une
erreur stratégique car elle génère autant de cache misses que le calcul. L'affichage entrelacé avec
le calcul réduirait le nombre de cache misses, améliorerait la vitesse de rendu à l'écran et bénéficierait
naturellement de la localité spatiale et temporelle.
|
Cependant, la situation va encore se détériorer dans l'avenir car malgré les lourds investissements
réalisés dans ce domaine par les industriels, la bande passante vers la mémoire centrale s'accroît
plus lentement que la vitesse de traitement des processeurs. Si notre algorithme est basé sur un
balayage linéaire de toute la mémoire, l'accélération réalisée en utilisant une plateforme
"plus rapide" ne sera pas proportionnelle à l'augmentation de la vitesse du processeur.
L'entrelacement de l'affichage avec le calcul, nécessaire pour réduire le nombre
de transactions sur le bus mémoire, n'est pas suffisant pour permettre à l'algorithme d'exploiter
les plateformes modernes et celles qui leur succèderont : nous serons toujours limités par la vitesse
d'accès à la mémoire centrale, accédée en lecture et en écriture.
| 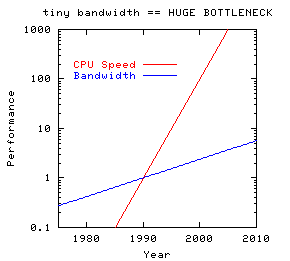
extrait de la page d'accueil du benchmark STREAM |
Pour traiter un tableau de N sites, il faudra donc accéder à N*2
sites ainsi qu'à la mémoire vidéo ce qui sature tragiquement le bus mémoire. Si le problème est
lié au balayage linéaire, il faut alors y renoncer. Il faut balayer d'une manière qui
permette à la mémoire cache d'être utilisée de manière optimale, c'est à dire :
extraire la localité spatiale et temporelle du modèle. Nous devons pour cela analyser
la dépendance des données à chaque pas de temps entre une cellule et ses voisins :
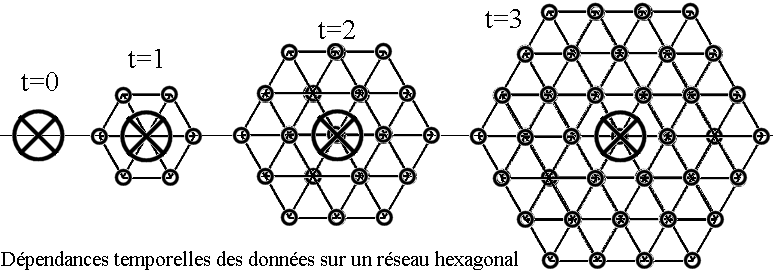 Nous voyons sur le schéma précédent que si nous partons du calcul d'une cellule, le pas de temps suivant
fera intervenir 6 cellules supplémentaires, 12 cellules puis 18 cellules pour chaque pas de temps
successif et ainsi de suite. Commencer le calcul à partir d'une seule cellule se traduit par une croissance
hexagonale du domaine à traiter. Le voisinage hexagonal impose des manipulations de données
complexes, masquages et décalages, nécessaires au traitement exclusif des cellules qui nous
concernent pour chaque étape, ce qui réduit l'efficacité du programme. Nous ne pouvons pas
nous baser directement sur le voisinage pour créer un nouveau balayage.
Nous voyons sur le schéma précédent que si nous partons du calcul d'une cellule, le pas de temps suivant
fera intervenir 6 cellules supplémentaires, 12 cellules puis 18 cellules pour chaque pas de temps
successif et ainsi de suite. Commencer le calcul à partir d'une seule cellule se traduit par une croissance
hexagonale du domaine à traiter. Le voisinage hexagonal impose des manipulations de données
complexes, masquages et décalages, nécessaires au traitement exclusif des cellules qui nous
concernent pour chaque étape, ce qui réduit l'efficacité du programme. Nous ne pouvons pas
nous baser directement sur le voisinage pour créer un nouveau balayage.
Le problème est simplifié si l'on s'inspire d'une technique qui traite des lignes au lieu
de cellules individuelles : la dépendance des données se confond alors dans une croissance
linéaire, non hexagonale, du domaine à traiter. La technique de strip mining est connue
et principalement utilisée sur des plateformes sophistiquées, multi-processeurs, avec plusieurs
niveaux de mémoire, c'est à dire où l'accès à la mémoire n'est pas uniforme, comme dans notre cas.
Le principe de cette technique est de diviser le domaine calculé en bandes (strips) et de
les balayer de manière non linéaire. Par exemple, en utilisant des propriétés mathématiques,
il est possible de réorganiser les données d'une matrice afin de calculer son inverse :
le programme de strip mining ne balaiera plus les données de manière triviale et les données
resteront plus longtemps en mémoire cache, ce qui accélère le calcul. Dans notre cas, ce ne
sont pas des propriétés mathématiques mais géométriques qu'il faut étudier.
Nos strips correspondront aux lignes du tableau : elles seront calculées par
une boucle simple, en distingant toutefois les lignes paires et impaires (comme pour le premier
code de référence). Les lignes sont ensuite balayées à un niveau supérieur avec une "fenêtre
glissante" : c'est un balayage similaire à une double boucle imbriquée, portant sur l'axe y.
L'algorithme de balayage consiste donc en trois boucles les unes dans les autres :
for y:=0 to y_max do (* balayage général : génère les cache misses *)
begin
for i:=0 to strip do (* boucle interne de strip mining, sans inclure l'amroçage *)
for x:=0 to x_max do (* balayage d'un strip *)
calcule (x,y+i); (* le débordement en y n'est pas traité dans ce pseudo-code *)
affiche_ligne(y);
end; |
Nous pouvons voir que cette adaptation convient aux nécessités de l'affichage, sans que la cache
ne soit vidée : le transfert des données vers l'extérieur s'effectue avec la garantie
que les données soient déjà en cache si le paramètre strip est bien choisi.
La bande passante du bus externe du processeur est donc divisée en 3 : lecture, écriture
des éléments modifiés, affichage.
Cependant les éléments mis en jeu sont très complexes : ce balayage composé implique que
l'on peut trouver sur le tableau, lors du calcul, des sites dont les valeurs correspondent à
des pas de temps éloignés, il faut un mécanisme adapté pour gérer les buffers nécessaires.
Le schéma suivant montre les dépendances sur l'axe y à tous les pas intermédiaires
du calcul d'un tableau de 7 lignes et avec un strip mining de 3 lignes :
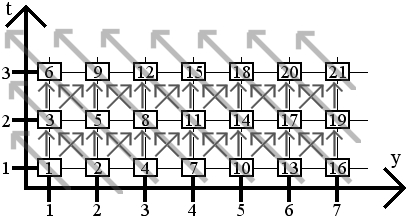 |
Le sens de balayage global est sur l'axe y, le sens de balayage de la boucle
interne est symbolisé par les larges flèches transparentes. Les cases représentent différentes
valeurs pour chaque ligne à différentes étapes, elles sont numérotées dans l'ordre
d'appel de la fonction de calcul. Les petites flèches montrent les dépendances
de données entre les cellules.
|
Nous pouvons apercevoir que le cas de buffer temporaire expliqué en
partie III.3 est un cas particulier de ce nouvel algorithme lorsque
strip est égal à 1. Cela signifie que le plan temporaire dans ce cas particulier ne change pas.
Par contre, lorsque strip augmente, la gestion du plan temporaire devient beaucoup plus complexe :
il faut strip lignes de buffer et autant de pas de temps différents sont
présents sur le tableau. Le déplacement des données dans le tableau demande alors encore plus
de soin lors du développement et nécessite une préparation importante. La réalisation du programme
a été plus difficile que prévu, principalement car l'algorithme de balayage initialement utilisé comportait
des dépendances spatio-temporelles cachées qui étaient impossibles à résoudre sans une révision complète
du programme.
Dans le programme final, tous les indices sont transformés en pointeurs et linéarisés afin
de réduire à la fois le nombre nécessaire de registres et le nombres d'instructions de calcul.
La structure de boucle présentée initialement ne convient pas pour gérer l'amorçage
du buffer de strip mining : nous avons vu que le balayage doit commencer et se terminer
en augmentant puis en réduisant progressivement le nombre de strips.
La fenêtre de calcul est alors cernée par deux pointeurs, modifiés par de simples opérations
de comparaison/assignement. La boucle est ainsi contrôlée par des conditions complexes
mais le nombre de paramètres est réduit à deux variables : "début" et "fin".
"fin" est "poursuivi" par "début", la chasse se termine lorque "début" dépasse la "fin"
(c'est à dire : la fin du tunnel, mais pour réduire les dépendances entre les registres,
ce paramètre est confondu avec une valeur immédiate connue).
D'autres pointeurs sont aussi nécessaires pour gérer les tableaux temporaires.
const strip=2;
var buf:array[0..strip-1,0..159,0..1] of byte; (* buffer temporaire *)
var j,debut,fin,debut_buf:word;
label calcul;
begin
while not keypressed do
begin
debut:=1; (* initialisation des pointeurs *)
fin:=1;
debut_buf:=0;
calcul:
for j:=fin downto debut do
begin
if (j and 1)=1 then (* parité de la ligne *)
(* calcule une ligne impaire *)
else
(* calcule une ligne paire *)
end;
if fin=199 then
inc(debut_buf)
else
inc (fin);
if fin<strip+1 then
goto calcul;
(* affichage ligne ici *)
inc(debut);
if debut<=199 then
goto calcul;
end;
|
Cet algorithme des pointeurs qui se poursuivent a été adapté pour ne nécessiter qu'un
minimum de sauts et de structures if-then-else. Dans la version en assembleur,
les pointeurs sont en plus "linéarisés" : ils ne sont pas incrémentés de 1 mais augmentés
de la taille d'une ligne et augmentés par l'adresse du début du tunnel,
afin de pouvoir effectuer des comparaisons directes entre les pointeurs qui servent
aussi de compteurs. Toutefois, bien que la structure de strip mining externe soit assez simple,
les détails internes deviennent très complexes. En particulier, le "saut temporel", qui sépare les sites
entre le début et la fin de la fenêtre, agit comme un saut géométrique et nécessite donc un buffer
temporaire aussi gros que la fenêtre. La gestion des pointeurs à l'intérieur de cette structure est
difficile à mettre au point.
Les mésaventures dûes au strip mining sont nombreuses mais la plus importante met en jeu la structure
complète du programme. Nous avons vu dans les pseudo-codes précédents que nous pouvions profiter
de l'algorithme pour y inclure la fonction d'affichage. Le programme réalisé
va plus loin en essayant d'utiliser la structure du buffer temporaire pour mémoriser des informations sur
la fenêtre courante, en particulier afin d'effectuer une accumulation des particules et afficher la
densité dans le tunnel. L'avantage évident est que cela économise beaucoup de mémoire : le buffer
d'affichage nécessite alors strip lignes au lieu de y et cela nous ramène au cas décrit
pour le buffer temporaire simple (au total : y+1 lignes au lieu de 2y). Pourtant la
réalisation fait apparaître que les données
ne sont pas accédées dans le même ordre que pour le buffer temporaire de déplacement : l'affichage
nécessite un pointeur supplémentaire ainsi qu'un algortihme nouveau, même si la place occupée
n'est pas un problème. Tous les registres utilisables sont déjà alloués et l'accumulation de
données sur la fenêtre n'est pas possible. Seules les données
disponibles à un intervale de
strip pas de temps peuvent être affichées. Aussi, l'affichage sophistiqué
prévu au départ n'a pas été inclus dans le programme même s'il est déjà conçu et testé. A posteriori,
la technique simple (consommant beaucoup de mémoire) aurait été préférable mais la structure du
code existant est trop avancée et figée pour pouvoir être modifiée. Un recodage complet est nécessaire
et serait plus rapide.
Le speedup permis par l'algorithme de strip mining dépend du nombre de lignes contenues dans la
fenêtre et sa taille dépend de nombreux paramètres. Afin de maximiser la réutilisation des données,
il faut donc que la fenêtre corresponde le mieux possible aux caractéristiques de la mémoire de la machine,
ce qui est absolument indéterministe et imprévisible. La première mesure à prendre est d'orienter
le tableau dans la hauteur afin que la fenêtre soit la plus étroite possible. Par exemple, dans le cas des
allées de von Karman, il faut tourner le tunnel à 90 degrés (hauteur plus grande que la largeur) afin que
l'algorithme soit plus efficace. En effet, le speedup est proportionnel à strip, ce que
confirment les mesures. Pour le cas d'une version multiprocesseur, cela veut dire que le découpage
du domaine doit se faire dans la largeur afin de réduire la bande passante du bus externe,
même si cela augmente le nombre de sémaphores de synchronisation.
Ensuite, il faut que le nombre de lignes dans la fenêtre ne soit ni trop grand ni trop petit mais il
n'y a pas de formule générale permettant de déterminer ce paramètre. La solution la plus
efficace et la plus simple est de mesurer en conditions réelles toutes les possibilités :
c'est l'étape de calibration qui calcule plusieurs pas de temps et mesure le temps pour chaque
largeur de la fenêtre. A la fin des mesures, il détermine le meilleur score (le temps divisé par
la taille de la fenêtre) : le résultat, en nombre de lignes, servira pour
les calculs futurs. La calibration doit être effectuée à chaque fois que les paramètres de simulation
changent (nombre de sites ou géométrie du tunnel) afin que le temps de calcul soit toujours optimal.
Pour des raisons historiques et pratiques, la recherche exhaustive est limitée à 32 valeurs
de strip mais il n'est pas nécessaire d'augmenter ce nombre et cela suffit pour de donner une
bonne idée sur l'architecture de la mémoire
de la machine. Par des mesures, calculs et déductions, il est possible de déterminer la bande passante
réelle de la mémoire centrale ou la taille de la mémoire cache. Les processeurs les plus récents
(Pentium II par exemple) ont une excellente réponse au strip mining, utilisant souvent un nombre maximal
de lignes dans la fenêtre, alors que les processeurs de cinquième génération avec cache L2 externe
ont un score faible correspondant à la taille de la mémoire cache L1.
A première vue, le strip mining est une technique complexe dont l'efficacité n'est pas garantie :
le gain en performance est dépendant de l'architecture de la machine et sa complexité pratique est peu
évidente à appréhender. Toutefois c'est un algorithme adaptatif qui ne surcharge pas la machine
lorsque c'est inutile et son efficacité est démontrée en pratique pour les plateformes actuelles.
Nous allons voir à la fin de cette partie une application réelle où le speedup approche 2,5.
Dans le cas qui nous concerne, le strip mining utilisé ici est une version très spéciale adaptée aux
tableaux en deux dimensions. Son extension à d'autres dimensions est envisageable mais sa complexité
intrinsèque doit être complétement maitrisée : les mésaventures avec la version actuelle du code (en
particulier les croisements de pointeurs pour l'affichage) montrent que ce domaine particulier devrait être
étudié plus
en profondeur de manière "académique" pour être connu et utilisé largement. Le manque de connaissances
préliminaires a rendu la programmation difficile, malgré la longue préparation. Espérons que dans le
futur, cet algorithme sera mieux étudié et se banalisera car c'est une solution simple et non calculatoire
(indépendante du "Grand O") pour accélérer les calculs lourds sur les machines actuelles et futures.
IV.4 : Nouvelle structure des données et méthode de calcul
Nous avons vu que même en groupant les octets par 4, il faut toujours
47 instructions de mouvement des données contre 12 pour la consultation de la table :
le premier programme nécessitait 30 instructions de mouvement pour 6 de consultation,
nous sommes passés de 5:1 à 4:1 avec une augmentation de la taille du code de 1,6.
Il est clair que pour accélérer le programme, il faut réduire le temps passé à bouger les bits.
En ignorant les autres paramètres, il faudrait diviser par quatre le nombre d'instructions de mouvement
de données pour doubler la vitesse de calcul. Malheureusement nous ne pouvons pas agir sur le jeu
d'instructions, nous devons jouer sur l'organisation des données pour réduire cet énorme problème.
Si le programme passe les 4/5èmes de son temps à bouger les bits, c'est parcequ'il doit extraire
puis insérer des bits dans d'autres mots (le processeur ne dispose pas d'instruction spéciale pour cette
tâche), ceci sept fois par site, pour tous les sites. Nous devons donc utiliser une représentation
des données qui réduit au maximum le nombre d'instructions nécessaires au mouvement. La structure
la plus simple est évidemment le mot long, permettant en MMX de coder 64 particules allant dans
la même direction.
Le calcul est un nouveau problème : il faut l'effectuer par opérations logiques explicites au lieu
de consulter des tables. Nous ne disposons pas d'instruction adéquate permettant de transformer
7 mots de 64 bits en 64 octets. Le problème est toutefois plus compliqué car l'enjeu est de pouvoir
suivre la croissance de la puissance des ordinateur et cette croissance passe par l'augmentation
de la largeur des mots : les programmes consultant des tables sont donc condamnés à stagner au niveau
de la performance car le nombre de sites calculés restera proportionnel au nombre
de consultations. Au contraire, en utilisant une technique basée sur la représentation parallèle
des sites, une augmentation de la largeur des mots augmentera la vitesse de calcul. Une estimation
situe le "point de rupture" à des mots de 32 bits : cette technique n'est pas intéressante pour
un processeur 16 bits mais cela dépend aussi beaucoup du nombre de registres, du jeu d'instructions
et du nombre d'instructions décodées par cycle. L'introduction des instructions MMX et les registres
associés favorisent beaucoup l'utilisation du modèle à calcul explicite, malgré la complexité inhérente
du programme.
L'organisation des données au niveau macroscopique joue aussi un rôle important. Traditionnellement,
la technique "multi-spin" (en référence au modèle d'Ising) regroupe les sept directions dans sept
tableaux car les ordinateurs vectoriels (CRAY surtout) peuvent traiter 4096 sites en une seule instruction
(8 registres vectoriels de 64 fois 64 bits). Ce type d'organisation perdure encore dans les habitudes
mais se heurte comme les autres algorithmes aux architectures complexes des microprocesseurs récents. Par
exemple, il faut 7 pointeurs pour désigner le tableau d'origine et 7 pointeurs pour le tableau de destination
(en utilisant l'organisation simple, sans buffer temporaire) et les CRAY (comme la plupart des autres
processeurs courants) n'ont que 8 registres d'adresse. Ensuite, la mémoire cache, ajoutée au processeur
pour pallier au manque de bande passante avec la mémoire centrale, crée des problèmes d'associativité
d'ensemble : pour le Pentium par exemple (8Ko associatif à 2 voies) des accès consécutifs à des adresses
identiques modulo 4096 provoquent de nombreux cache misses artificiels. Nous voyons encore ici que les
algorithmes, même si leur programmation semble facile, survivent mal aux évolutions de la plateforme.
L'organisation que nous allons utiliser maintenant est un compromis entre "multi-spin" et "multi-site" :
la première contrainte est de diminuer au maximum le nombre de registres pointeurs nécessaires. Il faut
donc "linéariser" les accès et limiter les modes d'adressage au mode
registre + index immédiat. Pour réduire encore plus le nombre
de registres inutilement utilisés dans le kernel, l'index sera parfois modifié à la volée
par du code automodifiant, par exemple pour l'accès à des cellules d'une ligne différente.
Le code automodifiant est évidemment placé hors de la boucle et n'est utilisé que lorsque
la taille du tableau change, pour éviter les lourdes pénalités à la première exécution.
/* quelques définitions : */
#define max_x 512
#define max_y 512
#define lli long long int
#define slli (sizeof(long long int))
/* déclaration en C d'un tableau multi-site : */
char tableau[max_y][max_x];
(comme pour les programmes étudiés jusqu'ici)
/* déclaration en C d'un tableau multi-spin : */
lli a[max_y][max_y/slli];
lli b[max_y][max_y/slli];
lli c[max_y][max_y/slli];
lli d[max_y][max_y/slli];
lli e[max_y][max_y/slli];
lli f[max_y][max_y/slli];
lli g[max_y][max_y/slli];
(pour les ordinateurs vectoriels)
/* déclaration en C d'un tableau composite : */
struct site {
lli a,b,c,d,e,f,g;
} tableau[max_y][max_y/slli];
|
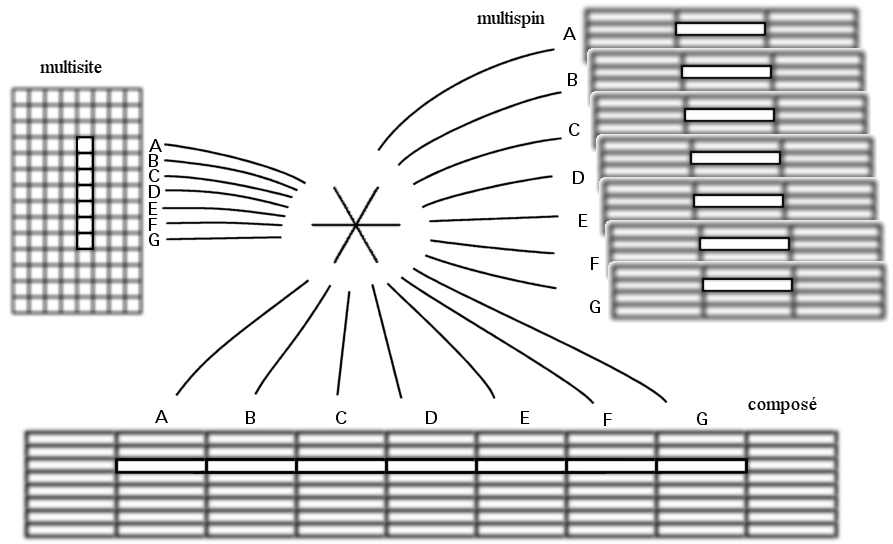
L'annexe D présente différentes variations des structures de données
qui ont été programmées. Comme ces logiciels sont écrits en langage de haut niveau, les contraintes
de performance sont difficilement visibles au niveau du code source. De plus, la complexité croissante
des plateformes n'est pas le souci majeur des programmeurs dont le seul but est d'obtenir un résultat
valide. La structure composite n'est donc pas encore répandue dans les codes FHP et la
dénomination officielle n'existe pas encore, cette organisation peut aussi bien être appelée
multispin entrelacé.
IV.5 : Implémentation des parois
La nouvelle organisation des données permet à la fois d'économiser de la bande passante vers
la mémoire et de créer des parois plus flexibles mais, comme dans le reste du projet,
aux dépends de la complexité du code et du temps de développement.
Tout d'abord, il faut remarquer la limitation inhérente aux parois
"rugueuses" telles que programmées
dans les programmes précédents où un seul bit était utilisé. D'un côté, les parois sont très
faciles à gérer car il suffit de mettre un bit à 1 au bon endroit pour créer un mur.
De l'autre côté, moins d'un de ces bits sur cent est utilisé en pratique : nous pouvons donc gagner
facilement un huitième de bande passante en ne transmettant pas ce bit, car maintenant il est découplé
du domaine des particules.
|
Ensuite, le modèle à un bit est limité par le type de parois qu'il peut implémenter :
nous avons vu que les parois rugueuses sont nécessaires mais insuffisantes dans les cas généraux.
Pourtant, le modèle FHP permet une plus grande variété d'orientation des parois. Même si pour un site,
une particule peut repartir dans 5 directions différentes lors d'un choc avec une paroi,
le nombre réel est de 12 directions de parois, c'est à dire une précision de 30 degrés.
Nous avons donc intérêt à réutiliser la bande passante gagnée pour trouver une autre représentation
des parois, qui permettrait par exemple de représenter une sphère lisse.
|
|
La structure et l'algorithme nécessaires à l'implémentation des parois est assez simple pour
la partie calcul mais cette facilité est largement compensée par la complexité nécessaire
à la fabrication des données représentant les parois. Il suffit d'environ 20 instructions
pour dévier jusqu'à 128 particules de leur trajectoire grâce à un échange contrôlé par un
masque et deux pointeurs logés dans une structure de type mur. Ces pointeurs et ce masque
nécessitent cependant un mécanisme sophistiqué
pour être mis en place. Pour le programme de calcul, les parois sont "interprétées" grâce à
une sorte de liste chainée en mémoire. Son adresse de départ est fournie par un pointeur
de 32 bits logé dans la structure de type site qui devient donc :
/* déclaration en C d'un élément de liste de modification : */
typdef struct {
long int cpt; /* nombre d'éléments à interpréter */
short int offset1, offset2; /* pointeurs relatifs au site courant */
lli masque;
} mur;
/* déclaration en C d'un tableau composite : */
struct site {
lli a,b,c,d,e,f,g;
mur * liste;
long int pad; /* pour aligner la structure sur 8*64 bits */
} tableau[max_y][max_y/slli]; |
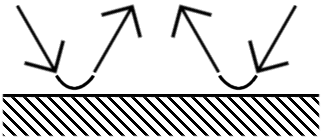
Dans la pratique, seuls les murs verticaux et horizontaux sont utilisés : les parois
obliques ou non rectilignes posent des problèmes à cause de la parité des lignes. En effet,
cela décale les parois d'un quart d'unité d'un côté ou de l'autre et l'algorithme
de Bresenham ou de différences finies numérique ne peuvent être utilisés directement.
Toutefois ce n'est pas
le problème le plus important : la programmation de l'algorithme de génération automatique
des listes de modifications est beaucoup plus complexe que lorsqu'on génère les listes
à la main comme lors des premiers essais. Les parois sont mémorisées sous forme de coordonnées
vectorielles et leur transformation en listes de modifications n'est pas évidente. Des difficultés
supplémentaires concernent l'efficacité de la transformation (format vectoriel->listes de modification,
qui doit donner un résultat le plus compact possible) et les croisements entre des parois
d'inclinaison différentes. Ces deux problèmes ont été traités mais celui de l'efficacité
n'est pas considéré comme résolu, en l'absence de preuves formelles d'optimalité. Quant au
croisement de parois aux orientantions différentes, le problème est résolu pour l'instant en
fabricant un "point chaud" : il faut créer un mur ponctuel aux parois non glissantes, sinon des
particules peuvent disparaitre dans l'interstice situé à l'intersection des parois.
| 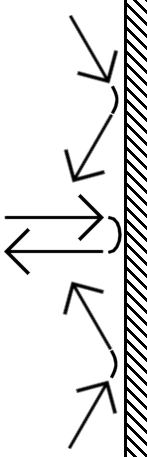
|
L'algorithme de transformation a été scindé en deux parties afin de séparer les difficultés.
La première partie est un petit interprète de données vectorielles. Seules les parois
lisses horizontales et verticales sont traitées pour l'instant : le codage de murs obliques ou
plus complexes est laissé comme exercice pour les curieux ou courageux qui en auront besoin.
Les coordonnées sont au format entier fractionnaire, codé sur 16 bits. Il suffit de les multiplier
par la taille du tunnel et de ne garder que les 16 bits supérieurs pour obtenir les coordonnées
réelles dans le tableau. Dans cette première partie, il faut décoder les vecteurs, vérifier
leur validité, puis les balayer sur toute leur longueur en appelant à chaque pixel la procédure
de la deuxième partie. Celle-ci attend les coordonnées d'un site ainsi que l'index des directions
à échanger.
Au fur et à mesure des appels, la deuxième partie va construire un réseau de structures
en essayant de réutiliser au maximum celles déjà construites, tout en évitant que des intersections
ne laissent échapper des particules. C'est un algorithme qui fonctionne bien, mais dont l'activité
est difficile à contrôler pour vérifier son efficacité. De plus, l'algorithme en Pascal prend
beaucoup de place et a été difficile à traduire en assembleur car il est difficile justement
de "voir" ce que l'algorithme fait, en plus des habituelles erreurs de fatigue et de frappe.
Toutefois, son fonctionnement satisfaisant prouve que le programme est possible
et il a permis de dégager les contraintes inhérentes au modèle. Un post-processeur, balayant
les structures créées, devrait permettre de les comprimer encore plus en éliminant celles
qui ne seraient plus utilisées : l'algorithme actuel n'est pas parfait et souffre de
memory leaks. Une étude à un plus haut niveau et l'utilisation de techniques plus
efficaces (étude et allocation globale des ressources) devraient permettre de générer des listes
optimales et ainsi de consommer moins de mémoire cache. Une autre possibilité serait de
compiler les structures de modifications au lieu d'interpréter des listes
L'objectif d'agrandissement arbitraire du tableau est preque atteint car les parois
peuvent être complétement redimensionnées dynamiquement. Il reste par contre à trouver
un bon algorithme pour le redimensionnement des masses de particules, mais cela ne sera
nécessaire que lorsqu'il sera possible de créer et de détruire des particules afin de
générer du vent dans le tableau. Un algorithme similaire à celui des listes de modifications
serait probablement utilisé.
IV.6 Algorithme d'affichage
Non seulement le calcul des collisions est plus difficile qu'avec l'organisation multisite,
mais l'affichage pose des problèmes que l'on pourrait qualifier d'intéressants. Rappelons
que l'affichage s'effectue avec un octet par site, la couleur étant contrôlée par une palette
effectuant la traduction dans le DAC de la carte vidéo.
Dans les programmes précédents, le site est tout simplement envoyé vers la carte vidéo et
il suffit de modifier la palette pour faire apparaitre les éléments désirés, comme la densité
ou la direction des particules. L'affichage est direct et naturel. Maintenant, il faut transformer
les plans de bits en octets et le même type de problème qu'avant se pose : il faut réduire le
nombre total d'instructions ainsi que le nombre d'instructions par site. Pourtant les vieilles
habitudes de codage sont tenaces : si le programme devait être codé dans un langage de haut niveau,
sans prendre le temps de réfléchir, son efficacité serait faible. Par exemple, le code suivant
en C pour effectuer la translation a une complexité ("grand O") proportionnelle au nombre de sites
et ne profite pas de la largeur croissante des registres :
struct site {
lli a,b,c,d,e,f,g;
mur * liste;
graph *p;
} *s;
unsigned char c, *d=video;
int i;
/* ce pseudo-code transforme un site pointé par s
en 64 octets pour afficher la densité : */
for (i=0; i<64; i++) {
c= ((s->a >>i)&1) + ((s->b >>i)&1) + ((s->c >>i)&1)+ ((s->d >>i)&1)
+ ((s->e >>i)&1) + ((s->f >>i)&1) + ((s->g >>i)&1);
*(video++)=c;
} |
Remarquons en passant qu'un deuxième pointeur est inséré dans site pour remplacer le mot
servant à aligner la structure sur une frontière de 64 bits. Ce pointeur peut être utilisé pour afficher
des éléments graphiques dont les caractéristiques ne sont pas encore précises car le programme
correspondant n'a pas été implémenté. Il servira plus tard pour l'affichage des statistiques locales
par exemple.
Le premier gros défaut de ce code est l'accès par octet à la mémoire vidéo,
nous avons pourtant vu que cela ralentit considérablement le code qui souffrira au moins de 64
lourdes pénalités. Ensuite, ce code est complétement linéaire, il traite chaque bit de chaque site
indépendamment, comme lors du déplacement des bits lors du calcul en multisite. Cet algorithme
"simple" n'exploite pas le parallélisme permis par les mots très larges. De plus, nous verrons dans
le prochain chapitre que le code de calcul doit être précédé d'un code d'accumulation qui transforme
les 7 bits d'entrée en 3 bits sous forme de représentation binaire
classique (voir aussi le schéma principal et l'annexe C,
page 33, pour le code). La réutilisation de ces données temporaires réduit le corps de la boucle
interne de moitié :
for (i=0; i<64; i++) {
c= ((s0 >>i)&1) + (((s1 >>i)<<1)&1) + (((s2 >>i)<<2)&1);
*(video++)=c;
} |
Nous passons de 448 décalages et masques, 384 additions (1280 opérations au moins), à 128 additions, 192 masques et 320 décalages (640 opérations).
Ensuite, il faut rappeler que l'affichage n'est plus effectué directement : l'accumulation
s'effectue durant le passage de la fenêtre de calcul, pendant strip pas de temps.
La valeur maximale théorique de strip doit être de 256/7 (256 est le nombre de valeurs
possible de l'octet affiché, 7 étant le nombre maximal de particules par site). stripmax=32
a été choisi pour éviter le débordement de l'octet et conserver plusieurs entrées dans la palette pour
afficher des éléments de contrôle (boutons, curseur...). Les valeurs 0 à 223 sont réservées
à l'affichage des densités dans le tunnel, les valeurs 224 à 255 servent aux éléments graphiques
de contrôle. Ainsi, pour rendre l'affichage des densités plus cohérent, la palette peut être
changée selon la valeur de strip et conserver un contraste optimal, sans post-traitement
externe dans un autre logiciel.
L'annexe C, page 40, traite de l'accumulation lors du calcul puis de l'affichage.
Une manière plus sophistiquée pour effectuer ces opérations est d'utiliser la technique
d'explosion, découverte lors de la programmation de la routine d'affichage du curseur.
En utilisant les instruction PUNPCK d'une manière particulière, il est possible de
transformer 8 bits consécutifs en 8 octets aux valeurs choisies par des masques.
movq mm1, Sx ; S0, S1 ou S2
punpcklbw mm1,mm1
punpckldw mm1,mm1
punpckldq mm1,mm1
;ici les 8 LSB sont recopiés 8 fois. il faut donc trier ici les bits :
pand mm1,p1 ; p1 pointe vers la donnée 0x8040201008040201
pcmpeqb mm1,[=0, reg ou mem] ; mm1=0 ou 0FFh
; pour le cas de S0 : astuce ! x-(-1)=x+1
psubb mm0,mm1 ; mm0 est la valeur accumulée
; pour le cas de S1 et S2:
pand mm1,p2 ; p2 pointe vers la donnée 0x0202020202020202
; ou 0x040404040x04040404, selon S1 ou S2
paddb mm0,mm1 ; et voila ! |
Le premier problème est que les instructions PUNPCK sont pairables mais pas avec elles-mêmes,
il n'est donc pas possible d'entrelacer les 8*3 occurences de ce code, nécessaires à la fabrication
des 64 nombres de 3 bits qui seront accumulé à 64 octets. Les dépendances fortes et directes entre
les registres réduisent les opportunités de pairage et de parallélisme, empêchant le déroulement de
la boucle. Ensuite, ce code est trop lent, même s'il garde l'affichage simple : rep mosvd
suffit pour transférer les données vers la mémoire vidéo mais nous savons que cela sature le bus
externe et nous perdons des centaine de cycles CPU.
Ce code serait donc déséquilibré : il utilise trop la CPU lors du calcul et perd du temps lors de
l'affichage. Pourtant l'algorithme de strip mining permet de n'afficher qu'une fraction des données,
en fonction du paramètre strip. Il faut donc réduire au maximum le nombre d'opérations
nécessaires à l'accumulation des données, même si l'affichage est plus complexe : d'une part
le strip mining compense la perte lorsque strip est élevé, d'autre part l'entrelacement
d'instructions utiles lors du transfert permet de recueillir des statistiques permettant par exemple
d'optimiser le contraste de la palette.
L'algorithme choisi pour l'accumulation est en fait très simple et il utilise au maximum
les propriétés des données : il consiste à additionner 8*3 bits à 8 octets en parallèle, en masquant
directement, sans "éclatement" ou réorganisation, les données. Le calcul de l'accumulation prend
donc beaucoup moins de temps et la réorganisation des données est effectuée lors du transfert vers
la mémoire vidéo.
struct site {
lli a,b,c,d,e,f,g;
mur * liste;
graph *p;
lli v[8];
} *s;
lli mask=0x0101010101010101;
/* pseudo-code d'accumulation : */
for (i=0; i<8; i++)
s->v[i]+=((S0>>i)&mask)
|(((S1>>i)<<1)&mask))
|(((S2>>i)<<2)&mask)); |
Nous utilisons maintenant au maximum 8 additions, 16 OR, 24 AND et 40 décalages.
Le déroulement de la boucle offre certaines opportunités d'optimisation, en éliminant par exemple
certains décalages par des masques différents. Il suffit de décaler le
masque car (x<<1)&mask peut être remplacé par x&(mask<<1)
à certains endroits (existe-t-il beacoup de compilateurs capables de cette optimisation ?).
Ce nouveau masque ne pose aucun problème de codage mais il n'est pas possible de l'optimiser
dans la version originale de la boucle, à cause de problèmes potentiels de débordements
durant les décalages. La version finale utilise seulement 42 instructions dont 8 AND,
8 PADDB et 7 décalages. Nous sommes loin des milliers d'instructions nécessaires avec l'algorithme
original en C et nous profiterons de l'élargissement inexorable des regitres dans le futur.
Maintenant que les octets sont accumulés, il faut les afficher quand arrive la fin de la fenêtre :
le gros problème est que la fonction d'accumulation décrite précédemment mélange complétement les
octets. Nous apercevons cependant qu'ils sont ordonnés d'une manière qui ressemble à celle
de la sortie du butterfly d'un code de FFT :
v[0]: 0 8 16 24 32 40 48 56
v[1]: 1 9 17 25 33 41 49 57
v[2]: 2 10 18 26 34 42 50 58
v[3]: 3 11 19 27 35 43 51 59
ordre des octets après accumulation: v[4]: 4 12 20 28 36 44 52 60
v[5]: 5 13 21 29 37 45 53 61
v[6]: 6 14 22 30 38 46 54 62
v[7]: 7 15 23 31 39 47 55 63
Les instructions PUNPCK sont
justement prévues pour ce cas et il en faut 24 pour réorganiser tous les octets. La fonction
elle-même nécessite 58 instructions et a été chronométrée comme étant capable de saturer
le bus externe de données. Les algorithmes, les codes et toutes les explications techniques sont
fournies en Annexe C, à partir de la page 40. Les codes actuels ne permettent pas d'utiliser
les techniques d'affichage décrites ici, la technique d'"explosion" simple avec PUNPCK
(utilisée par les codes de prototypage)
subsiste . Lorsque les problèmes structurels du projet seront résolus, les codes
développés pourront être intégrés. Il est intéressant de noter que ce type de code d'accumulation
peut être utilisé pour des accumulateurs de 10, 16 ou 32 bits avec les instructions MMX normales.
D'autres tailles d'accumulateur peuvent être utilisées si l'addition sur 64 bits est disponible
mais le désenchevêtrement des données sera encore délicat.
Un code a aussi été conçu pour afficher la "densité de réorganisation" (les collisions donnant lieu
à une réorganisation des sorties), à défaut de pouvoir calculer la chiralité ponctuelle instantannée.
La sélection entre les deux versions (densité de particules ou densité de collisions réorganisées)
sera effectuée par un code automodifiant (SMC : Self-Modifying Code).
Le schéma suivant résume les algorithmes et la structure des données liées à l'affichage des densités :
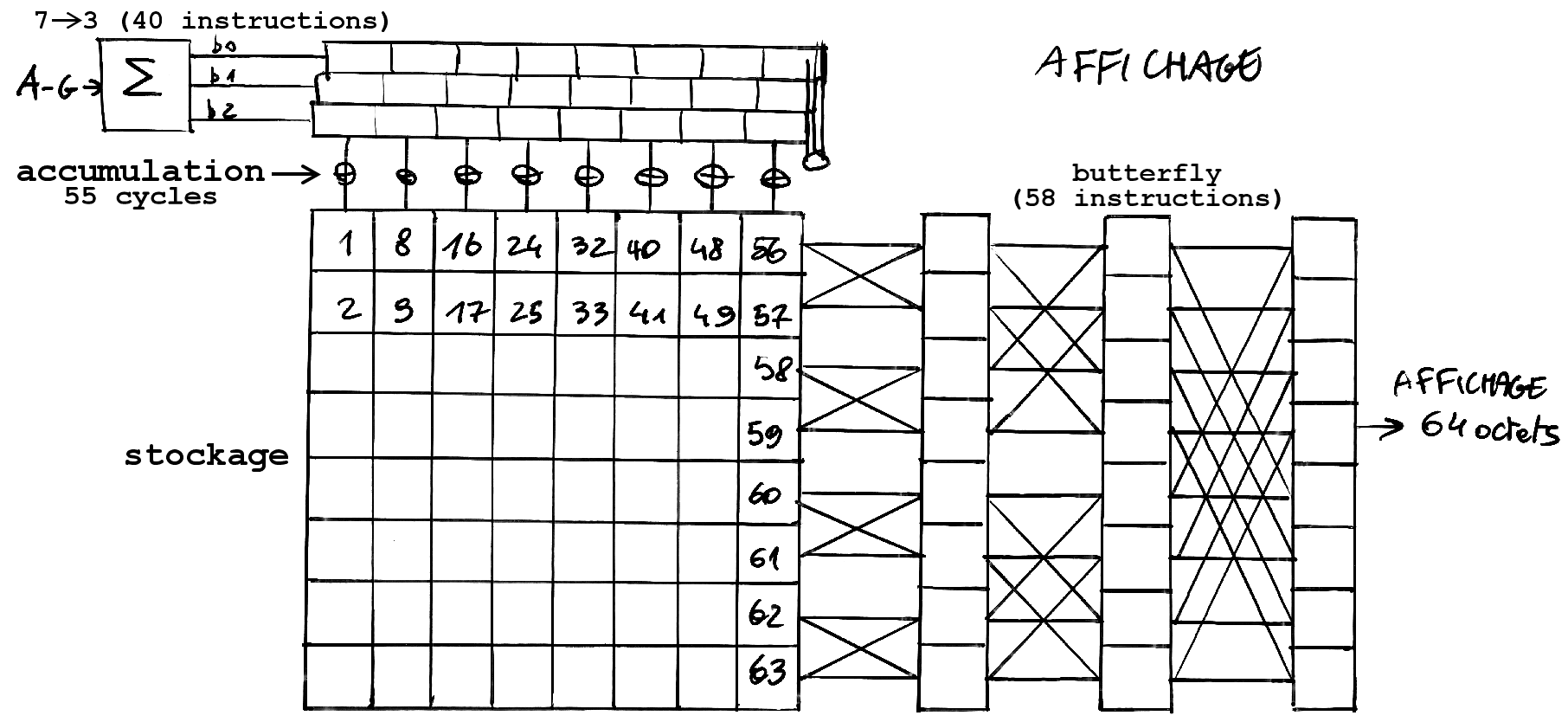
IV.7 : Analyse booléenne de l'opérateur de collision
La réalisation du projet de maitrise a souffert de plusieurs aléas dont le plus important est celui du
code de collision. Le projet avait été lancé avec la conviction que le travail serait facile grâce aux
"outils modernes" mais en réalité, seule la vieille méthode du papier et du crayon a permis d'arriver à
bout du problème.
|
La table ci-contre présente les collisions du modèle FHP-3 classique.
Il contient à la fois la valeur numérique de l'entrée et des sorties, afin de
pouvoir programmer une lookup table et les vecteurs vitesses sont
représentés pour comprendre le type de collision qui a lieu.
Ce modèle utilise un seul générateur binaire de nombres aléatoires, d'une probabilité 1/2.
Selon le bit fourni à chaque site par ce générateur, on choisit la colonne de gauche ou de droite.
La colonne de gauche est déterminée par la formule (1) et les valeurs de la colonne
de droite sont données par la formule (2).
|
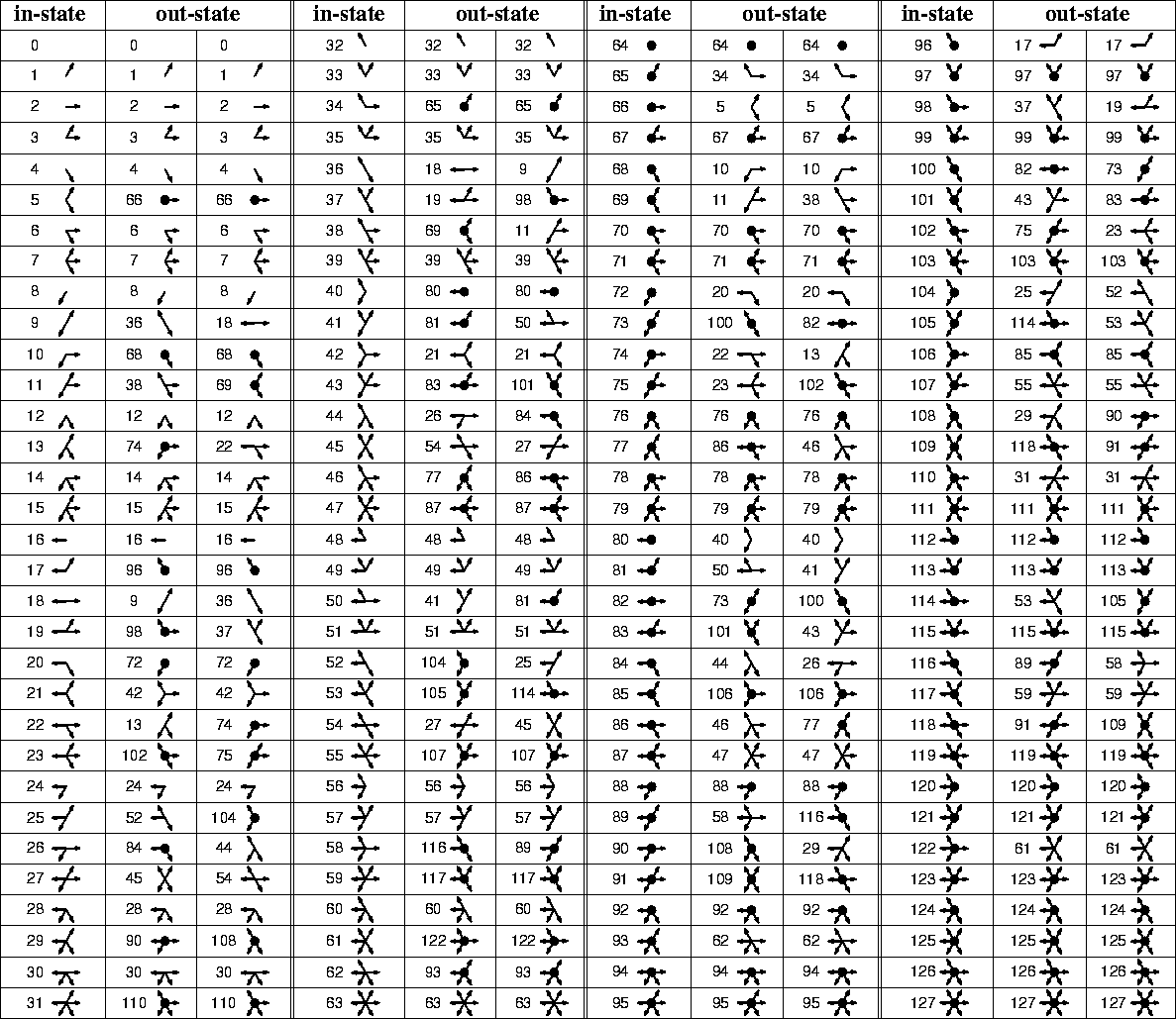
|
Les formules qui permettent de calculer les collisions sont extraites de [32]
et reproduites de la thèse de James Buick qui a aussi indiqué des corrections.
Elles sont énoncées de la manière suivante :
Soit i, compris entre 0 et 6, et 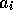 ,
un ensemble de 7 valeurs booléennes représentant l'absence ou la présence d'une particule pour chaque lien
,
un ensemble de 7 valeurs booléennes représentant l'absence ou la présence d'une particule pour chaque lien
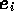 .
.
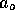 correspond à la particule immobile,
correspond à la particule immobile,
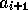 (modulo 6) correspond au lien
(modulo 6) correspond au lien 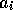 après rotation de 60°.
après rotation de 60°.
Nous pouvons alors définir les variables temporaires suivantes :
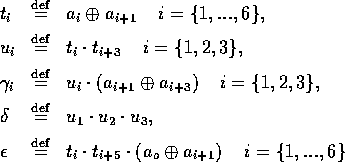
où  , a + b,
, a + b, 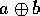 et
et 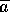 correspondent respectivement aux opérateurs booléens et, ou, ou exclusif et négation.
correspondent respectivement aux opérateurs booléens et, ou, ou exclusif et négation.
Alors 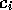 , l'ensemble des variables booléennes représentant les états de sortie, est donné par
, l'ensemble des variables booléennes représentant les états de sortie, est donné par
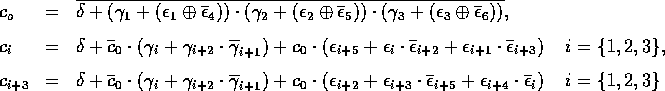 | (1) |
ou
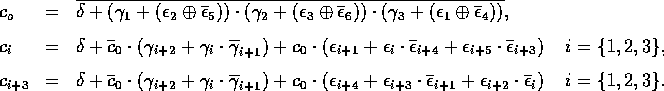 | (2) |
selon la chiralité.
Le premier problème est que je n'ai pu me procurer cette formule que récemment. Le deuxième
est qu'elle génère un grand nombre de variables temporaires qui ne peuvent toutes rentrer dans les
registres du processeur. Il faut les stocker en mémoire mais les règles de codage des x86 récents
concernant l'accès à la mémoire sont très contraignantes et rendent cette approche inefficace.
La première idée fut de partir du tableau fabriqué pour les programmes précédents. Le projet a été
basé sur l'espoir d'utiliser des outils existants pour fabriquer l'équation centrale :
- Donner le tableau à un compilateur VHDL
- Transformer la sortie du synthétiseur logique en code C
- Compiler le code C et générer du code assembleur
- Copier/coller le kernel de calcul dans le programme
- Assembler le programme
Ce détournement de l'usage d'un compilateur VHDL a été inspiré par la
pluridisciplinarité du département MIME qui dispense des enseignements
sur l'électronique et l'informatique. Tous les éléments nécessaires à
la conception de programmes assistée par ordinateur semblent réunis et fonctionner.
Cette idée espérait que les outils modernes puissent aider à automatiser la fabrication du programme
sans se soucier d'autres aspects que les collisions. Pourtant tous les niveaux sont impossibles dans
la pratique :
- Le tableau nécessite une traduction en VHDL : c'est possible mais ce n'est pas un langage de
"programmation" courant.
- Le synthétiseur est inadapté à cette tâche pour de nombreuses raisons. En premier lieu, le
type de cible a une architecture complétement différente, donc les contraintes et les règles de synthèse
ne conviennent pas. Par exemple les opérations permises par les circuits logiques programmables
ne sont pas les mêmes que celles permises par le processeur, la synthèse s'effectue par optimisation
de "sommes de produits" (un grand OU de ETs logiques). Le processeur au contraire n'a que des
instructions à deux opérandes et dispose du XOR mais pas du NOT. Il dispose de peu de registres
alors que les circuits permettent un grand parallélisme interne. En conclusion, la synthèse génère
de nombreuses opérations très parallèles (afin de réduire le chemin critique) au lieu de réduire
le nombre total d'opérations logiques à deux opérandes et de diminuer le nombre de variables temporaires.
- La transformation de rapport de synthèse en code C n'est pas une tâche aisée, elle
doit être effectuée à la main.
- Aucun compilateur à l'heure actuelle ne permet de générer de code MMX automatiquement.
- L'allocation des registres diffère entre un code généré par un compilateur et un code écrit
en assembleur.
Afin de programmer à la main le code de collisions, leur fonctionnement a été étudié plus en
profondeur. L'analyse du code VHDL fabriqué précédemment a montré que des collisions manquaient et
que les règles n'étaient donc pas saturées. La fabrication des règles de collisions a été recommencée
et a donné ce tableau suivant.
Le principe de conception repose sur le fait que les règles de collision sont plus efficaces
quand il y en a le plus possible et lorsqu'elles sollicitent au maximum la particule immobile.
Une recherche exhaustive des combinaisons et des configurations intéressantes est difficile à la main, et aucun
logiciel ne peut nous aider. Une des manières de constituer les règles est de réduire
les cas à un seul vecteur de mouvement, lorsque l'"impulsion" est dirigée dans un seul
sens. Il suffit alors de chercher les règles pour la direction puis d'appliquer cinq rotations
pour obtenir les autres. Mais ce n'est pas une règle très formelle.
A force de tâtonnements, je suis arrivé à une classification plus formelle avec un tableau
à deux dimensions, indexé par la longueur du vecteur d'impulsion et le nombre de particules
mobiles.
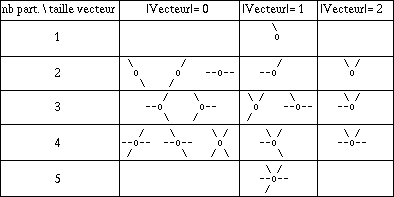 Nous remarquons que la particule immobile (G) est ignorée : elle sert à passer d'une case à l'autre
dans l'axe vertical. Ainsi, il faut une particule immobile pour passer de la configuration
1-3-1 à la configuration 1-4, alors qu'en l'absence de la particule G on sautera à la configuration 1-2.
La colonne 2 est inutilisable car le vecteur n'est pas orienté dans le
même axe d'une case à l'autre.
Nous remarquons que la particule immobile (G) est ignorée : elle sert à passer d'une case à l'autre
dans l'axe vertical. Ainsi, il faut une particule immobile pour passer de la configuration
1-3-1 à la configuration 1-4, alors qu'en l'absence de la particule G on sautera à la configuration 1-2.
La colonne 2 est inutilisable car le vecteur n'est pas orienté dans le
même axe d'une case à l'autre.
Un codage "direct" a été tenté : les équations nécessitent de nombreuses opérations, les colonnes
0 et 1 ont été laborieusement codées. Le code assembleur est très compliqué et très difficile à
comprendre. Cette approche n'est donc pas correcte. En essayant de maitriser la quantité d'opérations,
l'idée est venue de "casser" l'opérateur de collisions d'une manière différente, en utilisant
certaines propriétés de symétrie dans la différences entre l'entrée et la sortie d'un site :
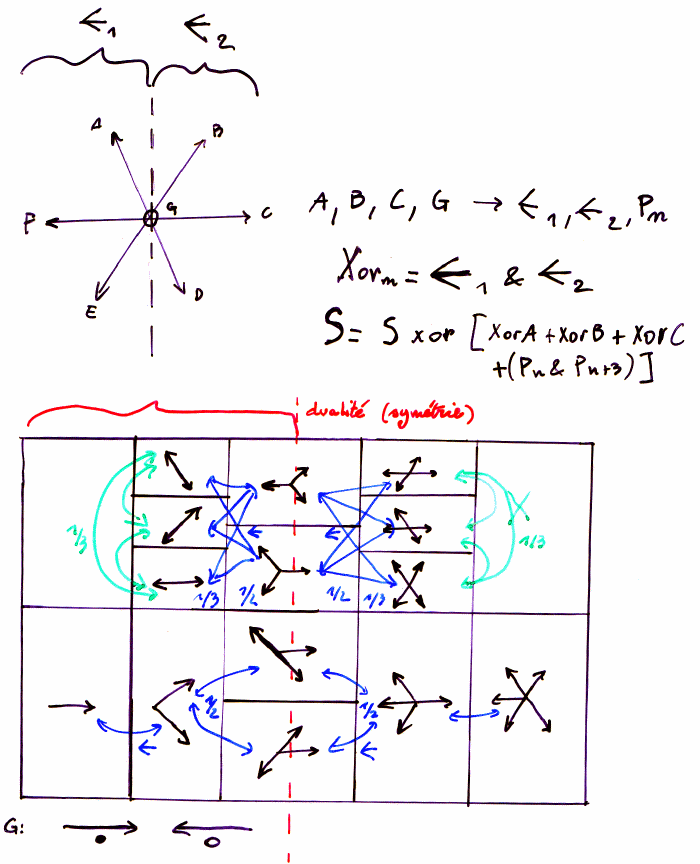 Le passage d'une case à l'autre lors d'une collision avec
réarrangement des particules est réversible et il modifie toujours la
valeur de 4 particules, de 2 manières différentes. Cette modification
peut être effectuée par un XOR et il n'y a que 3 configurations
de 4 particules à détecter : E1 (0101 ou 1010), E2 (complexe) et P (0100).
E2 est évidemment le plus difficile à mettre au point.
L'une des opérandes du XOR final sera la combinaison de ces sous-résultats.
La partie de détection est réduite à une table à 4 entrée et 3 sorties, tenant facilement
dans les registres du processeur si elle est codée explicitement. Elle
est répétée 6 fois pour toutes les combinaisons d'entrées consécutives
(ABCG,BCDG,CDEG,DEFG,EFAG,FABG).
Le passage d'une case à l'autre lors d'une collision avec
réarrangement des particules est réversible et il modifie toujours la
valeur de 4 particules, de 2 manières différentes. Cette modification
peut être effectuée par un XOR et il n'y a que 3 configurations
de 4 particules à détecter : E1 (0101 ou 1010), E2 (complexe) et P (0100).
E2 est évidemment le plus difficile à mettre au point.
L'une des opérandes du XOR final sera la combinaison de ces sous-résultats.
La partie de détection est réduite à une table à 4 entrée et 3 sorties, tenant facilement
dans les registres du processeur si elle est codée explicitement. Elle
est répétée 6 fois pour toutes les combinaisons d'entrées consécutives
(ABCG,BCDG,CDEG,DEFG,EFAG,FABG).
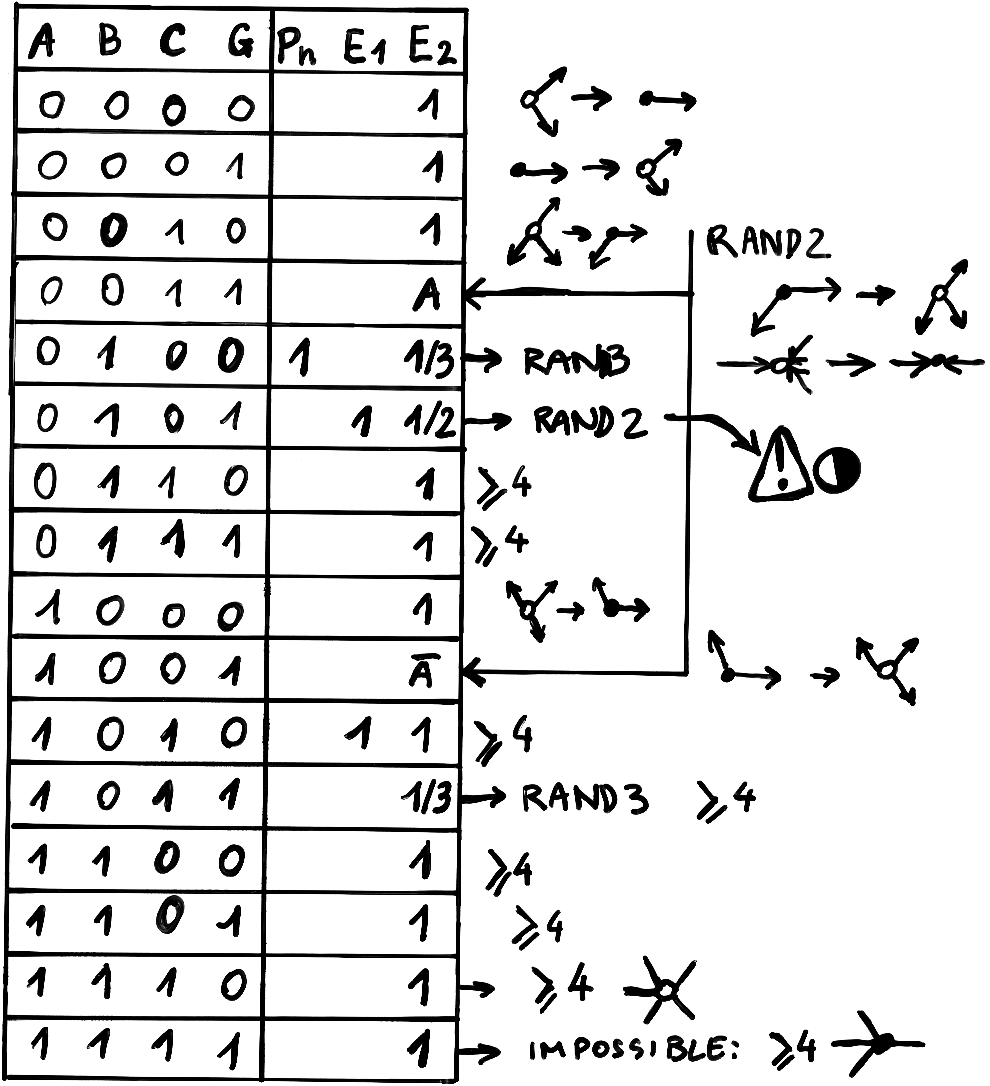
|
Cette table fait appel à plusieurs astuces de simplification, dont :
* La dualité particule/trou qui permet de ne traiter que la moitié des cas.
Ainsi, lorsqu'il y a plus de 3 particules en entrée, les particules A à F sont inversées,
ce qui ne change pas la différence à appliquer en sortie. Cette détection du nombre de particules
fait l'objet d'un code préliminaire avant l'application de la table.
* La particule G sert pour affiner la sélection du type de collision : E1 et E2 sont
complétement indépendants.
La difficulté conceptuelle réside dans l'utilisation correcte des valeurs aléatoires.
En sortie de ce tableau, nous disposons de plusieurs sous-résultats
dont la combinaison permet d'effectuer un XOR sur les particules du site traité.
|
IV.8 Méthodes de programmation manuelle en assembleur
Ce chapitre présente la technique d'optimisation en assembleur qui a été utilisée dans certaines
zones du programme expérimental. Malheureusement, certaines parties sont tellement complexes que
les bugs y sont inextricables, le programme en annexe A présente
la version fonctionnelle mais pas complètement optimisée. Tous les détails importants sont consignés en
annexe C.
La technique présentée ici est l'évolution naturelle des techniques manuelles de codage pour Pentium,
ou en général pour processeur pipeliné superscalaire. Elle n'est pas dérivée de techniques du "Dragon
Book" [6] qui traite trop peu de l'optimisation et sous l'angle de code
généré par compilateur, donc des techniques de base et évidentes pour un humain. Le Dragon
Book ne traite pas non plus des processeurs superscalaires et suppose un nombre "suffisant"
de registres. Nous nous trouvons dans un cas où la technique de "coloration de registres" à la main
n'est pas possible à cause de la taille des graphes à traiter et du faible nombre
de registres disponibles. Nous allons voir ici les contraintes cruciales qui ont nécessité
de concevoir cette technique manuelle.
La plateforme cible de nos efforts est le Pentium MMX et le Pentium II, deux processeurs au nom
similaire mais aux caractéristiques fondamentalement différentes. Le premier est un processeur
superscalaire à deux pipelines de cinq à sept niveaux, alors que le PII est une machine complexe
qui exécute les instructions dans le désordre afin de pallier les lenteurs de la mémoire.
Il n'est pas possible de faire deux versions du code pour des raisons de vitesse de codage.
D'ici à ce que le projet aboutisse vraiment, le Willamette sera répandu. Nous allons nous efforcer
de retenir les caractéristiques de codage communes pour les deux plateformes, ce qui permet au
code de fonctionner "honnorablement" partout au lieu d'être trop ciblé. En effet, le code n'a pas
été testé sur des processeurs concurrents, bien que Yannick Sustrac ait reporté
des performances intéressantes avec son Cyrix.
La raison principale et cruciale d'utiliser l'assembleur dans ce projet est que les compilateurs actuels
ne peuvent pas générer "automatiquement" les instructions MMX. Au mieux, ils supportent des pragmas, des
librairies ou l'inclusion d'opcodes, mais alors quel est l'intérêt du compilateur s'il faut faire
soi-même le codage en assembleur ?
Il est très peu probable que l'extension MMX du jeu d'instructions x86 ait été destinée à être
facilement utilisée dans les compilateurs classiques. Par contre, comme nous pourrons le voir plus tard,
Intel a compris l'intérêt d'un jeu d'instructions simplifié et plus orthogonal. Même si les caractéristiques
sont encore éloignées d'un jeu d'instruction RISC habituel, l'othogonalité du codage MMX facilite beaucoup la programmation : pas de registre spécial ni d'opcode complexe.
| Intel Architecture MMX(TM)
Instruction Set (Courtesy of Intel) |
| Packed Arithmetic | Wrap Around | Signed Sat | Unsigned Sat |
| Addition | PADD | PADDS | PADDUS |
| Subtraction | PSUB | PSUBS | PSUBUS |
| Multiplication | PMULL/H |
| Multiply & add | PMADD |
| Shift right Arithmetic | PSRA |
| Compare | PCMPcc |
| Conversions | Regular | Signed Sat | Unsigned Sat |
| Pack | | PACKSS | PACKUS |
| Unpack | PUNPCKL/H |
| Logical Operations | Packed | Full 64-bit | |
| And | | PAND |
| And not | | PANDN |
| Or | | POR |
| Exclusive or | | PXOR |
| Shift left | PSLL | PSLL |
| Shift right | PSRL | PSRL |
| Transfers and Memory Operations | 32-bit | 64-bit |
| Register-register move | MOVD | MOVQ |
| Load from memory | MOVD | MOVQ |
| Store to memory | MOVD | MOVQ |
| Miscellaneous |
| Empty multimedia state | EMMS |
|
Nous voyons dans le tableau ci-contre un extrait de la présentation de l'extension MMX par Intel,
avec la base des mnémoniques (sans leurs nombreuses variations).
Le jeu d'instruction MMX est à la fois plus organisé que les instructions
normales et pourtant il n'est pas complétement orthogonal. Nous regrétons par exemple
que certains formats ne soient pas supportés avec certaines instructions, que certaines
instructions comme la rotation ne soient pas inclues, que seules 4 opérations logiques soient
disponibles (la négation d'une donnée nécessite 2 instructions !) et
d'autres détails qui se révèlent dans la pratique. A un niveau supérieur, les
instructions sont toujours au format op reg,reg/mem ce qui limite les
possibilités, surtout avec seulement 8 registres. Enfin, selon les architectures, les limitations
sont variées et parfois contradictoires. Il faut pouvoir jongler entre les nombreuses
contraintes et éviter tous les types de blocages, au niveau du décodage, de la mémoire et
des unités d'exécution, tout en allouant correctement le peu de registres disponibles.
|
Les plus grandes limitations concernent les règles de décodage et de pairage : certaines instructions
ne peuvent être décodées qu'à certaines positions du 'slots' de pairage. Pour le PMMX, les instructions vont par
paire (une par pipeline, U et V), alors que sur le PII le décodage doit suivre la règle 4-1-1 :
le groupe doit faire moins de 16 octets, la première instruction du groupe ne peut générer
que 4 µops et les deux suivantes qu'une seule (les tables de correspondances instruction->µops sont
données par les manuels Intel). Les règles sont gênantes dans la pratique et nous retiendrons
principalement celles-ci :
- Pairage de style PMMX : deux instructions par cycle.
- Instruction d'écriture ou de lecture mémoire dans le premier 'slot' (pairage en U).
- Instructions de Shift dans le pipeline V.
- Ecriture vers la mémoire : deux cycles après la modification du
registre (contrainte du PMMX).
Les manuels de Intel contiennent de très nombreuses remarques sur tous
les aspects de la programmation, tout en restant très évasifs sur les
contraintes pratiques. Il faut pouvoir jongler avec le faible nombre
de registres et les instructions bancales, les formats dissymétriques
et les slots des instructions. Cela reste possible à faire à la main
pour dix ou vingt instructions mais ne convient pas pour le type de
code nécessaire pour le projet : il faut optimiser plus de 500 instructions
dans le coeur de la boucle.
J'ai donc développé, en programmant à la main des exemples de plus en
plus complexes, une technique basée sur les graphes de dépendances de données.
L'astuce principale réside dans l'algorithme très simple pour générer
le code optimisé (en lisant le graphe séquentiellement par la fin) mais cette facilité
est largement compensée par le travail nécessaire pour préparer le graphe.
Le workflow de programmation est le suivant :
- Vérification de l'algorithme par du pseudo-code dans un langage
de haut niveau, par exemple avec Turbo Pascal
- Fabrication du graphe de dataflow (voir le
graphe initial)
- Réduction de la largeur du graphe si nécessaire, détermination des variables à stocker
temporairement en mémoire
- Détermination des "faisceaux" (critère du plus petit, sauf avec ANDN)
- Détermination du "chemin critique" (CDP en anglais)du graphe
- Réarrangement autour du CDP
- Contrainte principale : équilibrage des load/store
- Association des registres aux faisceaux
- Détermination des "slots" de décodage
- Arrangement fin des instructions
- "Lecture" du graphe (par un simple balayage) et écriture du code
assembleur correspondant
Bien sûr, selon la complexité des opérations, il faudra plus ou moins de travail
sur le graphe pour équilibrer toutes les branches. Le workflow n'est pas rigide et certaines parties
peuvent être sautées ou inversées. Il faut aussi souvent reprendre
le travail à partir d'une étape précédente pour éviter des cycles morts causés par
un registre manquant ou un accès mémoire mal placé, ce qui n'apparait
pas immédiatement lors des phases initiales. Il faut donc avoir toutes
les étapes en tête afin d'appliquer la bonne optimisation au bon moment.
Chaque étape nécessite à la fois un algorithme et du bon sens. Il ne
s'agit pas d'appliquer aveuglément une méthode mais d'étudier au cas
par cas l'influence de telle ou telle transformation. L'analyse du
chemin critique du graphe peut ne pas être nécessaire si le graphe est
simple et petit, toutefois elle devient nécessaire pour casser
certaines dépendances complexes. L'allocation des registres se fait en
deux étapes : les branches du graphes sont d'abord réunies en "faisceaux"
lorsqu'il faut déterminer quel registre sert de destination (le choix
n'est pas possible pour l'instruction PANDN par exemple), puis les
registres sont associés aux faisceaux au dernier moment, lorsque le
graphe est équilibré. Ce dernier est toujours balayé par le fin :
on remonte et on alloue les registres en commençant par le premier
registre libre. Un registre est donc "occupé" lorsqu'il est associé à
un faisceau et il est libéré lorsque le faisceau se termine : le
registre est donc libre de servir pour un autre faisceau.
Cet algorithme est presque automatique lorsque le graphe est adapté
au nombre exact de registres disponibles, c'est la raison pour laquelle
la préparation est si importante.
Par exemple, la table de détection des collisions est représentée
dans le graphe ci-contre, après traduction du pseudo-code et
explicitation temporelle des dépendances. A ce stade d'étude, le but est d'explorer
au maximum le parallélisme des instructions permis par le graphe.
Cela permet de dégager les axes importants et le chemin critique, les
besoins en instructions d'accès à la mémoire, leur répartition...
| 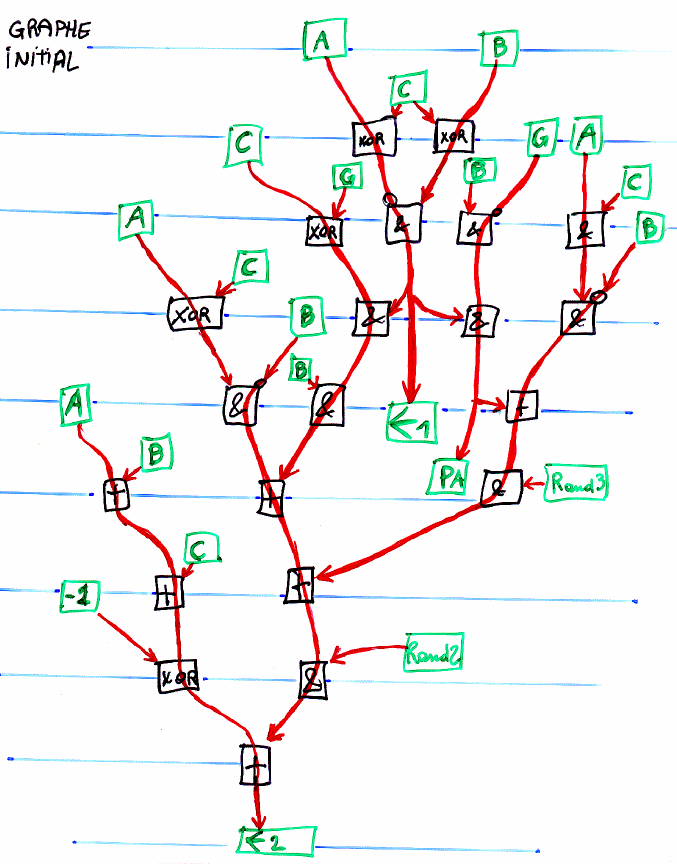 |
|
Ensuite, le nombre de registres est réduit afin de préserver 3 registres tournants
(pour le renommage des entrées). La répartition des accès à la mémoire
devient importante. Les feuilles sont repliées, les données
persistantes (celles qui resteront dans les registres) sont choisies
en fonction du nombre d'utilisation, les autres sont stockées en mémoire.
Une fois les registres alloués et le graphe prêt, on va balayer
le graphe de bas en haut et de gauche à droite, tout en consignant les
noeuds rencontrés sous forme d'opcodes dans le fichier assembleur.
Lors de cette phase terminale, il faut veiller à ce que les règles de
pairage soient respectées. Si une des instructions précédemment
consignées entre en conflit (slot ou dépendance de registre par
exemple) avec l'instruction courante, il faut réorganiser le balayage
de la ligne et cela déborde parfois sur d'autres lignes.
|
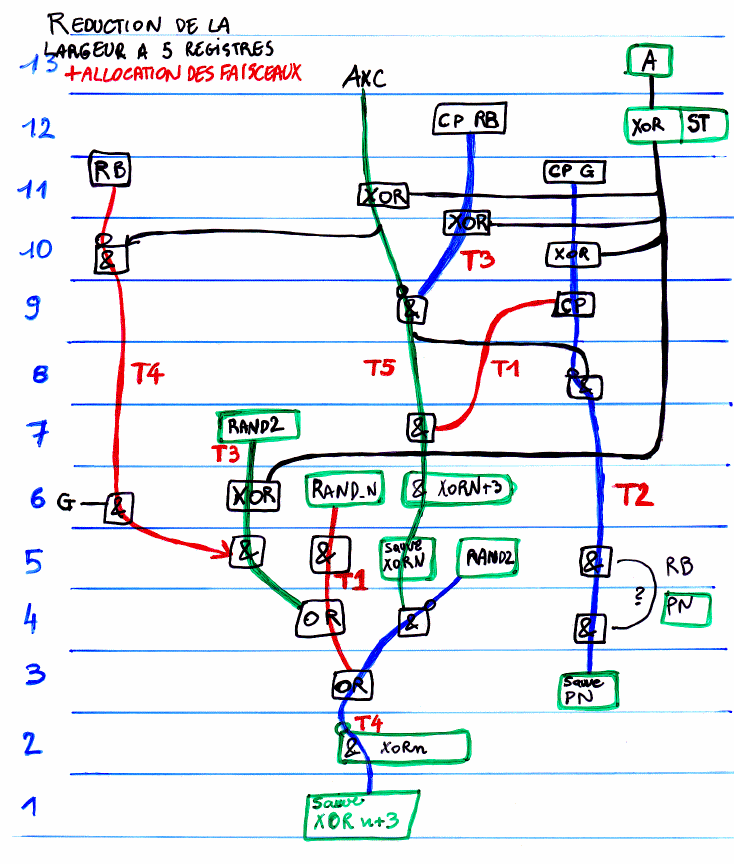 |
Le code de collision est décrit schématiquement ci-dessous, comme s'il
devait être câblé :
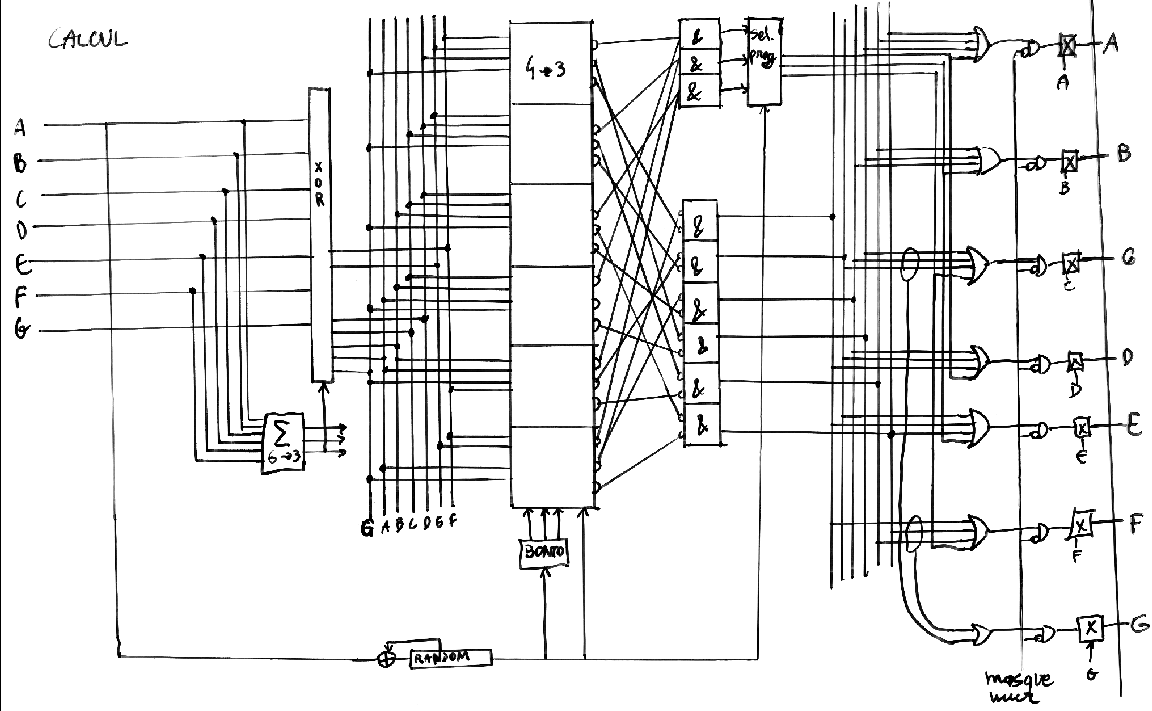
- La première partie compte le nombre de bits afin de profiter de la
dualité du modèle et ainsi réduire la complexité de la table. Si le
nombre de bits à 1 dans les particules A à F est supérieur à 3, toutes
les particules sont inversées. Cela revient à effectuer un XOR de ces
particules avec le bit 2 du résultat.
- La deuxième partie est la détection elle-même : elle prend
4 entrées et génère 3 résultats temporaires en fonction du tableau et
du code décrits précédemment. Les registres sont alloués afin de
pouvoir garder au moins trois valeurs d'entrée et les faire "tourner"
sans nécessiter d'accès mémoire.
- La troisième partie combine les résultats temporaires. Une
partie de ces opérations (combinaison des Pn) est effectuée dans la deuxième moitié de la
détection pour bénéficier de la localité des données. L'autre partie
de la combinaison est entrelacée avec le code de déplacement de
données qui utilise aussi une allocation "tournante" des registres.
La structure des données dans le tableau est représentée ici :
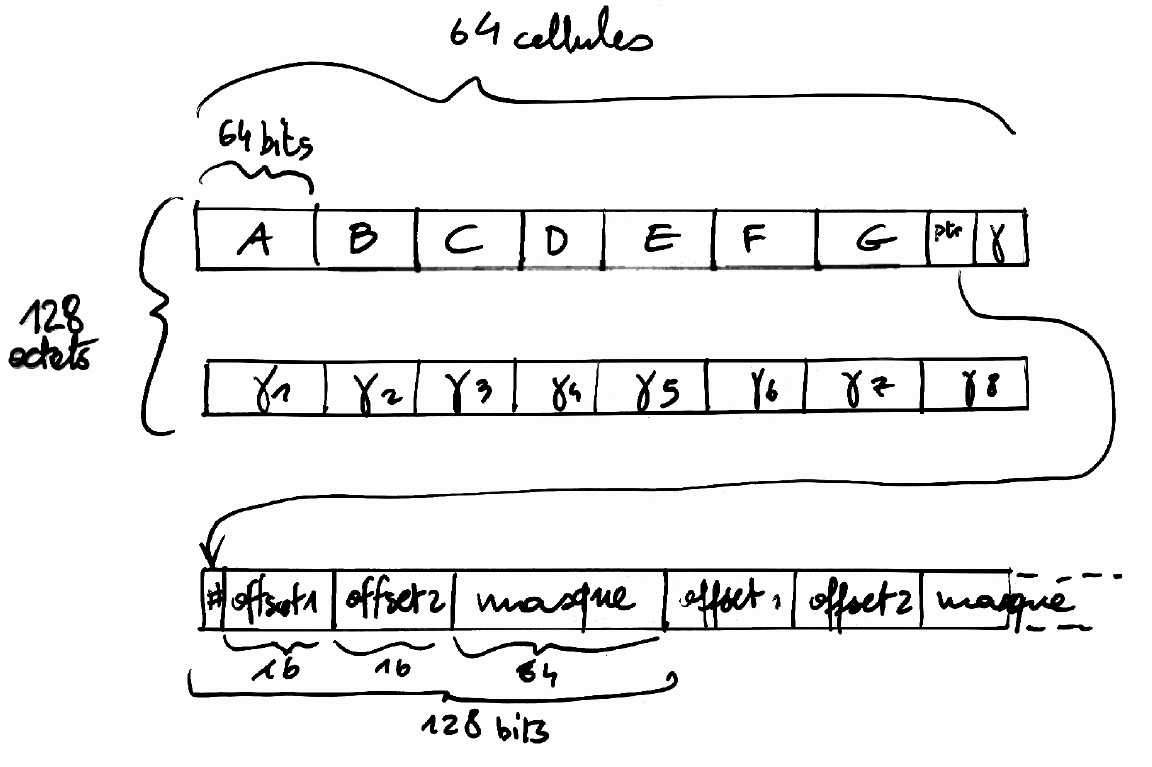 Il n'existe pas de debugger sous GPL, compatible avec NASM, en mode protégé/CPL0.
Le développement se fait donc à l'aveuglette et le bon sens est mis à rude épreuve, en raison du
nombre important et croissant d'éléments à prendre en compte.
Il n'existe pas de debugger sous GPL, compatible avec NASM, en mode protégé/CPL0.
Le développement se fait donc à l'aveuglette et le bon sens est mis à rude épreuve, en raison du
nombre important et croissant d'éléments à prendre en compte.
Le développement d'un code sain aussi complexe nécessite de bonnes habitudes
de codage et beaucoup de bon sens. Par exemple, lorsqu'un morceau de code fonctionne, il n'y a plus
besoin dans la plupart des cas de le modifier : il ne faut pas attendre qu'un bug apparaisse pour
sauver le fichier sous un autre nom. Lorsqu'un problème se déclenche, cela limite le nombre de lignes
à vérifier et permet de toujours avoir un programme fonctionnel sur lequel se rabattre
lorsque le développement est dans une impasse. Ainsi le loader 32 bits est stable
car il est développé depuis longtemps, il remplit son rôle et la plateforme ne change pas.
Les bugs ne sont pas des êtres malins destinés à nous faire perdre la raison mais c'est un écart du programme
dans la réalisation de la fonction désirée. Puisqu'un ordinateur effectue exactement ce qu'on lui demande,
l'écart ne peut provenir que des ordres erronés que le programmeur lui fournit.
Les bugs d'inattention constituent environ la moitié du temps passé à débugger, même s'ils sont souvent
plus faciles à détecter par une relecture attentive. Ils se situent surtout dans l'écriture du programme :
label déclaré mais pas utilisé, erreur de syntaxe, erreur d'adresse, mauvaise taille d'un mot...
Les erreurs d'ignorance sont plutôt liées aux aspects techniques qui sont plus complexes avec des
multiprocesseurs modernes. Un problème peut survenir quand on croit que l'ordinateur effectue certaines
opérations automatiquement (maintenir la cohérence des mémoires) ou différemment (ordre d'écriture des mots)
imprévisibles avec un processeur exécutant les instructions dans le désordre. La relecture attentive des manuels
permet souvent de lever certaines ambigüités ou a prioris
Pour chasser les bugs, les mêmes recettes sont applicables pour toutes les situations :
1) Relire très attentivement le code, plusieurs fois si nécessaire. Simuler mentalement le fonctionnement
du processeur et l'état de chaque registre, comparer avec les symptômes et chercher des similitudes avec ceux-ci.
2) Réunir tous les indices, tous les symptômes et noter toutes les conditions d'utilisation
lorsque le bug se déclare. Cela peut aider à déterminer la partie fautive. Par exemple, si le bug est un problème
d'affichage, il faut déterminer toutes les parties du code qui accèdent à l'écran, directement ou non.
3) Isoler la partie fautive : la technique la plus simple est de mettre en commentaire (ou %ifdef zorglub)
certaines parties du code récemment modifiées puis restreindre progressivement les recherches par dichotomie
jusqu'à ce que le bug soit circonscrit. Cela peut prendre une minute ou plusieurs heures et il ne faut pas hésiter
à remettre en cause toute la structure du programme.
4) Identifier la dépendance entre les données et les codes concernés : on découvre parfois que l'erreur
vient d'une autre partie que la partie incriminée ou détectée par la dichotomie. Le bug découvert peut être
la conséquence d'une erreur en amont mais qui ne se manifeste que dans certaines conditions que la partie
incriminée remplit. Certaines données ou certaines parties du code peuvent déclencher un comportement indésiré
ou inattendu. Le plus souvent, il s'agit "simplement" d'un oubli ou d'une erreur de frappe. Par exemple,
mettre une relocation d'adresse vers l'écran au lieu du tunnel. Dans l'empressement, ce type d'erreur est facile
à commettre mais aussi à corriger. Il en va différemment du renommage des registres ...
5) Si trop de temps s'est écoulé lors du débuggage, il faut souvent tout recoder à partir de zéro.
Il est parfois dix fois plus rapide de recommencer que de tout analyser. Le nouveau code est même
souvent de meilleure qualité car les bugs se cachent souvent dans les parties récentes et peu éprouvées,
qui auront été mûries depuis le premier jet. C'est parfois la solution de la dernière chance pour éliminer
les bugs les plus récalcitrants.
Il n'est pas forcément nécessaire dans ce cas de disposer d'un débogueur interactif avec suivi du code source :
il faut de la méthode, respecter quelques règles simples et surtout
ne jamais faire confiance aveuglément à un code sans l'avoir testé dans les conditions d'utilisation prévues ...
IV.9 : Réalisation et résultats :
Le code utilisé actuellement n'est pas la version définitive du programme : le léger bug dans les
collisions passe presque inaperçu mais empêche d'avoir un résutltat réellement utilisable. La version
beta est toutefois suffisamment rapide pour montrer le gain substantiel apporté par l'analyse soignée
du programme. Sa vitesse d'exécution a été comparée sur le même ordinateur avec un autre code en C
d'allure plus classique :
plateforme : Pentium MMX 200MHz, SDRAM 66MHz, L2 : 256Ko
géométrie : 1000 itérations sur 1024*640 (655M site calculés)
SP65.asm: 15 secondes, strip=6, zoom=4:1
vitesse : environ 43Mc/s
Programme de Benjamin Temko (voir l'annexe D)
compilation:
gcc -I/usr/X11R6/include -lX11 -L/usr/X11R6/lib -O3 fhp_0.c
run :
nice --20 time -o perf ./a.out
58.76 user
0.44 system
1:00.87 elapsed
97% CPU
(0 avgtext+0avgdata 0maxresident) k0 inputs+0outputs
(153major+178minor)page faults
0 swaps
vitesse : 11.2Mc/s
Le programme en version beta est quatre fois plus rapide qu'un bon code compilé.
Cette différence devrait varier selon la plateforme, la version du compilateur ou la version
du code. Il faut remarquer cependant que le gain majeur se trouve dans l'utilisation
de larges données (64 bits au lieu de 32) et de l'algorithme de strip mining qui garde
plus longtemps les données en mémoire cache, ce qui suffit à donner l'avantage avec le Pentium MMX.
Le Pentium II décode plus d'instructions par cycle et sa cache est plus puissante, mais il est
peu probable que GCC sache utiliser tous ces derniers raffinements technologiques : il n'est pas
dans les attribution d'un compilateur de changer la taille des données ou de modifier l'algorithme
de balayage (s'il devait exister un compilateur assez sophistiqué pour appliquer automatiquement
le strip mining à un problème aussi complexe que le calcul FHP).
La version alpha du code de collision (lorsqu'il sera débogué) devrait permettre d'améliorer la vitesse
d'environ 20 ou 30% grâce à un meilleur scheduling des
instructions dans la phase de détection et de déplacement. La meilleure performance
absolue actuelle a été mesurée au MIT en janvier 2000 sur un Pentium III à 550MHz :
taille: 860*736, cycles par pas de temps : 2,3M, 3,6 cycles par site, soit 150 Mc/s.
Bien que la calibration ait été effectuée, toutes les conditions n'ont pas pu être réunies pour
améliorer la performance (je n'avais pas pu emporter toutes mes disquettes). Dans l'absolu, il est
probable qu'on puisse calculer sur cette plateforme jusqu'à 400Mc/s en utilisant l'extension SSE
(mots de 128 bits) et peut-être 800Mc/s en bi-processeur. Toutefois, à cette vitesse, le problème sera la
communication et la synchronisation (MESI=lent) entre les processeurs.
L'expérience suivante a été réalisée pour fabriquer une petite animation illustrant les capacités du programme
existant. Le temps de calcul total est de quelques minutes, en comptant le long temps de sauvegarde des images
qui ont été choisies pour leur esthétique, non pour leur intérêt scientifique. Le nombre de pas entre
les images n'est pas fixe mais permet de montrer l'intérêt d'un affichage plus évolué, non en "noir ou blanc".
Les dimensions des images suivantes tiennent compte de la projection sur le réseau hexagonal (sin(60°)).



Ecoulement après 528 pas de temps :
la deuxième chambre se remplit lentement
et les artefacts hexagonaux sont visibles.
T = 4501 : le flux commence
à se distordre.
T = 6010



T = 6316
T = 6931 : le flux est moins marqué,
noyé dans le bruit.
T = 8089 : la pression et la vitesse sont
favorables
pour faire disparaitre les
artefacts hexagonaux mais
le contraste est
trop faible pour distinguer les écoulements.
| | | | | | | | | | | |
Nous voyons ici les limites de l'affichage de la version de développement : le bruit rend
la distinction de phénomènes fins difficile. La refonte du programme permettra d'inclure le
code d'affichage à niveaux de gris qui est décrit en au chapitre IV.6.
L'expérience s'est déroulée sur le PII-350 du département MIME. Elle consiste en la diffusion d'une masse de particule
de la chambre gauche à la chambre droite du tunnel. Les chambres étant séparées par une paroi munie d'un "trou" de
quelques pixels, légèrement décentré pour que le flux de particules oscille. Après quelques dizaines de milliers
de pas de temps, la densité dans les deux chambres est similaires et le flux disparait, laissant une "bouillie
brownienne homogène" à l'écran. Les dimensions et les paramètres initiaux sont les suivants :
- chambre gauche : densité : 1, hauteur : 725, largeur : 434
- chambre droite : densité : 0, hauteur : 725, largeur : 267
- paroi : largeur du trou : 26 noeuds
- vitesse : strip=32, 2014269 cycles CPU par pas de temps, 5,75 ms pour balayer un tableau de
704*728=512512 noeuds, soit 89 millions de noeuds par seconde.
L'image suivante montre le résultat de la routine de calibration du strip mining. Nous pouvons y apercevoir
les caractéristiques de la mémoire et en particulier mesurer le speedup permis par l'algorithme,
par rapport à un balayage linéaire normal (4981/2014=2,47). En particulier, le speedup varie peu
au-delà d'un strip mining de 10 lignes, la décroissance est dûe à la réduction de la bande passante utilisée
par l'affichage et est en 1/x.

Partie V : Plateformes dédiées
V.1 : Introduction :
Les algorithmes de gaz sur réseaux ont déjà fonctionné sur une large variété de machines dans le monde,
par exemple : Alpha, Apple, CRAY-XMP, CRAY-2, Connexion Machine 200, Connexion Machine 5,
FPS 164, IBM RS6000, IBM 3090, PC (Intel et clones), SUN/SPARC (jusqu'à 256 CPU), Silicon
Graphics Origin 8-CPU, VAX...
La nature du modèle des gaz sur réseaux s'adapte à une très grande variété de machines,
des processeurs 16 bits aux calculateurs vectoriels parallèles en passant par les machines de bureau
actuelles. Elle permet aussi aux électroniciens de créer des machines dédiées, plus ou moins
configurables : c'est le sujet de ce chapitre.
Les avantages sont nombreux : si une programmation très soignée permet de "gagner" 3 ans en performance,
elle peut en faire gagner le double ou plus dans certains cas. Par exemple, dès ses débuts,
la CAM-8 a atteint des performances encore inégalées par les stations de travail actuelles.
Le parallélisme inhérent au modèle permet aussi de créer des architectures modulaires qui peuvent s'adapter
aux contraintes budgétaires fluctuantes, laissant espérer des montées en puissance vertigineuses.
Cela permet enfin de résoudre le plus simplement du monde des problèmes de plus en plus difficiles
sur les plateformes actuelles : un simple fil peut remplacer de nombreuses lignes de code.
Tous les essais effectués ces quinze dernières années ont aussi montré les nouveaux problèmes qu'une
architecture dédiée entraine. Tout d'abord, le manque de débouchés sur le marché du grand public marginalise
les efforts : combien de personnes veulent calculer un milliard de sites FHP par seconde ?
La conséquence directe est que ces architectures suscitent peu d'intérêt réel en dehors du monde
restreint des gaz sur réseaux, donc les machines existantes ne sont que des prototypes.
Les autres machines sont restées dans l'imagination des rêveurs : si concevoir une architecture
"accueillante" pour les gaz sur réseaux semble très facile, les problèmes électroniques et de moyens
matériels sont bien différents dans la réalité pour un projet de cette échelle.
Enfin, il ne faut pas perdre de vue qu'une fois construit, le matériel n'évolue pas. Il faut souvent
revoir complétement l'architecture pour chaque génération de machine, comme pour un ordinateur
normal, mais le coût de développement est lourd et constant, à la charge du laboratoire qui lance le projet.
Il n'y a donc pas de "lignée" de calculateurs dédiés comme il y en a pour les voitures, les
logiciels, les avions ou les ordinateurs. Les changements d'organisation dans les entrailles de la machine
entre chaque nouveau prototype obligent à réécrire tout le logiciel de gestion
pour chaque version. Les cycles de développement sont donc très longs et on perd une partie de l'avance
par rapport à des logiciels sur des stations de travail.
Les quatre premiers chapitres décrivent des implémentations réelles, les suivants sont des études de
cas imaginaires (architecture fiction).
V.2 : RAP-1 :
Mis au point vers 1986 par Dominique d'Humières et André Clouqueur à l'Ecole Normale de la rue d'Ulm,
c'est une machine typique de son temps comme le montrent ses caractéristiques.
Ses performances sont de 6,5Mc/s, ou 256 sites par 512 à 50 Hz. Les sites peuvent contenir
16 bits qui sont mis à jour linéairement par une LUT (2 SRAM de 64Ko)
et l'étude en cours peut être visualisée sur un écran VGA
indépendant (synchronisation directe, pas de frame buffer). L'hôte est un
PC et les informations peuvent être post-traitées
par un VAX en local [11].
Le RAP-1 a une structure proche de la CAM-6 mais ces deux architectures resten distinctes.
La mémoire centrale du RAP-1 est composée de VRAM, des puces DRAM de 64 Kbits conçues pour les cartes
vidéo pouvant lire et écrire une donnée en un cycle grâce à deux ports séparés. Des circuits
spéciaux d'adressage permettent la réécriture vers les sites voisins pour certaines lignes,
ce qui permet de gérer les voisinages hexagonaux, de Moore ou de Von Neumann. La CAM-8 permet
la réécriture du résultat de chaque site vers n'importe quel autre site.
Le "RAP-1" signifie "Réseau d'Automates Programmable" et n'a plus qu'un intérêt historique
actuellement. Il est limité architecturalement et ne permet pas de contrôle fin ou d'actions
complexes comme le permettent les logiciels. La performance, qui nous intéresse ici, est largement
dépassée par les PC actuels.
Voir l'article dans [20] pour plus de précisions architecturales.
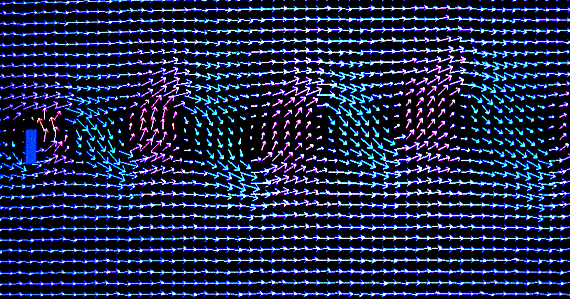
Une allée de Von Karman calculée sur RAP-1 et post-traitée.
V.3 : CAM-8 :
La CAM-8 est probablement la machine la plus intéressante actuellement. Elle est issue des recherches de
Tomaso Toffoli et Norman Margolus au MIT où ils ont conçu plusieurs générations de "CAM" (Cellular
Automaton Machine). Ils ont donc une expérience et une renommée qui leur ont permis de concevoir
une architecture flexible et performante. En particulier, sa flexibilité est bien supérieure
par rapport au RAP-1 (dont elle s'inspire un peu), ce qui lui vaut d'être encore en usage.
Dix à quinze exemplaires ont été fabriqués depuis 1992 : un record pour le domaine !

Une boite CAM-8 avec une carte insérée sur laquelle on aperçoit certains ASIC.
| |
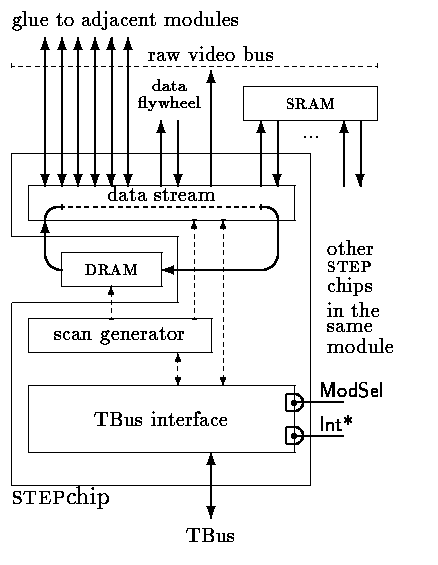
Description d'un ASIC (STEPchip)
(extrait du manuel de la CAM-8).
|
La CAM-8 est une machine complexe, décrite dans le manuel disponible sur le site qui lui est dédié
(http://www-im.lcs.mit.edu/cam8/ps/hard_ref.ps).
Pour résumer, la machine est conçue sur plusieurs échelles : système, boîte, carte et ASIC.
Le système consiste en une ou plusieurs boites reliées entre elles dans un réseau torique 3D,
ce qui permet d'en connecter en très grand nombre en parallèle sans que surgissent des problèmes
architecturaux ou logiciels.
Une boite contient 8 cartes reliées par un fond de panier. Le fond de panier n'est pas un bus
mais une zone de câblage permettant de réaliser des topologies plus ou moins complexes. C'est la seule
partie qui requiert une intervention physique. La mémoire contenue dans une boîte
est équivalente à 16 mégaoctets.
Chaque carte contient des puces mémoire (DRAM) et 16 circuits intégrés spécialisés (ASIC) qui
effectuent les "opérations" de la machine. La fréquence d'horloge est de 25 MHz et les cellules
sont traités sur la carte avec une largeur de 16 bits par une LUT.
Les ASIC concentrent toute l'intelligence de l'architecture. L'utilisateur peut contrôler
de nombreux paramètres comme la largeur des cellules, le nombre de dimensions ou les conditions
aux limites (bouclage ou chambre close). Leur configuration nécessite de nombreux efforts logiciels.
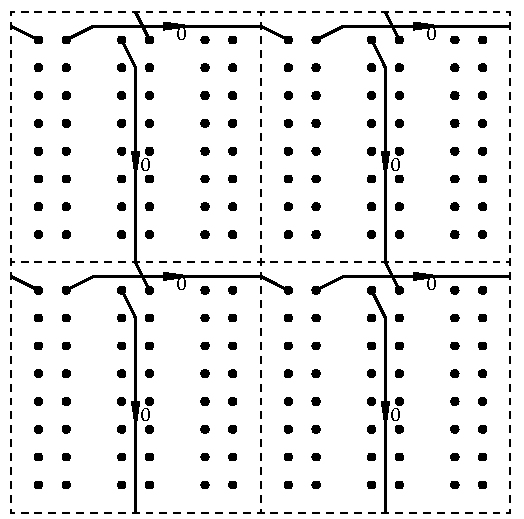
Connexion du fond de panier d'une boite CAM-8 pour une configuration infinie.
Seule une direction est montrée, sans bouclage aux bords.
| |
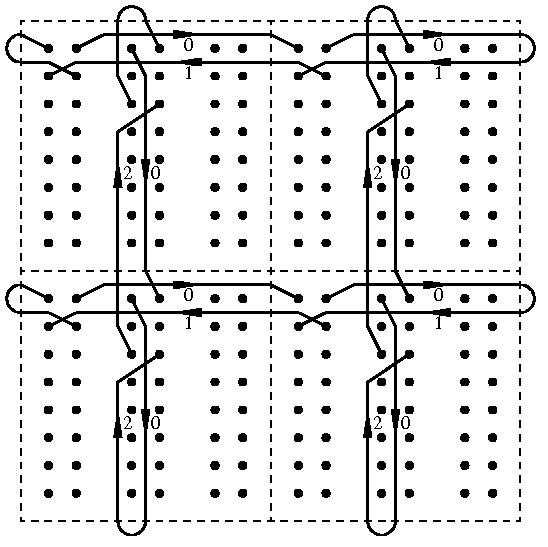
Connexion de 4 boites pour un tore 2D.
|
Comme pour le RAP-1, un moniteur externe permet de visualiser l'activité de la machine (c'est assez spectaculaire)
mais le plus complexe reste la configuration de la machine par l'hôte. Une suite de logiciels
est en développement depuis de nombreuses années. De nombreuses applications ont été démontrées
et la CAM-8 sert pour des recherches dans des domaines très variés mais l'interface est encore
rudimentaire.
La CAM-8 est très flexible. Il y a quelques limitations mais elles s'inscrivent dans
une architecture sophistiquée, destinée à simuler virtuellement des espaces jusqu'à
32 dimensions. L'espace mémoire est adressé dans chaque carte en associant un ou plusieurs bits
à une dimension, ce qui permet de créer des géométries quasi arbitraires où chaque longueur est une
puisance de 2 (256*256*256, 128*512, 4096*4096...).
Chaque carte effectue une consultation de table sur 16 bits pour chaque cellule mais
on peut effectuer des opérations plus complexes (consultation multiple, LUT virtuelle...).
Par exemple, pour le modèle FHP, les 16 bits peuvent servir pour représenter 2 sites à 1 bit par
directions ou 1 site à 2 bits par directions. Avec 8 cartes à 25 MHz, un boite CAM-8 soutient donc
400Mc/s en FHP3 ou 200Mc/s avec 2 bits par direction (Integer Lattice Gas à 2 bits).
Le voisinage est configurable site par site : une
carte peut accéder à des éléments non contigus dans la mémoire. Cela permet aussi bien
de calculer dans des espaces à N dimensions ou effectuer des interactions non locales.
C'est ce dernier détail qui fait une grande différence avec les autres machines.
Le site Internet du laboratoire de Norman Margolus n'est pas avare en détails techniques. On peut
y trouver les applications où la CAM-8 excelle et même un simulateur logiciel. Un article
[23] dans la
preprint archive montre une application de la CAM-8 aux simulations en 3 dimensions dans le
réseau FCHC à 24 bits. La capacité à effectuer des consultations successives de la LUT permet de
"casser" l'opérateur de collisions en isométries de 16 bits.
V.4 : EXA :
La société EXA a été créée par un professeur du MIT, Molvig. Elle utilise les techniques issues des gaz
sur réseaux dans les milieux industriels. Son nom vient de l'ordre de grandeur du même nom (mega, giga, tera, peta
puis exa). C'est le nombre d'opérations nécessaires pour des simulations réalistes en 3D, hors
de portée des ordinateurs classiques de l'époque (vers 1990).
EXA vend ses services aux sociétés qui ont besoin d'études sur des projets particuliers, dans les limites
permises par les modèles utilisés. Sa puissance de calcul consistait au début en une station Silicon Graphics
dotée de cartes accélératrices dotées d'ASIC traitant les calculs booléens. Le premier modèle (Molvig/Vichniac,
vendu sous le nom "DigitalPhysics") était une extension du modèle pseudo 4D avec 2 vitesses, soit un modèle
thermique avec 48 bits par site. Peu d'informations subsistent sur ce matériel qui souffrait des limitations
inhérentes aux modèle booléens.
Rapidement, la société a étendu ce modèle en utilisant la technique de Bolzman (BGK ?)
pour bénéficier de la montée en performance des calculateurs massivement parallèles
constitués de stations de travail (beowulfs). EXA développe, utilise et vend un logiciel
appelé Powerflow. Il existe peu de papiers décrivant le modèle utilisé mais l'approche choisie
est propriétaire (secrète) et utilise des astuces contestables pour augmenter artificiellement
le nombre de Reynolds simulable.
L'espace simulé est divisé en "voxels" (sous-divisions de l'espace 3D en cubes) de tailles variables dans l'espace
simulé. Cela permet d'adapter la quantité de mémoire et de calculs nécessaires en fonction de la vorticité locale.
La "granularité" sera beaucoup plus fine près des parois et dans les zones turbulentes. Certains
spécialistes ont objecté que cela brise la continuité du milieu et de ses propriétés, empêchant
les turbulences de se propager d'un voxel à un autre d'une taille (donc d'une viscosité) différente.
Les techniques qui y remédient sont secrètes et ne peuvent pas être examinées.
On pense que certains artifacts et défauts sont compensés par des marges de sécurité et une analyse
"intelligente" du partitionnement de l'espace. Une approche similaire au maillage dynamique ou progressif
(en cours du calcul) permet de réduire l'impact du problème dans une majorité des cas. Le reste est noyé dans
le bruit numérique et l'intégration lors des mesures. Enfin, cet inconvénient et les éventuels autres
problèmes sont souvent négligeables par rapport aux avantages, lorsqu'ils sont comparés aux techniques
classiques.
Les gaz sur réseaux n'ont pas d'avantage majeur en temps de calcul ou en utilisation mémoire
par rapport aux techniques établies, pour un cas identique. Par contre, la qualité des résultats
est souvent supérieure : ils sont fiables à quelques pourcents alors que les techniques classiques
sont fiables à quelques dizaines de pourcents. De plus, ils sont résolus explicitement dans le domaine
temporel, ils peuvent donc capturer la dynamique d'un problème qui n'apparaitrait pas autrement
(par exemple avec une résolution où le terme temporel est ignoré).
Ensuite, les résultats sont plus précis. Enfin, contrairement aux autres techniques, la simulation
n'a pas besoin de données issues de simulations réelles pour ajuster les résultats des calculs : il suffit
juste de fournir les géométries et les paramètres du fluide (Re et Mach) pour obtenir le résultat. Cette
dernière qualité a permis à EXA de se distinguer en résolvant des problèmes de turbulences complexes
inaccessibles aux autres méthodes. On comprend donc que les techniques employées
ne soient pas publiquement connues.
Le domaine d'utilisation reste limité au bas subsonique (inférieur à Mach 0.4), l'aéronautique n'est
donc pas la cible de l'entreprise. Les études portent sur les carénages et carosseries de motos, voitures,
camions, jusqu'à Re=6.10^6 avec un (très) gros serveur. Le domaine a récemment été étendu aux écoulements
internes et aux échanges thermiques. Il devient ainsi possible de simuler des injections de moteurs à
explosion ou des systèmes de climatisation.
Dans la pratique, cette qualité des calcul a un prix très cher en expertise et en temps CPU. Pour
donner un ordre de grandeur, un grand fabricant de voiture a décidé d'acheter un cluster de 256 stations
de travail dans le but unique d'utiliser Powerflow. Cette initiative a été suivie par la plupart des
constructeurs européens et américains. EXA loue aussi du temps CPU sur un cluster SGI Origin à 8 CPU
en mode batch (partagé entre plusieurs utilisateurs moins fortunés) et inaugure ainsi un nouveau mode
de "service commercial" sur Internet (la mode est vraiment au "e-business" bien que le travail par lot
ne soit pas une invention récente).
Peu de détails de programmation filtrent sur Internet ou sur le site web de la société. Une interview avec
un ingénieur français a cependant permis de dégager certains points. EXA utilise un réseau FCHC avec
des particules à trois vitesses (0, 1 ou 2 sites par pas de temps) en virgule fixe.
L'espace est divisé en "voxels" et en "surfels" de tailles variables (mais multiples
les unes des autres pour simplifier le pavage de l'espace). Chaque type de zone ("surfel" ou "voxel") est
traité par un code spécial. Un voxel utilise environ 130 octets de mémoire, un surfel en utilise 1300 et peut
représenter 12 ou 24 faces. Une simulation normale utilise facilement plusieurs millions de voxels, ce qui
nécessite l'emploi d'ordinateurs multiprocesseurs disposant de plusieurs gigaoctets de mémoire. Enfin, un
pas de temps équivalent à une seconde nécessite 22000 pas de temps de calcul.
La phase critique de l'expertise est l'adimensionnement : la détermination des paramètres de calcul
en fonction des paramètres réels. Le but est d'utiliser la puissance de calcul le plus efficacement possible.
Les paramètres importants sont la puissance de l'ordinateur (mémoire et vitesse), la vitesse du fluide
et la taille de l'éprouvette. La vitesse du fluide dans l'expérience doit être maximale (environ 0.3)
pour maximiser le nombre de Reynolds. Le nombre de Reynolds dépend aussi de la viscosité du fluide,
qui est fixe pour chaque voxel, et de la longueur caractéristique du problème. L'adimensionnement détermine
donc le nombre de voxels à utiliser en fonction de la définition du nombre de Reynolds et en ajustant
les termes de l'equation de Navier-Stockes aux équations caractéristiques du modèle avec les termes
non-linéaires qui apparaissent [26]. Le temps de calcul
dépendra du nombre de voxels, du nombre de pas de temps, de la complexité du fluide et du nombre de processeurs.
C'est un algorithme facilement parallélisable donc l'efficacité reste satisfaisante avec plusieurs centaines
de processeurs, comme le montre une fiche technique disponible sur le site web. Les plateformes de calcul
utilisées sont couramment Sun et SGI. Les résultats ou les vecteurs de calculs sont traités sur des stations
de travail graphiques déportées.
EXA a eu l'amabilité de communiquer un exemple de calcul réalisé en 1998 pour donner un ordre de grandeur
de l'efficacité du logiciel. Le calcul portait sur les turbulences autour de la carosserie
d'une voiture sportive afin d'évaluer l'efficacité de volets de déflexion. Cela a nécessité 22000 pas de temps
soit 4 jours sur un serveur à 8 processeur à 167 MHz avec 11 millions de voxels et 1 million de surfels.
Les entrées d'air ou les interactions des pneus n'ont pas été prises en compte mais le résultat est
saisissant.
Cette approche logicielle a beaucoup d'avenir car elle permet concevoir des véhicules plus silencieux
et moins turbulents sans louer ou construire des souffleries réelles (sans compter le prix de la maquette).
Powerflow permet de modéliser des turbulences liées aux aspérités d'une structure et donc de
vérifier son impact sur le bruit qu'il génère et sur le Cx de l'engin. Le temps de calcul peut être plus
court que la construction et les mesures d'une maquette dans une soufflerie silencieuse. Toutefois,
de nombreux problèmes subsistent comme la limitation de la taille des fichiers sur les systèmes
UNIX : la taille limite traditionnelle de 2Go est vite atteinte et les efforts de développement
sont encore en cours.
V.5 : "Fourmi" :
Ce projet du département MIME n'est pas encore opérationnel. L'architecture est simple dans les grandes lignes
et est entièrement dédiée aux automates cellulaires 1 et 2D, sans être spécialement prévue pour un usage précis.
Ce projet est appelé ainsi car il part du principe que l'union fait la force, comme dans une fourmilière :
une fourmi isolée n'est pas très productive alors qu'une armée de fourmis peut effectuer beaucoup de travail.
C'est une architecture extensible par addition de modules : le prototypage s'effectue avec
un seul module puis d'autres modules seront construits en nombre (donc moins chers à l'unité) lorsque la
technique est au point.
La "fourmi" est une machine SIMD divisée en deux : elle dispose d'un séquenceur (partie contrôle)
et d'une ou plusieurs cartes d'exécution. Chaque élément est configurable : le séquenceur est câblé
et "exécute" un programme chargé en SRAM locale, tout en envoyant des signaux aux parties d'exécutions.
Chaque carte "active" est composée essentiellement d'un FPGA et d'un bloc de DRAM adressée par le FPGA.
Le FPGA est en technologie SRAM, il peut être reconfiguré à tout moment par l'ordinateur hôte (Sun SPARC).
Les fonctions réalisables sont donc potentiellement infinies mais limitées par la taille et l'architecture
du FPGA ainsi que par son langage de commande : le projet Fourmi a aussi pour objet de développer un langage
de description des automates cellulaires. Le tout fonctionne à quelques dizaines de mégahertz.
La pratique est beaucoup plus complexe, comme le confirme la durée du développement. Le programme
de commande traduit le langage de description en code VHDL, ce qui est loin d'être facile. Le bus VME,
autour duquel est architecturée la machine, ne permet d'envisager qu'une dizaine de cartes au maximum.
Les cartes sont reliées par un réseau unidimensionnel. Le développement est freiné par le manque de moyens
matériels, par le peu de personnes travaillant au projet et par la dépendence envers les fabricants de FPGA :
de nouvelles versions de FPGA et de logiciels apparaissent plus vite que le projet et il est difficile
de conserver d'anciennes versions car elles ne sont plus supportées.
La CAM-8 a échappé à ces problèmes : la topologie est beaucoup plus flexible et en 3D, laissant envisager
la construction de cubes de dizaines de boites de côté (le problème est alors la dissipation thermique...).
Le projet CAM-8 bénéficie aussi de subventions du département de recherche de l'armée américaine, ce qui
permet de résoudre certains problèmes de manière plus triviale que lorsque le budget est dépassé ou inexistant.
V.6 : Carte ISA :
Ce chapitre présente la première étude personnelle de matériel dédié au calcul de gaz sur réseau hexagonal,
vers 1996, après la sortie de l'article de l'annexe B. Aucun accélérateur de cette structure n'a jamais
été réalisé. Le but était principalement d'effectuer les calculs
et les mouvements complexes de données par de simples circuits électroniques sur une carte ISA avec
un budget très restreint. La plateforme cible était un i286 à 12MHz doté d'un bus ISA 16 bits. La vitesse
théorique est donc limitée par la vitesse du bus ISA et la taille des expériences est limitée par le
x86 en mode réel (64Ko).
La structure de la carte est dérivée d'une étude des mouvements de données dans l'algorithme de l'annexe B.
La carte ne pouvait être dotée de mémoire spacieuse, elle devait donc dépendre de la mémoire centrale de l'hôte.
Les composants doivent être simples, économiques et peu nombreux, sur un circuit imprimé à 2 faces
dessiné à la main. Aucune exploitation des résultats n'était prévue : pas de sommation car les particules
étaient organisées en multisite et l'affichage était contrôlé par la palette de la carte VGA.
L'étude des dépendances des données a permis de définir une stratégie : seules quelques lignes ont besoin
d'être mémorisées dans la carte, ce qui permet de ne contenir que quelques dizaines de kilooctets de SRAM
ou de FIFO. Dans ce cas, le plus difficile est de synchroniser le contenu des différentes mémoires : il faut que
le logiciel collabore étroitement avec la carte pour permettre à l'algorithme de fonctionner correctement.
Le schéma suivant décrit les dépendances de données :
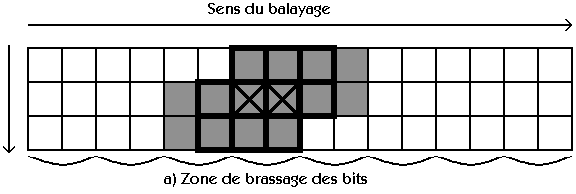
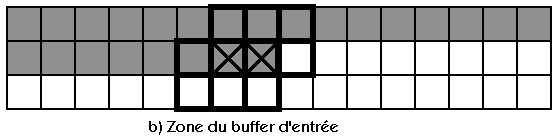
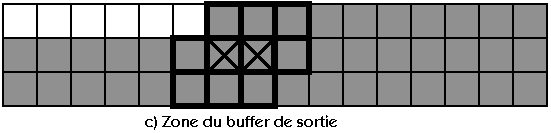
Description des dépendances de données pour le modèle multisite
Comme les mots transmis sont larges de 16 bits et puisque la gestion des lignes paires/impaires est
inutilement complexe, le réseau a été tourné à 90 degrés et les noeuds sont traités par paires.
Il faut donc 2 LUT et chaque cycle d'horloge traite deux sites. La figure suivante montre le nommage des
directions, similaire à la stratégie du deuxième code de référence :
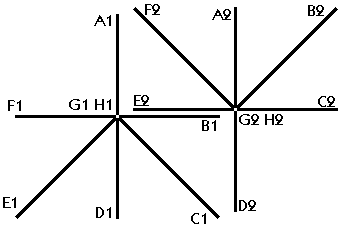
Deux stratégies existent : utiliser des FIFO ou des SRAM. L'étude a porté d'abord sur les FIFO.
Par convention, N sera le nombre de sites par ligne.
L'ordinateur et la carte sont asynchrones, l'ordinateur doit partager la bande passante entre le flux entrant
dans la carte et le flux sortant. Pour des raisons de simplicité, la gestion de la DMA n'a pas été envisagée.
Le programme de l'ordinateur hôte est assez simple : il envoie un bloc puis en reçoit un autre
à mettre au même endroit. Il faut vérifer à chaque fois que le buffer que l'on va accéder est prêt,
grâce à des sémaphores prévus à cet effet. La boucle interne doit être écrite en assembleur car
elle utilise des instructions spéciale rep insw et rep outsw qui ne sont pas disponibles
dans les langages de haut niveau :
; init de la boucle externe :
push ds ; ds pointe vers le tableau
pop es ; ds = es = début du tableau
xor di,di ; di = 0
xor si,si ; si = 0
mov dx,inout_port ; adresse de la carte ISA
mov bx,nb_lignes
loop_bx:
; synchro 1:
add dx,2
loop_dx1:
in al, dx
and al,1 ; vérifie que le buffer d'entrée est prêt
jz loop_dx1
sub dx,2
mov cx,N/2
rep outsw dx,si ; bloc DS:SI vers port DX
; synchro 2:
add dx,2
loop_dx2:
in al, dx
and al,2 ; vérifie que le buffer de sortie est prêt
jz loop_dx2
sub dx,2
mov cx,N/2
rep insw dx,di ; port DX vers bloc ES:DI
dec bx
jnz loop_bx
; fin
|
Dans cet exemple, les phases sont synchronisées en utilisant un port de contrôle,
permettant de lire l'état interne de la carte. Nous allons voir plus loin qu'il est possible de
s'en passer. La synchronisation entre le processeur et la carte peut être gérée par exemple en insérant
des wait states sur le bus lors de la lecture et de l'écriture du port.
Il faut aussi une période d'amorce du "pipeline" interne de la carte mais ce n'est pas
traité ici.
Si le processeur envoie 2 octets par cycle, s'il faut 2 cycles par site (écriture puis lecture) et si
le bus envoie 16 bits par cycle en rafale, la bande passante maximale théorique est de 12MHz/2*2 soit
12 millions de sites par seconde à 12 MHz. Les aléas du bus ISA abaissent ce débit dans la pratique,
en particulier pour accéder à la mémoire DRAM lente et pour garder la compatibilité avec les cartes ISA
8 bits. Il faut en théorie 2 cycles pour un accès 16 bits et 3 cycles pour deux accès 8 bits en mode
16 bits. Cela donne beaucoup de temps à la carte ISA pour traiter les informations par paquets 16 bits,
à 6 MHz maximum en théorie. Le chemin critique de l'accélérateur dispose donc de 160 ns au minimum
pour effectuer son travail, ce qui est peu contraignant. Le processeur effectue deux fois plus de travail
de mouvement que la carte elle-même car sa bande passante est partagée par plusieurs flux : la carte
doit donc pouvoir garder en mémoire deux lignes (2*N sites) au minimum pour éviter de perdre des données.
En utilisant des FIFO toutes faites, on gagne en simplicité de gestion : pas d'adressage de SRAM à générer.
La figure précédente dit en a) qu'il faut conserver pour le buffer d'entrée 2N sites, soit 2 FIFO de
N octets. Une ligne doit être constament gardée en matériel afin de simplifier le logiciel et les pointeurs.
La deuxième se vide au fur et à mesure que le calcul avance.
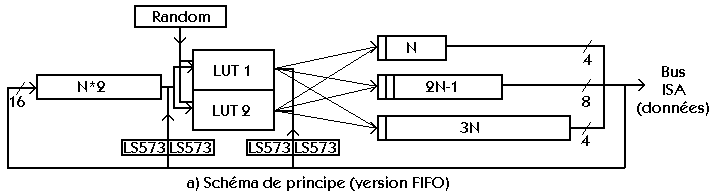
Le calcul donne 4 bits pour la première ligne, 8 bits à la suivante et les 4 derniers pour la troisième
ligne. De plus, de petits buffers doivent être correctement placés pour temporiser certains résultats de
un ou deux cycles. On modifie donc la structure de la figure a) pour exploiter des FIFO sur 8 ou 16 bits :
on utilise des bits indépendants dans la même FIFO puisque tous les flux sont synchrones. Il faut donc trois
étages de FIFOs à N étages, ou en tout 4 FIFOs de N octets. Dans la versions a), on s'aperçoit aussi que
le calcul s'effectue à chaque lecture d'un mot en sortie : on peut donc économiser un étage de FIFO.
Les parties délicates sont la programmation des LUT, la gestion du "mélange" des bits et les buffers
associés, ainsi que le contrôle général de la carte, non représenté ici. Le générateur de nombres aléatoires
peut être implémenté dans une simple PAL avec un registre à décalage à rétroaction linéaire.

Une autre optimisation porte sur l'utilisation des circuits : on peut réduire le nombre de circuits
buffers 8 bits (des bascules latch non transparentes) à seulement deux en traitant les bits indépendamment.
Certains bits peuvent donc être utilisés à différents degrés de délai et il n'y a pas de broche inutilisée.
Ainsi, quatre circuits suffisent à "brasser" les bits, le reste du circuit imprimé doit gérer les autres
fonctions : accès aux LUT pour leur configuration, décodage du bus ISA, synchronisation et validation
des horloges de tous les circuits. Ce sont ces parties qui sont les plus complexes et qui sont susceptibles
de demander du temps pour la mise au point.
L'architecture décrite dans ce chapitre n'a pas été implémentée pour des raisons financières, de temps,
de moyens mais surtout parce que les programmes qui ont été développés ensuite sont beaucoup plus rapides
que les 12Mc/s théoriques que l'accélérateur permettait d'atteindre. La version à base de SRAM pour émuler
les FIFOs (chères, voir RadioSpares) est plus compliquée car il faut adresser des SRAM : les composants
discrets sont trop nombreux, les PAL sont trop petites et les FPGA dépassent le budget.
V.7 : Anneau de strip mining :
L'idée de cette architecture est venue dans une discussion, à la fin d'une présentation par Amal Stri du
projet Fourmi en 1998. C'est une application directe du principe de "strip mining" utilisé dans le programme :
il y a deux niveaux de mémoire de vitesse et de quantité différentes afin de diminuer le coût total
du système. Une mémoire de type DRAM est à la fois spacieuse et économique, elle est ici contrôlée par une puce
spéciale qui effectue le rafraîchissement et le transfert de blocs, alternant lectures et écritures en rafale.
Ensuite, chaque "ligne" de strip mining est implémentée par un circuit qui peut être répliqué à volonté
selon les besoins et le budget. Il peut consister en un gros FPGA ou tout simplement correspondre au circuit
décrit dans le chapitre précédent.
Ce type d'architecture a un intérêt particulier : plus le nombre de circuits de calcul de lignes est grand,
plus le calcul est rapide, indépendamment de la taille du tableau à calculer. La partie calcul est séparée
de la partie stockage et chacune peut avoir la taille désirée. Il devient possible d'augmenter le
nombre total de sites calculables en ajoutant une barette de DRAM disponible dans le commerce, ou d'augmenter
la vitesse de calcul en fabricant d'autres cartes de calcul. Le contrôleur de DRAM peut aussi gérer des
communications plus lentes afin d'inclure l'anneau dans un anneau plus grand et implémenter une architecture
de strip mining du deuxième ordre (avec un anneau d'anneaux).
L'affichage du résultat peut être effectué en lisant le trafic sur un des liens et en envoyant le flux vers
un tampon d'affichage pour le synchroniser avec le balayage de l'écran. Il faut donc que le flux de l'anneau
contienne un "jeton" indiquant un retour de balayage vertical mais il est plus simple de gérer ce cas
directement avec le contrôleur de mémoire : il doit contenir les pointeurs de début et de fin du balayage
de la DRAM et peut donc générer le signal de synchronisation sans complexité inutile.
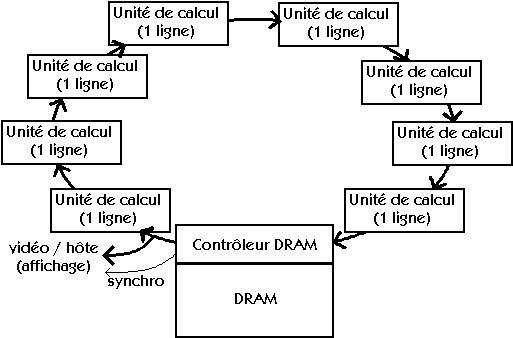 Une autre caractéristique intéressante est que l'anneau est unidirectionnel : chaque module a besoin
d'un port d'entrée et d'un port de sortie identiques dont la bande passante (largeur et fréquence) correspond
à la vitesse de calcul de chaque unité (la vitesse est la même pour un système synchrone). Le contrôleur de
mémoire doit donc contenir deux mémoires tampons afin de garder un flux de données constant malgré l'accès
alterné (R/W) à la DRAM.
Une autre caractéristique intéressante est que l'anneau est unidirectionnel : chaque module a besoin
d'un port d'entrée et d'un port de sortie identiques dont la bande passante (largeur et fréquence) correspond
à la vitesse de calcul de chaque unité (la vitesse est la même pour un système synchrone). Le contrôleur de
mémoire doit donc contenir deux mémoires tampons afin de garder un flux de données constant malgré l'accès
alterné (R/W) à la DRAM.
Ce type de système parallèle exploite les caractéristiques du modèle calculé et son extensibilité est différente
comparée aux autres systèmes cellulaires. D'habitude la puissance est augmentée en ajoutant des modules
qui contiennent à la fois de la mémoire et des circuits de calcul mais le prix de la DRAM au mégaoctet est
beaucoup plus faible que de la SRAM de petite quantité. L'accès par blocs dans ce modèle est aussi
un facteur qui rend cette architecture possible : des accès aléatoires pénaliseraient la bande passante
à cause de l'interface compliquée des puces de DRAM. Ce système peut donc être étendu par ajout de composants
mémoire économiques et par ajout de modules de calcul (circuits imprimés ou FPGA).
Le problème de cette approche, malgré le rapport performance/prix intéressant, est qu'il est limité aux
modèles à interactions courtes en 2D (voisinage de Moore ou de Von Neumann par exemple). Il ne peut être
utilisé pour des modèles uni- ou tridimensionnels et l'intérêt est réduit en dehors des gaz sur réseaux :
ce n'est pas une architecture "généraliste". Si le domaine à étudier est limité aux LGA 2D, c'est
l'architecture parallèle la plus recommendée, même avec des modèles non binaires : ILG, BGK...
V.8 : tableau de PAL :
L'exploration suivante est un "exercice d'école" destiné
à comprendre à quel point le modèle physique influence l'architecture
matérielle. Les contraintes de prix, de flexibilité et de réalisation
sont ensuites utilisées pour modifier les choix.
Commençons par un cas de figure "idéal" car il représente exactement le modèle FHP : chaque site est
associé à un circuit logique programmable, par exemple une PAL 16L8.
\ / \ / \ / \ / \ / \ / \ / \
--- PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL
/ \ / \ / \ / \ / \ / \ / \ /
PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL ---
\ / \ / \ / \ / \ / \ / \ / \
--- PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL
/ \ / \ / \ / \ / \ / \ / \ /
PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL ---
\ / \ / \ / \ / \ / \ / \ / \
--- PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL
/ \ / \ / \ / \ / \ / \ / \ /
PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL ---
\ / \ / \ / \ / \ / \ / \ / \
--- PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL
/ \ / \ / \ / \ / \ / \ / \ /
PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL --- PAL ---
|
Chaque lien correspond à deux connexions (un bit dans chaque sens). Ce système pourrait
fonctionner à 20MHz : le parallélisme massif permet d'atteindre environ 1Gc/s avec la
configuration de circuits ci-dessus (un carré de 8 par 8).
La performance dans des applications réelles (500*500 environ) serait donc impressionnante
mais les obstacles pratiques sont très nombreux :
il faudrait un nombre considérable de circuits, sur une surface gigantesque
(proportionnelle au nombre de sites)
la visualisation serait difficile (avec des LED ?)
les essais avec les compilateurs VHDL ont montré que la complexité des équations ne
permet pas de programmer une PAL normale avec les règles FHP-3 "saturées"
les "obstacles" (murs) seraient soit câblés par des fils, soit programmés dans les PAL,
mais ne pourraient pas être modifiés facilement et rapidement
l'arbre de l'horloge serait lourd à gérer ; il faut faire
un arbre binaire pour répartir le signal d'horloge de manière
synchrone sur tout le circuit (comme expliqué dans la documentation de la CAM-8).
la propagation de la valeur du générateur de nombres aléatoires est aussi
complexe que la propagation de l'horloge dans le circuit.
Finalement, cette approche est réservée à des cas très particuliers où l'investissement
en matériel est justifié par une utilisation intensive, hors du cadre de la recherche.
Une puce VLSI avec un réseau de 16 * 16 sites pourrait servir de base à des générateurs de
nombres pseudo-aléatoires (de probabilité 2/7) contrôlés par clé.
Une alternative serait d'utiliser des mémoires SRAM rapides comme celles
utilisées dans les caches L2 des PC. Elles sont relativement économiques,
largement répandues et ne sont pas limitées par la complexité de l'équation.
Par exemple, partons de mon stock personnel : environ 100 SRAM 62256 15ns
en boîtier DIL étroit 28 broches, toutes récupérées sur des cartes mères défectueuses.
Comme leur contenu peut être changé à tout moment,
le système simulé peut être intéractif. Une SRAM de 32 Koctets
contient plus de données que nécessaire pour une seule table (512 octets),
un boîtier peut donc en plus contenir les informations de 64 lignes différentes
pour lesquelles les informations ne seraient pas homogènes (comme pour des parois
plus ou moins glissantes, de informations sur la géométrie...). Il faudrait alors que l'hôte
optimise l'allocation de ces sous-tables mais ce n'est pas un problème inquiétant.
La mémoire est organisée par octets et les murs peuvent être traités séparément, il
reste donc un bit libre dans les données, utilisable pour implémenter FHP4 :
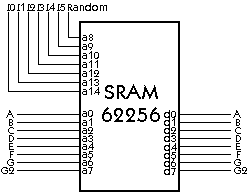
Il n'y a pas assez de puces pour constituer un tableau entier (un tableau de 10 par 10 n'est
pas intéressant pour des applications normales), il faut donc balayer la surface ligne par ligne.
Là encore, une ligne de 100 sites n'est pas assez pour des cas classiques, il faudra donc plusieurs
cycles pour balayer une ligne réelle. L'organisation des circuits est toutefois 1D : tous les circuits
sont placés en ligne. Cela pose un gros problème : il faut mémoriser les autres lignes, une moitié des
puces mémoire sera alors dédiée à cette fonction et il faudra les adresser séparément. Le tableau peut
donc contenir 50 x 32K = 1,6 millions de sites qui peuvent être organisés par groupes de 50 sites.
Une autre solution serait d'acquérir 100 puces FIFO de plusieurs milliers d'octets chacune pour simplifier
l'adressage et le câblage mais ce sont des pièces chères. Le "brassage" des bits pour les répartir sur
plusieurs ligne consécutives peut s'effectuer comme avec la carte ISA, avec des buffers discrets.
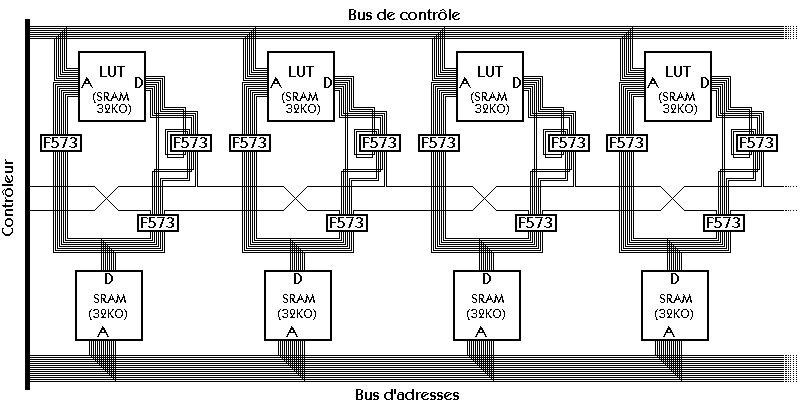
Le problème le plus inquiétant est la programmation les SRAM : il faudrait intercaler des transmetteurs
qui sélectionnent la provenance des données dans le chemin critique,
ce qui diminuerait la vitesse, augmenterait le coût et la consommation
électrique. De toute façon, la sortie de ces puces mémoires n'est pas "latchée"
(la sortie ne peut être maintenue lorsque que l'entrée change).
Un système synchrone rapide n'est donc pas possible car il faut en plus
alterner les cycles de lecture et d'écriture des SRAM de stockage. On peut considérer que
la vitesse de consultation des LUT est de 15 ou 20 MHz, soit environ 1 milliard de sites par seconde
avec 100 puces de SRAM. La consommation électrique est au minimum de :
100mA sous 5V x 100 = 50 Watts pour les SRAM seules.
La question reste en suspens, mais il est évidemment plus facile de
programmer un ordinateur "classique" que de mettre au point un
système de ce style, même avec des FPGA modernes, en maintenant des
performances et une flexibilité similaires.
Il apparaît que la création d'une machine dédiée au calcul de FHP n'est pas aussi aisée que
le modèle le laisse penser au départ. L'électronique "câblée" reste pourtant le dernier recours lorsque
la vitesse demandée justifie le manque de flexibilité et le budget consacré au projet. L'approche
parallèle en 1D ou en 2D permet de gagner un ordre de grandeur dans la vitesse de calcul. Une machine à base
de dizaines d'ASIC est une solution brute à un problème très précis mais la nature des circuits intégrés
implique une perte de vitesse dès qu'il faut communiquer avec un circuit intégré voisin : une broche
suivie d'une piste de circuit imprimé constituent une charge capacitive qui devient prépondérante à très
haute vitesse. Il serait donc illusoire de croire à une augmentation linéaire de la vitesse de traitement
lorsque l'horloge est accélérée : un système synchrone basé sur l'architecture PAL ou sur un tableau d'ASIC
sera limité par la vitesse de communication entre les puces. Malgré ses avantages, le calcul "câblé"
sera donc toujours limité par les constantes fondamentales de la physique (comme la vitesse de la lumière ou
la mobilité des électrons).
V.9 : Conclusion :
Il semble que l'avenir de ce type de machines se trouve dans les réseaux logiques
reconfigurables sur site : les FPGA. Les nouvelles générations sont très, très rapides et
peuvent même contenir des microprocesseurs. Leurs architectures, comme pour les microprocesseurs,
deviennent de plus en plus complexes et il est difficile de les utiliser à 90% de leur
capacité théorique, sans parler du manque de transparence des constructeurs, du
prix élevé des logiciels et de plateformes... Le projet Fourmi a exploré ces différents problèmes.
Cependant les FPGA offrent un niveau d'abstraction qui permet de faire bénéficier l'utilisateur
des performances d'une nouvelle plateforme au prix d'une recompilation du source VHDL ou Verilog.
Des plateformes diverses existent déjà, allant de la simple carte PCI aux systèmes massivement
parallèles. Ces systèmes reconfigurables se démocratisent (lentement mais sûrement) car ils
touchent beaucoup plus d'applications : ils permettent de calculer rapidement tout ce qu'un
ordinateur classique peut calculer. L'ordinateur "hôte" se charge des tâches complexes, de l'interface
avec l'extérieur, de la configuration, pendant que la partie de "calcul brut" est prise en charge par le
système reconfigurable.
Il faut toutefois remarquer qu'aucun standard n'existe actuellement. On peut spéculer sur l'utilisation
du VHDL pour programmer des automates cellulaires, Cellang n'a qu'un usage très restreint et le reste
reste au stade expérimental. Dans l'absence d'un outil déterministe et fiable pour programmer les
FPGA, le précieux matériel risque d'être sous-utilisé comme un ordinateur classique. Doit-on en venir
aux ASIC ? C'est ce que prépare Norman Margolus [30] avec une puce mélangeant
circuits de mémoire et de calcul, bénéficiant ainsi des toutes dernières technologies.
Les réseaux d'interconnexion entre les processeurs élémentaires sont très divers. Pour calculer des
gaz sur réseaux en 2D, la méthode la plus pratique, économique et extensible est l'anneau
décrit au chapitre 6. Les autres techniques semblent soumises aux caprices des évolutions technologiques.
Les calculs en 3D sont moins faciles à câbler de manière flexible, il faut encore attendre que la
technologie évolue. Un hypercube 4D semblerait convenir mais la seule expérience effectuée a utilisé
une CAM-8. Les architectures adaptées aux réseaux en 2D ne peuvent pas être étendues directement à la 3D
car c'est une projection d'un réseau 4D. De nombreuses recherches supplémentaires doivent être effectuées pour déterminer
une architecture adaptée mais les techniques futures seront certainement extrapolées à partir des techniques 2D
comme l'anneau (issue de l'algorithme de strip mining).
Conclusion
Le travail effectué pour ce mémoire est une source d'enrichissements et
de surprises inépuisables, dans des proportions imprévues au départ.
L'annexe D montre que les programmes FHP, même les plus évolués,
sont loin de se mesurer avec le programme développé dans ce mémoire,
espérons donc que ces enseignements profiteront à de nombreuses personnes.
Une conclusion simple et concise n'est pas possible car les remarques sont
trop nombreuses. Au contraire, essayons de les placer dans un contexte plus général.
Commençons par résumer les innovations dont chacun devrait tenir compte lors de la
programmation de codes FHP ou similaires.
1 : Avancées pour le domaine des gaz sur réseaux
1.1 : Approche globale du problème :
Programmer des LGA ne se limite pas en l'expression d'un algorithme dans un langage particulier :
le premier problème à surpasser avant de concevoir un programme efficace est de s'affranchir du
niveau conceptuel des langages textuels. Bien que le premier charme des LGA soit d'être programmables
"facilement", on vérifie aujourd'hui que les algorithmes "naïfs" ne sont plus adaptés aux ordinateurs actuels
(à partir de 1995 environ) et nécessitent une connaissance approfondie du modèle physique
et de l'architecture de la machine.
Pour programmer les LGA, il faut partir du modèle physique exprimé abstraitement, examiner de nombreuses
options et comparer leurs intéractions dans un cadre choisi. L'interface entre le logiciel et le matériel,
qui permet de contrôler la performance du programme, s'étend sur le système d'exploitation, sur l'algorithme,
le modèle physique, l'application, la machine cible... Ce sont autant de détails, parfois contradictoires,
qu'il faut considérer attentivement, longtemps avant de fixer des choix définitifs ou commencer à programmer.
La philosophie de programmation joue aussi un rôle important : selon les objectifs, les moyens et les
connaissances, des niveaux différents de performance pourront être atteints. Les objectifs doivent être
réalistes et les moyens doivent être préalablement maitrisés, sinon le projet risque de ne pas aboutir.
Il ne faut pas hésiter à constituer une large base de connaissances (bibliographie, discussions, rencontres,
butinage sur Internet) afin de maitriser le sujet dans ses nombreux détails.
Lorsque suffisament d'éléments sont réunis et préparés, l'intransigeance et le souci du détail permettent
de consolider l'édifice, qui ne manque pas de montrer des signes de faiblesse à mesure qu'il s'agrandit.
La cohérence du programme devient de plus en plus difficile à gérer lorsqu'on ajoute des éléments :
s'il y a N éléments dans un programme, l'ajout d'un autre élément nécessite N vérifications qui peuvent
remettre en cause d'autres éléments. Le développement logiciel de ce projet a d'ailleurs été interrompu
car il y a trop de parties à réécrire et les outils actuels ne permettent pas de les développer suffisamment
rapidement. Ce n'est pas un problème lié au langage assembleur car des intéractions complexes apparaissent
dans tous les langages.
La programmation d'un logiciel optimisé n'est pas seulement un travail de science fondamentale :
ce mémoire a fait appel à des compétences en électronique, compilation, système d'exploitation.
Il emprunte des méthodes utilisées entre autres par les codeurs de jeux vidéo, qui ont comme préoccupation
commune l'utilisation la plus efficace possible de chaque ressource de l'ordinateur. Il faut pourtant
faire attention aux parties théoriques car le résultat risque d'être inutile : l'utilisation du modèle
FHP en dehors de ses limites raisonnables donne des résultats aberrants. L'utilisation d'un modèle trop
primitif semble économique en complexité de calcul mais est sous-efficace en temps de calcul total sur la
machine... Un codeur de jeu vidéo sera plus intéressé par l'effet visuel que par l'exactitude d'un calcul.
Pour résumer, il faut entre autres : être très attentif, être compétent dans de nombreux domaines,
pouvoir faire le lien abstrait entre chaque partie, travailler à la fois sur le très haut et le très
bas niveau. En réduisant le nombre de contraintes (par exemple : temps du projet trop court, moyens
trop réduits, ressources trop faibles) il est possible de faire des programmes de meilleure qualité
mais cela est rarement le cas car une contrainte est souvent compensée par une autre.
1.2 : Organisation des données :
La refonte de la structure des données et des algorithmes (principaux et annexes) est souvent la
première voie à explorer pour améliorer fondamentalement un programme.
Dans le contexte d'une approche globale,
c'est à dire en tenant compte des détails d'implémentation, il faut essayer et comparer les différentes
possibilités qui existent. Lors de ce projet, quatre organisations ont été examinées et on peut résumer
leurs propriétés dans le tableau suivant :
|
type
|
avantage(s)
|
inconvénient(s)
|
tableau 2D d'octets
(LUT, multisite)
(chapitre III.4)
|
simplicité de progammation/compréhension,
adapté pour les ordinateurs 8/16 bits (ex.: i286)
|
sous-efficace pour les microprocesseurs récents
(mots large, coeurs OOO, occupation de la cache...)
|
tableau 2D de mots
/ 4 sites sur 32 bits
(multisite à traitement parallèle)
(chapitre III.6)
|
plus efficace pour les coeurs 32 bits (i386-486-P53C),
moins d'instructions pour le mouvement de bits individuels
|
plus de manipulations d'octets individuels,
donc plus contraignants pour les coeurs récents
|
multispin entrelacé dans un tableau
(chapitre IV.4)
|
convient le mieux aux microprocesseurs modernes
(registres larges, OOO, cache sur la puce)
|
complexe
(mais ce mémoire montre que c'est possible)
|
|
multispin (equation booléenne) sur
plusieurs tableaux séparés
|
convient naturellement aux calculateurs vectoriels
|
nécessite trop de pointeurs (pression sur les registres
et le compilateur pour les processeurs classiques,
mauvaise localité spatiale, risque de cache thrashing
avec certaines granularités)
|
Puisque l'étude porte sur les microprocesseurs modernes (Pentium MMX et Pentium II)
il est donc recommandé d'utiliser la technique "multispin entrelacé" sur ces
plateformes. Les autres techniques sont sous-efficaces, mettent une pression inutile
sur l'allocation des registres (pointeurs et données) et utilisent mal la hiérarchie
de la mémoire.
De plus, il est fortement recommandé d'utiliser des buffers temporaires comme
décrits dans au chapitre III.3, afin d'éviter une occupation trop importante. Même si cela peut
paraître peu important sur des ordinateurs actuels disposant d'au moins 64MO de mémoire,
l'espace supplémentaire nécessaire à la collecte des statisques compense vite cette économie.
De plus, le léger surcoût en complexité de programmation est justifié par une meilleure
utilisation de la bande passante vers la mémoire. Par exemple, la stratégie de write
back du Pentium est no-write-allocate : elle court-circuite la cache si la
zone mémoire n'est pas déjà cachée, ce qui pénalise certains algorithmes selon leur
ordre de lecture/écriture.
1.3 : Strip mining :
L'utilisation du strip mining dans le projet permet de gagner entre 25 et 50% du temps de
calcul selon la taille des tableaux, alors même que le coeur du CPU est
saturé par les calculs. Plus qu'une simple "astuce", cela montre bien que les
microprocesseurs sont très dépendants de la localité spatio-temporelle des données car
toute leur hiérarchie mémoire est conçue selon ce postulat optimiste.
Les premiers microprocesseurs ne disposaient pas
de mémoire cache, et les machines dédiées ont des canaux spécialisés qui garantissent
une certaine bande passante, mais les microprocesseurs actuels ont une bande passante
vers la mémoire centrale qui est très réduite par rapport à leur fréquence de fonctionnement
interne. A mesure que les architectures deviennent plus complexes, de nombreux paramètres
rendent le travail plus difficile : il faut faire attention à la cachabilité des
zones accédées, aux temps de latence, aux transferts par paquets,
à l'ordre et à l'alignement des accès...
En concevant un algorithme, il faut donc absolument tenir compte de ces paramètres, avec
la difficulté supplémentaire de la nature des traitements à effectuer. En effet, la fenêtre
de strip mining doit respecter certaines propriétés spatio-temporelles (qui étaient mal identifiées
au début du projet). D'autres types d'automates cellulaires, des traitements de signaux
(images, sons) ou des opérations mathématiques complexes (inversions de matrices) ont des dépendances
différentes entre les données et nécessiteront un algorithme de strip mining différent, qu'il faudra analyser
sérieusement pour éviter que la mémoire centrale ne ralentisse le processeur.
En règle générale, on peut considérer que tout balayage d'un tableau avec des intéractions
limitées aux voisins peut et doit bénéficier du strip mining.
Il faut espérer que les prochaines générations de microprocesseurs banalisent encore plus
les instructions dédiées au contrôle de la mémoire cache. Le strip mining présenté ici
est au départ un palliatif au manque d'instruction spéciale et fonctionne par "cache touching"
(une partie de la ligne de cache est accédée, le reste est ensuite utilisé au maximum et on attend
que le mécanisme de LRU vide la ligne automatiquement). Une amélioration simple consisterait à
effectuer le travail de LRU grâce à une instruction explicite et gagner ainsi quelques
pourcents sur l'espace réellement utilisé dans la cache (pour être remplacée, une ligne doit être
inutilisée, elle prend donc de la place inutilement) et donc accélérer la vitesse du programme.
Jusqu'à maintenant, la seule instruction disponible (WBINVD) vidait indifféremment toute la cache et
ne procurait aucun bénéfice net (voir les tests en annexe C). Intel a amélioré la situation lors de
l'introduction du Pentium III et des instructions SSE, on peut donc espérer que les prochaines
versions du programme en bénéficieront.
Le Pentium II avait déjà changé le "paysage" de la mémoire
cache par une architecture à bus séparés très efficaces et rendait ainsi la L2 presque aussi "rapide"
que la L1. La mémoire principale n'avait pourtant pas été accélérée mais le schéma original
de strip mining fonctionne très bien. Les choses se compliquent dans les cas où la taille des
simulations nécessite l'emploi de liens encore plus lents : réseau local Ethernet ou disque dur.
Il faut alors utiliser le strip mining au deuxième degré : la complexité et le gain de cette technique
éprouvée au niveau de la carte mère peuvent être retrouvés au niveau d'un système à une échelle différente.
Des études sont en cours pour le projet beo-kragen.
D'une simple réorganisation des ordres d'accès
à la mémoire, le point de vue a évolué vers la gestion de tampons mémoire et de flux de données à l'échelle
du système entier, prouvant que le programme est actuellement étudié à un niveau d'abstraction beaucoup
plus élevé qu'à l'origine.
1.4 : Parois complexes :
L'utilisation de listes de modifications pour gérer les parois permet de bénéficier de toute la
puissance intrinsèque du modèle FHP. Bien que cela soit plus difficile à programmer, les efforts
sont justifiés par une grande flexibilité des parois tout en ayant une occupation raisonnable en
temps CPU et en mémoire. Le projet a permis de programmer et de résoudre les couches de bas niveau,
le reste de l'effort étant laissé à la discrétion d'autres programmeurs spécialisés dans d'autres
disciplines (l'algorithme de Bresenham dans un repère rhombohédrique
ne faisant pas l'objet de ce mémoire). Ce projet de maitrise
prouve que les listes de modifications sont possibles et montre comment les réaliser
(bien qu'on puisse toujours améliorer la technique). Il existe aujourd'hui moins de raisons de s'en passser.
1.5 : Programmation en assembleur :
La pratique de l'assembleur est souvent vue comme un exercice de haute voltige, inutile et peu pratique.
Ce mémoire montre que ce n'est qu'une des nombreuses difficultés que l'on rencontre dans les exercices
de programmation courante car la plus grande difficulté est souvent au niveau algorithmique (le coeur
du calcul utilise un nombre très réduit de types d'instructions, ce qui invalide l'argument
de complexité). Le reste de la "difficulté" est au niveau de
l'interface, ce qui peut être résolu par de nombreux moyens autres que celui utilisé ici.
L'utilisation de l'assembleur ici correspond à une philosophie de contrôle total sur les instructions
que le microprocesseur va exécuter, et donc maitriser étroitement la performance du programme,
quasiment au cycle près. Aucun autre moyen n'existe actuellement pour garantir la "pureté"
d'un code exécutable. Les meilleurs compilateurs du monde ne permettent qu'un contrôle limité
sur le code généré, malgré l'existence de
centaines d'options de compilation : il manque toujours
celle dont on a besoin.
Non seulement les compilateurs actuels ne permettent aucun contrôle du code à l'instruction près, mais
il ne savent pas encore gérer automatiquement les instructions MMX ou SSE qui sont nécessaires pour accélérer
les calculs avec les algorithmes multispin. L'utilisation d'un compilateur pour du code "final"
est donc un effort superflu, car il ajoute un niveau d'abstraction parasite dans l'analyse du problème.
Les espoirs de générations automatique de codes
"preque parfaits" se sont évanouis devant l'ampleur du manque de réelle intelligence des outils.
Ecrire le coeur du calcul à la main, à l'aide d'un simple outil disponible gratuitement sous GPL,
s'est révélé finalement beaucoup plus efficace et plus facile que de forcer les compilateurs à créer
du code qu'ils ne peuvent pas générer. De plus, cela a nécessité un important effort au niveau
de la théorie derrière les calculs de collision, qui a permis la création d'une nouvelle formule.
Le code actuel a atteint un point critique qui nécessite de nombreux efforts pour le dépasser.
Dans l'état actuel du projet, il est alors rentable de se concentrer sur les outils de codage "assisté",
dans lesquels les techniques de codage développées pour ce projet peuvent être réinvesties.
Le projet "GNL" permettra de recoder entièrement le source du projet, de le porter vers d'autres
architectures, tout en permettant d'atteindre et de se maintenir à la puissance de crête de
la plateforme cible. Si cet outil interactif avait existé au début du projet, le programme
serait fonctionnel plus rapidement et plus facilement. Beaucoup de "travail sur papier", d'efforts
et de temps aurait été économisé. Toutefois, le "travail sur papier"effectué
pour ce projet a permis de mettre au point et tester en grandeur réelle des techniques à la base
de GNL (allocation des registres, évaluation des accès à la mémoire etc).
1.6 : Une nouvelle formule :
L'une des découvertes les plus inattendues de ce projet est l'équation booléenne au coeur du calcul des
collisions. C'est aussi un point très important du mémoire car il découle d'une analyse plus aprofondie
et sous un autre angle que la formule (classique aujourd'hui) donnée
au chapitre IV.7.
La nouvelle formule essaie de correspondre aux exigences du Pentium : peu de registres,
bande passante réduite, pairage des instructions compliqué... alors que la formule classique
nécessite de nombreux termes temporaires dans le graphe de dépendences, favorisant les
architectures RISC avec de très nombreux registres. En comparaison, la nouvelle formule
peut être utilisée sur des calculateurs vectoriels (par exemple CRAY classiques avec 8 registres vectoriels).
La nouvelle formule ne remplace pas l'ancienne, nous pouvons remarquer qu'elle la complémente
et élargit le domaine d'application et d'utilisation du modèle FHP saturé. En
l'absence d'analyse booléenne plus poussée, il est difficile et peut-être inefficace d'utiliser
la formule de d'Humières si moins de 32 registres sont disponibles pour les données (c'est à
dire que les pointeurs, compteurs de boucles etc. doivent être séparés ou très peu nombreux).
Au contraire, si le rapport mémoire/calcul d'une machine particulière
efface le problème des variables temporaires
d'une manière ou d'une autre, la formule de d'Humières est plus efficace car le nombre
total d'opérations booléennes est inférieur à la nouvelle formule.
Il reste encore à prouver que la vielle formule est optimale, ce qui est une tache difficile
en raison de la spécialisation de chaque cas : quelles opérations booléennes sont admises ?
XOR, ANDN, NAND, ORN ? La formule peut changer complétement en ajoutant ou en supprimant un
opérateur et la pratique montre que les compilateurs VHDL sont incapables de répondre à cette
question de manière satisfaisante. L'analyse brute est inefficace, il faudrait donc trouver
une nouvelle méthode pour "casser" ce type de formule lourde en instructions simples.
Loin d'avoir résolu le problème, ce travail relance la question épineuse de l'efficacité des
calculs. Il apporte un nouvel élément (une autre formule) ainsi qu'une nouvelle manière
d'appréhender la question des collision saturées. Le long travail qui leur a permis de voir le
jour n'aurait pas été nécessaire si les microprocesseurs courants avaient plus de bande passante
vers la mémoire, plus de registres, et des outils plus efficaces pour "casser" le graphe
de dépendances de données de manière satisfaisante.
Cependant, la formule de d'Humières
ressemble un peu à l'algorithme de Bresenham dans le sens où avant son existence, le problème
était considéré comme "difficile" (peu de personnes avaient envie de transformer le modèle
en code informatique, en raison de sa complexité qui intéressait peu les physiciens). Lorsque le
code a été publié, il a été réutilisé abondament et le problème n'a pas ressurgi car le code
était estimé "satisfaisant" (quand il était correct...).
Aujourd'hui, comme l'algorithme de Bresenham, la formule "canonique" ne satisfait plus
les contraintes complexes imposées par certaines classes de machines. Espérons que d'autres
personnes continueront les travaux dans ce domaine après ce mémoire.
1.7 : Intégration complète de l'algorithme de visualisation dans celui du calcul :
Tout comme pour le strip mining, intégrer les calculs de visualisation dans la boucle de calcul
permet de bénéficier des propriétés de localité spatio-temporelles des
modèles FHP et similaires. Les microprocesseurs comme le Pentium, limités en bande passante
vers la mémoire externe, bénéficient de ce type de programme car ils
évitent ainsi de saturer inutilement le bus externe par des
cache miss à répétition. L'intégration des différents algorithmes, lorsqu'ils portent
sur une même donnée, permet de rééquilibrer les caractères memory bound et
CPU bound et d'entrelacer la latence des mémoires avec les lourds calculs.
Les coeurs OOO (comme le PII ou l'Alpha 21264) ont principalement été conçus dans cette
optique, l'exécution spéculative de dizaines d'instructions permet de continuer
le programme en attendant une donnée venant de la mémoire centrale.
Lors de la conception d'un programme de calcul intensif, il est donc important de bien
faire cohabiter la partie de calcul brut et les parties qui ne participent pas au calcul
proprement dit : bien que le résultat ne change pas, il devient inutile s'il n'est pas
présenté correctement à l'utilisateur. Le problème se complique avec l'introduction
du strip mining, mais heureusement il se résoud naturellement dans notre cas précis,
ce qui peut ne pas être vrai pour d'autres cas.
Le travail n'a pas abordé la collecte de statistiques, se limitant à la mesure de
la densité en particules, mais la remarque reste valable : il faut autant que possible
réunir toutes les parties du code autour des mêmes données, afin de bénéficier des mémoires caches
de données. Le code exécutable tient souvent largement dans la cache des instructions,
la taille du code n'est pas actuellement un problème.
1.8 : Mesurer son code :
C'est un détail qui est tout le temps oublié, mais même sans le langage assembleur, même si peu de moyens
sont disponibles, il est toujours important de connaitre à tout moment le temps d'exécution
de chaque bloc d'instructions. Il faut toujours "profiler" son code et comparer ses performances entre
chaque modifications.
Tous les détails qui rendent ces éléments cohérents sont très importants, car comme
noté précédemment, l'ajout d'un détail peut remettre en cause le programme entier.
La plus grande prudence est donc conseillée. Un de mes mots d'ordres est "coder proprement
paie toujours" (proprement dans le sens de l'efficacité) car la mentalité actuelle dans le milieu
informatique est que "les ordinateurs sont bien assez rapides comme ça, pourquoi se compliquer la tâche ?".
Cela conduit à des situations où des programmes tournent à 10% de la puissance nominale de l'ordinateur,
sans que personne ne s'inquiète. Or selon le cas et avec du logiciel optimisé, on pourrait économiser
90% du prix d'achat sur le matériel, à performance égale. Cela semble inaproprié pour les calculs de
ce mémoire, mais devient très important pour un serveur central ou institutionnel coûtant des millions de francs.
2 : Conclusions des expériences
2.1 : FHP-3 est memory bound et CPU bound sur x86 :
Les mesures ont montré que l'on ne peut plus améliorer radicalement les performances de FHP-3,
on se heurte toujours à une partie qui dépend trop des calculs ou de la mémoire. Le cas
du x86 est dramatique car ni la mémoire ni les instructions ne sont conçues pour supporter et maintenir
leur puissance théorique. Le cadre des applications bureautiques et ludiques, permettant
l'expansion du marché de masse des particuliers, ne justifie pas une refonte ou un abandon
de la vieille architecture du x86, même si Intel essaie de promouvoir l'IA64
pour les domaines où la recompilation est déjà une nécessité.
L'IA64 réunit probablement le
pire du VLIW et du SPARC en essayant de faire mieux que le x86 : nous ne sommes pas
prêts de voir une architecture "sympatique" pour FHP dans le commerce avant longtemps.
2.2 : Il est possible de descendre à 3 cycles par octets :
Malgré une substancielle augmentation de la taille du kernel de calcul, par rapport
au code multisite 32 bits étudié dans le passé, il est possible d'aller encore plus vite
et d'être plus flexible grâce au code multispin entrelacé. Il est peu probable que l'on puisse
descendre beaucoup plus bas, par exemple 1 cycle par cellule, car la mémoire freine le
processeur de plus en plus si de très longs mots (128 bits ou plus) sont utilisés.
De nombreuses améliorations peuvent toutefois êtres effectuées et ne manqueront pas
de voir le jour. Les codes multisites sont donc bien morts.
2.3 : A condition d'effectuer de nombreux efforts, il est possible d'utiliser
des PC pour des calculs lourds :
Comme ce mémoire le prouve, il est possible de compter sur le rapport performance/prix/disponibilité
intéressant du PC si de nombreux points sont pris en compte et traités :
- il faut pouvoir remettre en question de nombreux points acquis : algorithmes,
structures de données, techniques de développement...
- il est de plus en plus difficile de contrôler TOUS les aspects du calcul car
les architectures logicielles et matérielles sont de plus en plus complexes
- le résultat sera souvent proportionnel à l'effort, il faur donc pouvoir
accorder beaucoup de temps et user sa patience sur des problèmes parfois incompréhensibles
Les PC sont souvent utilisés de nos jours pour des tâches réservées hier à des ordinateurs immenses
et chers. La croissance des PC, si on regarde les premières générations, est disproportionnée
(bande passante mémoire, parallélisme, ILP) et correspond à des besoins de rentabilité sur le marché
de masse pour des individus, mais pas à des applications scientifiques.
2.4 : Un PC équivaut presque à une CAM8 :
Les mesures effectuées au MIT en janvier 2000 montrent que les PC de bureau de dernière génération
sont presque aussi rapides qu'un bloc CAM8 (8 cartes à 25MHz). Les tout derniers microprocesseurs généralistes
permettent de rivaliser avec des ASIC créés il y a plusieurs années. En terme de génération équivalente, si
l'on considère la règle de Moore, l'optimisation poussée du code a permis probablement de gagner trois ou
quatre années par rapport à un code non optimisé. Le code est 4 fois plus rapide que le plus rapide des
codes testés, ce qui permet d'affirmer que l'effort a permis de gagner 3 ans. Ce gain permet d'utiliser
une machine plus vieille à vitesse égale (donc moins chère) ou bien de gagner 3 ans sur la machine la plus récente.
Cet aspect d'économie est valable si le code original était "bâclé", mais reste dans le cadre de la démonstration
du fait qu'un codage consciencieux n'est pas une perte de temps à longue échéance.
2.5 : La loi de Moore est trompeuse :
La règle de Moore, découverte par le co-fondateur d'Intel dans les années 70, ne signifie que ce qu'elle
dit : que le nombre de transistors est multiplié approximativement par quatre tous les trois ans.
Il est donc abusif de considérer qu'un programme fonctionnera quatre fois plus vite dans quatre ans.
Les grands constructeurs préparent de nouveaux coeurs de plus en plus étranges et de moins en moins
adaptés aux algorithmes actuels. Les détails
architecturaux deviennent de plus en plus complexes et il est de plus en plus difficile de tous les prendre
en compte lors de la conception d'un programme. Cela veut aussi dire en filigrane que pour tourner quatre fois
plus vite dans quatre ans, il faudra complétement reprendre la conception du programme à partir de zéro.
Les efforts à fournir afin d'accélérer un programme deviennent de plus en plus grands, à
la mesure des efforts fournis pour augmenter le nombre de transistors sur les puces.
Les compilateurs ne seront plus assez sophistiqués et il faut d'autres moyens pour programmer.
Enfin, comme de nombreux exemples le prouvent, l'histoire des ordinateurs ne suit pas une courbe
monotone sur du papier à échelle semi-logarithmique : de nombreuses révolutions
nous attendent et personne ne pourra plus utiliser ses sources en C écrits il y a dix ans.
Si l'avenir de l'informatique est garanti pour les vingt prochaines années, les chemins empruntés
sont inconnus et il faut se préparer maintenant à la concrétisation de projets incroyables aujourd'hui.
2.6 : Le sujet des gaz sur réseaux booléens est loin d'être tari :
Alors que les études actuelles portent sur des modèles à virgule flottante sur des approximations
de Bolzmann, la présente étude du modèle FHP est loin d'épuiser toutes les ficelles des informaticiens
et des physiciens. FHP reste un "terrain de jeux" incontournable pour comprendre de nombreux problèmes
et phénomènes de mécanique des fluides, de mécanique statistique, d'algorithmique, il est donc important
de continuer les études dans ce domaine, non pour faire de FHP un outil, mais comme modèle à part entière,
pour être étudié et approfondi (le manque d'études dans ce domaine étant le plus souvent dû à un manque de
connaissance du sujet, décourageant les étudiants). Un autre piège est la simplicité apparente du modèle,
qui séduit les débutants mais qui les perd ensuite. Il est certain que d'autres approches sont nécessaires.
3 : Sujets des recherches futures
Le programme, même s'il fonctionne, nécessite de nombreuses améliorations plus ou moins complexes, décrites ici :
3.1 : Mesurer la pression :
Le problème "annexe" le plus important, celui de la mesure de la densité en particules (donc de la pression), a
été résolu dans ce mémoire (popcount parallèle réutilisé dans la phase de détection, puis addition semi-parallèle).
Pourtant, un aspect intéressant des mesures en soufflerie n'est pas la mesure dans le fluide, mais sur les
parois. Il faut donc mettre en place un dispositif "comptant les bits" qui sont réfléchies par une paroi.
Cela peut nécessiter une simple "adaptation" des algorithmes des listes de modification, ou un nouveau type
d'algorithme, mais le sujet est sérieux : il permettra d'implémenter un jour des "intéractions fluide/solide",
comme la mise en mouvement d'un objet dur par le fluide qui l'entoure (balle dans un courant d'air, vibration
d'une surface en fonction de turbulences...). C'est un domaine où les LGA n'ont pas été appliqués, malgré les
potentiels certains de ce modèle. L'objection de Norman
Margolus à propose des parois mobiles concerne la non-réversibilité
du mécanisme, ce qui ne nous intéresse pas dans le cas des écoulements dissipatifs.
3.2 : Emission de particules :
Le présent programme manque cruellement d'un "générateur de particules" associé à son contraire ("avaleur" ?).
Le problème est caractéristique des veines de soufleries : il faut créer un vent uniforme, qui puisse imposer une
vitesse contrôlable du fluide. Il faut donc "créer" et "supprimer" des particules à certains endroits, à une
vitesse particulière, tout en conservant la pression totale (le
nombre de particules dans la veine, voir la partie III).
Il n'y a pas de problème conceptuel notable, mais il faut tout de même le programmer. En attendant, l'utilisateur
est obligé d'utiliser un nombre fixe de particules qu'il doit programmer en assembleur : des efforts de
programmation subtanciels et nombreux sont encore à fournir. De plus, il faudrait mettre au point un algorithme
de mesure du "vent" afin de rétrocontrôler ce mécanisme.
3.3 : Multi-CPU :
Le "stub" de bi-processing symétrique a été écrit mais n'est pas utilisé car le reste de l'algorithme n'est
pas terminé. Quand ce sera le cas, il faudra adapter légèrement le code (principalement : copier/coller/renommer)
puis enlever le code en commentaire (en faisant attention aux bugs qui ont déjà été trouvés).
Le véritable problème est dans le cadre d'un beowulf car de nombreux autres problèmes devront être résolus.
Les prochaines années verront probablement apparaitre des codes d'exemples. Le programme devient encore plus
compliqué lorsque l'espace d'adressage n'est plus partagé.
3.4 : Extension du code et du modèle :
Le code développé ici est un modèle simple mais suffisament représentatif des problèmes à résoudre
dans des cas réels, même avec des modèles différents. Il peut donc être adapté à des modèles "thermiques"
(plusieurs vitesses de particules), multiphases (plusieurs "couleurs" de particules), compressibles, avec
des géométries différentes (D2Q9 ou autres) et avec plus ou moins de particules immobiles (pour résoudre
le problème de l'invariance galliléenne). Un gros effort de codage devra être effectué pour chaque cas.
Cependant, cet effort est d'abord de l'ordre informatique, il faut donc que le recodage du projet tienne compte
des besoins d'adaptation du programme pour anticiper la
résolution des problèmes futurs. Le code actuel, étude de
cas pour un sujet particulier, devra encore beaucoup mûrir pour devenir une plateforme d'expérimentation
encore plus générale.
3.5 : Langage script :
La définition et la programmation d'un langage script universel permettra l'automatisation des mesures et
la description des objets à l'intérieur du domaine
d'étude. Actuellement, la définition de la géométrie des objets est
inclue dans le source en assembleur, ce qui impose un réassemblage à chaque changement de géométrie.
Les opérations interactives (changement de taille du tunnel, pas à pas...) ne sont pas absolument précis
et nécessite de programmer des mécanismes pour contrôler plus finement tous les paramètres.
Un format de fichiers et des mots-clés sont actuellement en stade de réflexion mais leur implémentation
nécessite un effort trop important pour être effectué actuellement : il faut que d'autres problèmes plus
importants soient résolus (tout d'abord l'exactitude des collisions).
3.6 : Evolution de la plateforme :
Les nouvelles instructions "SSE" introduites dans le Pentium III permettent d'envisager un doublement
de la performance brute du programme (à fréquence d'horloge égale) avec peu de changements notables
du code. Il faudrait tenir compte des tailles doublées des registres (128 bits au lieu de 64), de la configuration
des MTRR et des instructions de gestion de la mémoire et des flux. Ces travaux sont déjà possibles mais
seront encore plus faciles lorsque tout sera recodé avec GNL, et quand la plateforme (PIII)
sera plus largement répandue (et moins chère). C'est donc une échéance de 1 à 2 ans.
4 : Applications
Avec des adaptations plus ou moins profodes, le programme FHP peut être utilisé dans de nombreux domaines :
4.1 : Acoustique :
Déjà utilisés dans ce domaine, les modèles de gaz sur réseaux (FHP, Bolzmann) ne sont pas encore très répandus
malgré leur fort potentiel. Cela peut être résumé comme un problème d'"école", les chercheurs en acoustique
étudiant les équations (directes) d'acoustique et non de mécanique statistique.
Les LGA sont très bien adaptés pour visualiser les ondes sonores et permettent des géométries arbitrairement
complexes : elles surpassent les méthodes spectrales pour les cas non triviaux. Par exemple, ils sont
utilisés pour étudier les turbulences autour des voitures, et donc déterminer et améliorer leur niveau
de bruit aérodynamique (leur silence).
Les LGA peuvent permettre aussi d'effectuer des simulations d'instruments de musique. En l'absence d'interactions
fluide/solide, les anche simples, doubles et lipales ne peuvent pas être simulées. Il reste cependant
les vibrateurs de type "flûte" (à biseau) qui peuvent être étudiés en attendant de meilleurs programmes.
Ainsi, il sera possible d'étudier un instrument (pour l'instant en 2D) avec un PC suffisamment rapide,
et de générer un son de flûte véritablement réaliste, sans utiliser la moindre méthode de reproduction
classique (analyse spectrale, analyser d'impédance du corps résonant, échantillonnage). Les applications
en musique et en synthèse directe sont alléchantes. Le niveau de bruit des LGA booléens comme
FHP est toutefois trop important pour ce type d'applications, les modèles en virgule flottante sont donc de rigueur pour
ce type de problèmes.
4.2 : Cryptographie :
Les LGA de type FHP ont des propriétés macroscopiques très intrigantes : contrairement àla majorité des Automates
Cellulaires classiques, ils ont la capacité de "décorréler" un état initial et de le transformer en
bruit "brownien" de manière fondamentalement non-linéaire. Le nombre de pas de temps dépend des propriétés
du "signal" initial (configuration
initiale des particules). Les gaz sur réseaux booléens sont donc très intéressants dans le domaine de
la cryptographie, car ils sont potentiellement réversibles, ils sont peu compliqués à calculer,
leur état initial est très difficile à retrouver en l'absence des paramètres du calcul et
les possibilités d'utilisation sont très nombreuses. Ils peuvent être utilisés comme générateurs de
nombres aléatoires ou comme "bruiteurs", avant ou après le calcul. Le brevet des cryptographie par automates
cellulaires réversibles ne s'applique pas directement et le MIT travaille sur le sujet. L'efficacité pratique
de cette technique reste à démontrer mais elle dépend principalement d'une utilisation judicieuse des LGA,
donc l'efficacité potentielle se situe probablement entre DES et RSA. Même si ce n'est probablement pas
une révolution pour la cryptographie, c'est un élément important parmi l'arsenal des techniques déjà
disponible (courbes elliptiques, nombres premiers, transposition, substitution, permutation...) avec lequel
il faudra dorénavant compter. Dans ce cadre, la vitesse de calcul est un élément absolument critique.
Il faut toutefois rester très prudent dans ce domaine car aucun exemple n'a encore été cryptanalysé. Malgré leurs
caractéristiques non linéaires, leurs propriétés sont étudiées depuis longtemps et ils disposent toujours d'une
entropie caractéristique qui permet une attaque par les équations de Bolzmann.
4.3 : Réalité Virtuelle / jeux vidéo :
L'accélération de l'algorithme permet d'envisager la
simulation des phénomènes turbulents en "temps réel"
ou même plus vite, ce qui est toutefois très subjectif selon
le cas. Pour les jeux vidéo, où l'exactitude des calculs et la réalité scientifique des résultats importent
peu, les gaz sur réseaux offrent une opportunité incomparable pour les mondes simulés. Les techniques
courament utilisées sont des simplifications peu rigoureuses et parfois irréalistes (vent dans l'herbe,
nuages de "plasma"...). Avec la montée en puissance des consoles de jeu vidéo, l'utilisation de LGA
n'est plus qu'une formalité actuellement et pour le futur. Non seulement des phénomènes réalistes peuvent
être visualisés, mais en plus les éléments (acteurs, objets) du jeu peuvent intéragir avec le phénomène.
Actuellement, aucune application n'est envisagée dans ce domaine. Espérons que ce n'est qu'une "frilosité
passagère" : l'effet de mode peut favoriser une utilisation et un développement très actifs dans ce domaine.
Il "suffit" juste de lancer correctement l'idée.
4.4 : Education :
La simulation interactive de phénomènes de mécanique des fluides peut être aussi d'intérêt éducatif.
En classes de physique et chimie, la disponibilité d'un "fluide virtuel" non nocif et parfaitement
contrôlable peut diminuer les risques de certaines expériences et permet donc aux élèves de manipuler
eux-mêmes les produits. En classe de Technologie Industrielle, cela permet aussi de simuler des vérins
hydrauliques ou des pompes avec un matériel moins encombrant, afin de tester des algorithmes de contrôle
de montée en charge de pompe ou de régulation par exemple.
4.5 : Industrie :
L'industrie commence timidement à adopter les gaz sur réseaux dans quelques domaines, pour des applications
pratiques plus ou moins attendues. Le calcul "industriel" pour les carrosseries et les tuyauteries permet
à la société EXA de s'imposer progressivement. De nombreux domaines sont encore en attente d'un miracle
que les LGA peuvent produire dans la chimie (réactions d'advection/diffusion), le pétrole (stockage et
infiltration dans les sables), la climatisation (où placer la bouche d'aération dans une pièce sans
déranger les usagers ?), les peintures (viscosité et écoulements), les risques
industriels (souffles d'explosions et écarts entre bâtiments), l'urbanisme (advection des gaz d'échappement),
la propagation des flammes et de nombreux problèmes de tous les jours qui ne sont pas encore résolus
de manière définitive par les méthodes classiques.
4.6 : Derniers mots sur les applications des LGA :
Aujourd'hui, les LGA ont fait l'objet de recherches scientifiques poussées dans des domaines où
ils apportent un réel avantage par rapport à la dynamique moléculaire,
aux techniques spectrales et aux équations classiques : le facteur déterminant est l'indépendance
totale entre la complexité du calcul et la complexité des géométries étudiées.
Le premier domaine d'adoption concerne les fluides multiphases et la séparation des phases, la tension
de surface, les fluides immiscibles, les interfaces solide/liquide/gaz. Ce domaine reste proche de la mécanique
statistique. L'image suivante représente une séparation de phase calculée par Rothman et Keller :

|
Un autre domaine qui bénéficie des avantages de LGA est l'infiltration et le mouillage en milieu poreux.
Nous voyons sur l'image ci-contre l'infiltration de pétrole (hydrophobe, orange, opaque)
remplaçant de l'eau (bleue) dans un grain de sable de Fontainebleau,
calculée en 3D par John Olson |

|
Les LGA se sont montrés inadaptés pour les calculs aéronautiques à cause de la faible vitesse permise
(< Mach 0,3) et du faible nombre de Reynolds. La simulation des allées de Von Karman est facile, comme nous avons pu
le voir, mais l'explosion quadratique du temps de calcul rend les gaz sur réseaux classiques inadaptés pour des
nombres de Reynolds supérieurs à 10000. L'exemple d'EXA montre que des ordinateurs massivement parallèles
sont utilisés avec des temps de calcul similaires par les autres techniques. Les seuls avantages sont la
plus gande finesse, la résolution dans le domaine temporel et la meilleure fiabilité des résultat, le temps
de calcul n'est plus un critère déterminant.
5 : Limites du projet
Le modèle FHP3 a été plus difficile à implémenter que prévu, sa programmation nécessite des moyens sophistiquée
et des connaissances solides qui sont très diffuses dans la bilbiographie classique. La technique prévue
au départ pour l'équation booléenne n'a pas fonctionné (compilation VHDL puis GCC puis NASM) pour des raisons
d'efficacité. Le travail a dû être effectué entièrement à la main, une nouvelle équation a été déduite à
partir de zéro : cela a consommé la moitié du temps du projet qui s'est étalé sur deux ans. Le manque d'outils
logiciels adaptés a aussi ralenti la progression.
Dans ces conditions, l'ambition initiale de "clore le sujet" n'a pu être atteinte, au contraire : ce travail
a levé une grande quantité de questions de toutes sortes. Quelques-une ont été résolues mais la plupart
est hors du domaine d'étude initial, elles sont plus théoriques ou trop complexes.
La limite du projet est surtout au niveau du temps d'étude car le sujet est inimaginablement vaste et peu de
personnes travaillent actuellement dans ce domaine. L'autre limite, pratique, est très importante car le "budget"
(matériel, financier) est quasiment inexistant (ce fut déjà une chance de disposer d'une plateforme biprocesseur).
Enfin, les logiciels sont actuellement inadaptés à la tâche de programmation efficace en langage machine :
beaucoup de temps a été investi dans le développement de techniques de programmation.
6 : Et maintenant ?
La première chose à faire est d'améliorer l'environnement de développement. Le projet GNL est l'aboutissement
d'années de réflexion sur la pratique du codage en assembleur sur machines superscalaires. Les premiers fichiers
sont écrits (l'interface et l'importation de fichiers C sont commencés) pour l'environnement Unix (le logiciel
GNL est complétement portable). Il faut concevoir des API afin que de nombreux modules d'assistance au codage
puissent communiquer avec l'utilisateur. Des modules d'entrée et de sortie doivent aussi être conçus pour chaque
langage et chaque processeur supporté.
Une fois qu'une version suffisamment complète de GNL sera prête, le programme de gaz sur réseaux de ce mémoire
sera recodé, analysé, amélioré, porté et pourra accueillir les suggestions du début de ce chapitre. GNL ne
se limite pas à ce projet de LGA, le but avoué est de remplacer une grande partie du codage textuel classique.
Si on peut recoder entièrement le programme avec GNL et l'améliorer facilement, ce sera une sorte de première
mise à l'épreuve du concept et permettra de l'appliquer à d'autres domaines sensibles : programmation
de kernels de systèmes d'exploitations, de routines d'interruptions, de kernels de calculs, de moteurs d'IA
ou de 3D pour les jeux vidéos, et même pourquoi pas pour le prototypage rapide d'algorithmes.
Enfin, à mesure que les processeurs superscalaires exécutent de plus en plus d'instructions en parallèle pour
chaque cycle, il devient de plus en plus difficile de programmer des compilateurs pouvant extraire l'ILP
d'un programme écrit en C. Les moyennes actuelles sont de l'ordre de trois instructions par cycle
dans des conditions "idéales", ce qui est à la fois insuffisant pour augmenter substanciellement
la performance des processeurs et trop compliqué pour les compilateurs. GNL expose le parallélisme d'un
programme à de nombreux niveaux et permet donc de mieux profiter des processeurs futurs. GNL sera ainsi capable
d'aider à l'adaptation du programme vers le Pentium II (les règles de pairage sont différentes).
Pour ce qui est des applications pratiques, le modèle FHP n'est pas aussi efficace pour des simulations
à grands nombres de Reynolds. Je vais donc essayer d'appliquer mes connaissances et mes techniques dans le
domaine des gaz sur réseaux non booléens comme le modèle Lattice Bolzmann ou BGK. Une voie de recherche
à explorer est l'utilisation du modèle ILG (Integer Lattice Gas, sorte de compromis entre Bolzmann et FHP)
avec un système de numération logarithmique (nombres entiers différent de Base-2, plus simples
que les nombres en virgule flottante). La parallélisation de ce travail permettrait de simuler de larges
systèmes efficacement, c'est l'objet du projet beo-kragen (beowulf de Kragen Sitaker).
Ressources bibliographiques
Si une thèse peut être consultée à Jussieu, sa référence est fournie.
| [1] |
Bernard Ourghanlian "Les microprocesseurs Alpha" InterEditions, 1995,
ISBN 2 7296 0565 7
Excellente introduction à ce processeur révolutionnaire, écrite en français par
le directeur de développement de Digital. Ce n'est pas une documentation technique
pure, car elle explique aussi le pourquoi du comment de chaque aspect et
de chaque décision de la conception du modèle de programmation. Bon livre
sur l'architecture RISC du futur.
|
| [2] |
Henri Lilen - René-Véran Honorat "Microprocesseurs PowerPC" ed. Dunod,
1995, ISBN 2 10 002464 7
Ecrit en francais, ce livre présente le modèle de programmation de la famille PowerPC
et s'attarde sur les membres commercialisés avant la sortie du livre. Plusieurs
techniques architecturales sont expliquées comme l'exécution dans le désordre, mais
la suite est plutôt une traduction des documents anglais. On comprend donc le PPC
sans vraiment en savoir plus...
|
| [3] |
David A Patterson - John L Hennessy "Computer Organisation & Design:
the hardware/software interface", Morgan Kaufmann, 1994, ISBN 1 55860 282 8
C'est LE "Patterson & Hennessy", qui explique clairement les fondements de l'architecture
des presque tous les ordinateurs. Il raconte leurs aléas et leurs avancées et
permet de mieux comprendre l'importance de la relation entre le logiciel et le
matériel qui le fait tourner, en fonction de leur rapport performance/prix.
Il ne faut pas confondre ce livre avec leur précédent ouvrage "A quantitative
approach" (le "QA") qui le précède.
|
| [4] |
Gilles Deghilage "Architectures et programmation parallèles", Addison-Wesley,
1992, ISBN 2087908 023 1
"Approche pratique en environnement scientifique sur multiprocesseurs Silicon Graphics",
ou comment tirer le meilleur de architectures MIMD, des compilateurs, des algorithmes...
Les aspects théoriques et pratiques sont abordés et les résultats sont comparés
aux autres plateformes existantes. Il introduit dans leur contexte les techniques
de parallélisation de code comme le strip mining.
|
| [5] |
Hans-Peter Messmer "Pentium et compagnie", Addison-Wesley, 1994, ISBN 2 87908 074 6
Bien qu'entaché de quelques erreurs et plein de détails inutiles,
l'intérêt de ce gros livre est de présenter sous toutes ses coutures le monstre
CISC de 3 millions de transistors, ainsi que ses relations avec ses voisins directs:
contrôleur de cache, de mémoire, de bus PCI... Cette synthèse met le doigt sur énormément
d'aspects, électroniques, architecturaux ou de programmation, qui sont nécessaires
pour développer efficacement, mais il vaut mieux se référer aux constructeurs et aux
sites x86.org et PCguide.com pour avoir une information plus fiable.
|
| [6] |
Alfred Aho - Ravi Sethi - Jeffrey Ullman et al. "Compilateurs : principes, techniques
et outils", InterEditions, 1989, ISBN 2 7296 0295 X
Le "dragon book", c'est la raison pour laquelle je n'utilise pas de compilateur. C'est aussi
la raison pour laquelle j'en utilise un. Seulement, je sais maintenant quand je peux m'y fier.
Accessoirement, permettrait de faire un compilateur optimiseur pour le PII en MMX si cela
en valait la peine...
|
| [7] |
Michael Abrash "Le Zen de l'optimisation du code", Sybex, ISBN 2-7361-2128-7
Devrait être lu par toute personne considérant coder "correctement", bien que l'aspect
"assembleur" puisse repousser les habitués du "tout C". Quand on va à la chasse à la
performance, "on ne fait pas d'omelette sans casser d'oeufs", et l'auteur nous apprend
à faire enfin fonctionner le merveilleux compilateur qui est entre nos deux oreilles.
En plus, ce livre est facile à lire.
|
| [8] |
Ronald J. Tocci "Circuits Numériques : théorie et applications", Dunod, 1992, ISBN 2-10-001576-1
Présente entre autres les techniques de base de simplification manuelle d'équations booléennes.
Malheureusement insuffisant avec plus de 5 ou 6 variables d'entrée et plus d'une variable en sortie.
De plus, l'analyse se réduit aux sommes de produits alors qu'on dispose souvent du XOR.
|
| [9] |
Daniel H. Rothman et Stéphane Zaleski "Lattice-gas cellular automata",
Collection Aléa Saclay, Cambridge University Press, 1997, ISBN 0-521-55201-X
Sous-titré "Simple models of complex hydrodynamics", ce livre anglais de physique statistique
est écrit par deux spécialistes et fournit des bases importantes sur la théorie des gaz
sur réseaux. Après un exposé complet, les domaines de recherche des auteurs transparaissent
dans l'étude des infiltrations des milieux poreux et de la transition de phase. Niveau doctorat.
|
| [10] |
Valérie Guimet "Analyse numérique et simulation de problèmes d'interaction
fluide-structure en régime incompressible", thèse soutenue le 20 octobre 1998
Cette thèse pour le doctorat de Mathématiques Appliquées de l'université Paris VI
explique des méthodes classiques de simulation de couplage entre des objets déformables
(en 1D et 2D) et des fluides turbulents (en 2D et 3D). Bien que le domaine du calcul
intensif soit abordé (ressources informatiques de l'ONERA), aucune explication pratique
n'est donnée.
|
| [11] |
Jean-Pierre Rivet "Hydrodynamique par la méthode des gaz sur réseaux", thèse #88NICE4215
en Mécanique fondamentale et appliquée
Dirigée par Uriel Frisch, cette thèse communique une grande somme de connaissances théoriques
(par l'explication des modèles) et pratiques (par l'explication des algorithmes) sur
les gaz sur réseaux bi et tridimensionnels. Le RAP-1 est décrit mais surtout
des simulations tridimensionnelles sur CRAY-2 sont effectuées et expliquées.
Pas de code source pourtant mais un intérêt certain pour l'efficacité.
|
| [12] |
Pierre Audibert "Méthodes de grille pour le traitement des problèmes de mécanique des
fluides", mémoire de maitrise de l'université Paris 8
Cet exposé présente clairement 3 méthodes différentes avec explications et programmes
sources commentés. Bien que le modèle FHP soit utilisé en dehors de ses limites, le mémoire
montre clairement les avantages et inconvénients pratiques et théoriques de chaque approche
(les équations différentielles classiques et la méthode des tourbillons sont aussi présentées).
L'efficacité est implicitement limitée par la plateforme (compatible PC sous MS-DOS, programmé
en Turbo C).
|
| [13] |
Yue Hong Qian "Gaz sur réseaux et théorie cinétique sur réseaux appliquée à l'équation de
Navier-Stockes", thèse #90PA06 658 de mécanique et physique statistique
Dirigée par D. d'Humières et P. Lallemand, cette thèse commence par l'étude spectrale
d'un gaz sur réseau unidimensionnel pour extrapoler vers 2 dimensions (FHP, D2Q9 etc)
puis 3 dimensions (FCHC et similaires). L'intérêt est principalement de consolider
et d'explorer les travaux théoriques effectués 5 ans plus tôt.
|
| [14] |
Umberto d'Ortona "Hydrodynamique et Gaz sur réseau", thèse
Explication claire, malgré quelques détails ambigus, des gaz sur réseau classiques dans les
premiers chapitres. Les néophytes aprécieront de pouvoir comprendre certains détails
et les solutions apportées. La thèse étudie entre autres les phénomènes de capillarité
(interfaces entre une goutte d'eau et un autre fluide).
|
| [15] |
Valérie Pot "Etude Microscopique du transport et du changement de phase en milieu
poreux par la méthode des gaz sur réseaux", thèse #94PA06 233
Ces travaux font l'objet d'un chapitre entier dans le livre de Stéphane Zaleski.
Beaucoup de formules et pas de code.
|
| [16] |
Stéphane Zaleski "Les transitions de phase calculées", Pour la science #183, janvier 1993
Article de présentation (2 pages) annonçant les résultats encourageants de recherches
sur la transition de phase en 3D, améliorant les techniques présentées par Jean-Pierre Rivet
et pour des règles d'interaction non locales.
|
| [17] |
Bernard Derrida "Dynamique d'un gaz sur réseau", Pour la science #184, février 1993
Cette "récréation informatique" présente un algorithme 2D pour simuler l'évaporation ou
la condensation d'une goutte d'eau. Rien de commun avec FHP mais il simule une transition
de phase (liquide/gaz) sans utiliser les intéractions non locales utilisées par Zaleski,
ce qui fait de cet automate cellulaire une alternative intéressante.
|
| [18] |
Pierre Lallemand "Les gaz sur réseau : un nouveau médium pour le calcul des écoulements",
Revue du Palais de la Découverte, avril 1987, vol. 15, numéro 147
C'est cet article qui m'a fait découvrir le domaine des LGA. La théorie y est exposée
ludiquement et le modèle FHPII est succintement expliqué, suggestivement mais sans aider
pour la programmation pratique. En particulier les règles de collisions sont expliquées
mais la mise en pratique n'est pas évidente (création de la table des collision).
|
| [19] |
U. Frisch, B. Hasslacher, Y. Pomeau "Lattice gas automata for the Navier-Stockes
equation", Physical Review Letters, 7 avril 1986, vol.56, pp 1505-1508.
C'est l'article de référence cité par tout papier ou document portant sur les gaz sur réseaux.
Appelé dans cet article "HLG" pour "Hexagonal Lattice Gas", le modèle présenté retiendra
les initiales des auteurs pour la postérité. Le passage du modèle HPP (carré) au
voisinage hexagonal est expliqué, trois règles de collisions sont introduites (frontale,
triangulaire et avec particule immobile) et il est prouvé que cela est suffisant pour
correspondre aux équations de Navier-Stockes. Pas de code mais l'existence de calculateurs
dédiés est évoquée (RAP-1 ?)
|
| [20] |
Gary Doolen (éditeur) "Lattice gas methods for partial differential equations",
Santa Fe Institute, Studies in the sciences of complexity, Addison-Wesley 1990,
ISBN 0-201-15679-2 ou 0-201-13232-X
Probablement l'un des ouvrages les plus intéressants qui existe. Tous les acteurs du domaine
de la première décade sont présents dans cette collection de papiers, traitant de tous les
domaines, pratiques et théoriques. Par exemple on y trouve le modèle FHP4, sur 8 bits, qui
restaure l'invariance galliléenne (en ralentissant le fluide). La variété des points de vue
et des sujets abordés rend sa consultation impérative, mais pourtant il n'y a pas de code.
|
| [21] |
J. A. Somers & P. C. Rem "Obtaining numerical results from the 3D FCHC
lattice gas" dans Lecture Notes in Physics, T. M. M. Verheggen (ed.),
"Numerical methods for the simulation of multi-phase and complex flows" (1990)
Springer-Verlag, ISBN 0-387-55278-2
Les auteurs proposent une amélioration de la technique de J. P. Rivet pour réduire
la taille de la table des collisions du modèle FCHC par une analyse poussée des
1152 isométries des collisions : la table contient seulement 106496 entrées mais
le code Pascal est assez complexe. Performance de 2Mc/s sur un Transputer à 400 noeuds.
|
| [22] |
Jean-Christophe Culioli "Introduction à l'optimisation" (1994) Ed. Marketing/Ellipses,
ISBN 2-7298-9428-4, ref 519.8 CUL
Sous-titre : "Analyse numérique de systèmes complexes". Présente les techniques de Newton-Raphson,
de dichotomie, de programmation linéaire et dynamique.
|
Autres papiers :
| [23] |
Christopher Adler, Bruce M. Boghosian, Eirik G. Flekkoy, Norman Margolus, Daniel H. Rothman :
"Simulating Three-Dimensional Hydrodynamics on a Cellular-Automata Machine"
à paraître dans Journal of Statistical
Physics (1995)
référence preprint : chaos-dyn/9508001 ou comp-gas/9508001
|
| [24] |
Quian et.al. : Lattice BGK Models for Navier-Stokes Equation,
Europhys.Lett., 17 (6), pp. 479-484 (1992)
|
| [25] |
Norman Margolus : "Integer Lattice Gases",
Phys. Rev. E 55 (April, 1997) 4137-4147.
|
| [26] |
Ales Alajbegovic, Chris Teixeira, David Hill, Andrew Anagnost, Sudheer Nayani and Ram Iyer :
"The study of benchmark laminar flows using DIGITAL PHYSICS"
1997 ASME Fluids Engineering Division Summer Meeting, FEDSM'97,
June 22-26, 1997, FEDSM97-3648
|
| [27] |
Jean-Pierre Boon, Uriel Frisch et Dominique d'Humières : "L'hydrodynamiqe modélisée sur réseau"
dans La Recherche n° 253, avril 1993, volume 54, pages 390-399.
|
| [28] |
Dominique d'Humières, Pierre Lallemand : "Numerical simulations of hydrodynamics with Lattice Gas Automata in two dimensions"
dans Complex Systems 1 (1987) 599-632
|
| [29] |
Dominique d'Humières, Pierre Lallemand, Geoffrey Searby : "Numerical experiments on Lattice Gases : mixtures and galilean invariance"
dans Complex Systems 1 (1987) 633-647
|
| [30] |
Norman Margolus (+?) : "An embedded DRAM architecture for large-scale spatial-lattice computations" (1999)
à paraître (?)
|
| [31] |
Kristian Lindgren, Cristopher Moore et Mats G. Nordahl "Predicting Lattice Gases is P-complete"
Santa Fe Institute Working Paper 97-04-034.
|
| [32] |
D. d' Humières and P. Lallemand : "Numerical simulations of hydrodynamics
with lattice gas automata in two dimensions."
dans Complex Systems, 1:599, 1987.
|
| [33] |
"GA-586ATE users manual, 1st edition"
manuel de carte mère pour PC, 1995.
|
| [34] |
Intel : "Pentium II Processor Developper's Manual"
référence 243502-001, octobre 1997
|
| [35] |
Bruce M. Boghosian, Jeffrey Yepez, Francis J. Alexander, Norman H. Margolus : "Integer Lattice Gases"
comp-gas 9602001 (15 fevrier 1996)
mise à jour le 22 novembre 1998
|
| [36] |
"Benchmark for the simulation of the incompressible flow around a cylinder", 1996
http://gaia.iwr.uni-heidelberg.de/~ture/papers.html
ou in Flow Simulation with High-Performance Computers II,
Notes on Numerical Fluid Mechanics, Vol 52, Vieweg 1996
|
| [37] |
J. Hardy, Y. Pomeau & O. de Pazzis : "Time evolution of two-dimensional model system. I. Invariant states and
time correlation functions", 1973
J. Math. Phys. 14, pp. 1746-1759.
|
| [38] |
Fung Funh Lee : "A Scalable Computer Architecture for Lattice Gas Simulations", 1993
Technical Reports : CSL-TR-93-576
décrit "ALGE", un "superordinateur SIMD"
Mémoire de Doctorat de Philosphie, Université de Stanford, départements EE/CS
|
| [39] |
Intel : "Intel Architecture Software Developer’s Manual Volume 2: Instruction Set Reference", 1999
24319102.pdf
|
| [40] |
Kohring, G.A. "Parallelization of short- and long-range cellular automata on scalar, vector, SIMD and MIMD
machines" 1991
Inter. Jour. Modern Phys. 2, 755-772.
|
| [41] |
Brosa, U. and Stauffer, D. "Vectorized multisite
coding for hydrodynamic cellular automata" 1989
Jour. Stat. Phys. 57, 399-403.
|
Liens
Aujourd'hui une grande partie de l'information scientifique circule sur le Web,
pour des raisons de coûts et de facilité d'accès. Une bibliographie est donc incomplète
et il faut mentionner les très nombreuses ressources en ligne que l'on peut trouver
plus ou moins par hasard, et qui ont été accumulées dans les "bookmarks" du navigateur.
Pour des raisons évidentes, les URL collectionnées ici ne sont ni exhaustives ni garanties pour
leur fraîcheur, puisque le travail présenté dans le mémoire a commencé vers 1995, au début de
l'émergence d'Internet comme média pour le grand public. Internet était cependant déjà utilisé
et très utile pour la communauté des chercheurs sur les LGA et on peut remarquer que les sites
comme les pratiques ont peu changé. Les URL ont été vérifiées en mai 2000 et on peut
penser que la plus grande partie sera valable encore pendant plusieurs années.
Programmation PC et architecture :
Usenet :
news:comp.lang.asm.x86 (ou "clax")
C'est là que les "hackeurs", les "demo makers" et autres "code gurus"
apprennent à écrire leurs premières lignes de code en assembleur,
configurer les registres de la carte vidéo, lire et contrôler les périphériques.
C'est ce newsgroup qui a engendré le travail coopératif sur NASM.
Le "rapport signal/bruit" et le niveau peu avancé fait qu'on se tourne
ensuite rapidement vers d'autres ressources plus pointues comme news:comp.arch.
pmode-l@phys.uu.nl :
la "pmode-l", mailing list dédiée à la programmation avancée en mode protégé. On y apprend à passer
en mode protégé "à la main" ou à profiter des trous de sécurité d'un certain système propriétaire grand public.
Plus sérieusement, c'est un point de rencontre de tous les développeurs de kernel.
http://www.cryogen.com/Nasm/
Le site officiel de NASM, l'assembleur fait par et pour les gens qui programment les
x86 en assembleur.
Contributeurs de NASM et autres gurus de la programmation en assembleur (ne sont ici que les meilleurs) :
http://www.geocities.com/SiliconValley/Peaks/8600/device.html,
http://www.erols.com/johnfine/ : John S. Fine" (johnfine@erols.com)
Alex Verstak (averstak@vt.edu)
http://bphantom.hypermart.net/ : "Black Phantom" (vadim@arx.com)
http://www.azillionmonkeys.com/qed/asm.html : Paul Hsieh (qed@pobox.com)
http://www.azillionmonkeys.com/qed/cpujihad.shtml : la jihad des CPU de 7ème génération
http://www.azillionmonkeys.com/qed/optimize.html : discussion sur la supériorité du codage en assembleur
http://www.azillionmonkeys.com/qed/p5opt.html : astuces de codage pour le Pentium par Paul Hsieh
Terje Mathisen (Terje.Mathisen@hda.hydro.com) (voir sur comp.arch)
http://www.x86.org/,
http://www.sandpile.org/ :
ressources indépendantes sur les
architectures x86 (à consulter absolument avant de programmer !)
http://www.ddj.com/ftp/ :
Dr. Dobb's Source Code archive : plein de morceaux croustillants !
http://www.simtel.net/simtel.net/msdos/index-msdos.html et
http://oak.oakland.edu/simtel.net/ :
Simtel.net FTP shareware archive (certains avec source commentés)
http://www.agner.org/assem :
Les précieux conseils d'Agner Fog
http://www.cs.virginia.edu/stream/ :
John McCalpin
(john@mccalpin.com)
développe depuis 1991 le benchmark STREAM, permettant de comparer des architectures
de manière totalement objective : en mesurant la bande passante de la machine,
disponible à partir de sources en C non optimisés. On dispose ainsi non pas de
la puissance de "crête" mais de la puissance "brute" du système, celle qu'un utilisateur
moyen accède dans la pratique.
http://www.senet.com.au/~cpeacock :
page de Craig Peacock sur la programmation des interfaces et périphériques (PDF et HTML pour contrôler
le port parallèle, le clavier, la souris, le port USB, les interruptions...)
http://www.cs.wisc.edu/~glew/ :
Andy Glew (glew@cs.wisc.edu), impliqué dans l'acceptation du MMX par Intel et dans
le coeur du P6, est une des figures de comp.arch. Ses opinions sur la programmation et les architectures
des ordinateurs le placent en opposition de la culture "Patterson & Hennessy".
Oui, il y a quelqu'un de compétent travaillant pour Intel... Si au moins il était écouté !
http://research.microsoft.com/~gbell/Computer_Structures__Readings_and_Examples/contents.html :
Gordon Bell (qui a créé le prix du même nom) a mis en ligne un de ses livres, introuvable
actuellement, qui est une sorte de pierre de Rosette pour la paléoinformatique comparée.
L'histoire des ordinateurs et l'étude de nombreux cas devrait être un module obligatoire dans
une formation d'informaticien !
http://www.cs.cmu.edu/afs/cs/user/ralf/pub/WWW/files.html :
Ralph Brown a créé et entretenu LA référence sur l'architecture logicielle des PC,
en réunissant et en documentant des milliers d'appels systèmes de MSDOS et d'autres
logiciels similaires (Windows, TSR, Virus, utilitaires, DOS-extenders...). Indispensable.
Intel:
http://developer.intel.com/drg/pentiumii/appnotes/index.htm : Notes d'applications pour le PentiumII.
http://developer.intel.com/design/pentiumII/manuals/243502.htm : Manuel du développeur pour le PentiumII
http://developer.intel.com/design/mmx/manuals/ : Manuels pour développer avec les instructions MMX
VESA :
http://www.monstersoft.com/tutorial1/VESA_info.html
http://mirriwinni.cse.rmit.edu.au/~steve/vbe/vbe20.htm :
"VESA BIOS EXTENSION(VBE) Core Functions with DJGPP Code" ou comment accéder aux modes vidéo haute résolution en assembleur...
http://www.gdsoft.com/swag/downloads.html :
"SWAG" pour "SourceWare Archive Group",
plein d'algorithmes et d'utilitaires pour Turbo Pascal/PC. Un des derniers vestiges de la culture "shareware" et "BBS".
Au lieu de réinventer la roue, il suffit de la copier :-)
http://www.phoenix.gb.net/x86/ :
Page de Win32NASM, pour programmer en assembleur sous Windows, mais en mieux !
Automates cellulaires et Gaz sur Réseau :
Usenet :
news:comp.theory.cell-automata
et news:comp.theory.dynamic-sys
http://www.cs.runet.edu/~dana/ca/cellular.html :
Page dédiée aux automates cellulaires et à Cellang
Page de Bruce Boghossian, travaillant pour Thinking Machines Corp
(avant sa fermeture) et responsable de la CA-list
http://physics.bu.edu/~bruceb/
http://physics.bu.edu/~bruceb/MolSim/ :
"Mesoscale Modeling of Amphiphilic Fluid Dynamics" (transition de phase en 3D)
Homepage d'Oleh Baran, travaillant sur les LGA :
http://www.physics.mcgill.ca/WWW/oleh/Welcome.html
pre-print archive :
Avant d'être envoyés à des publications périodiques sur papier,
les chercheurs soumettent leurs papiers à ces sites permettant d'effectuer
des recherches documentaires sur des sujets pointus. Les serveurs
sont souvent chargés car les documents comme les pages sont générés
à la volée à partir d'une base de donnée et transformés en une grande
variété de formats (PS, PDF, DOC etc) avant d'être transférés.
http://www.arc.umn.edu/publications/preprints/,
http://xyz.lanl.gov,
http://xxx.lanl.gov/archive/cond-mat
miroir à Jussieu :
http://xxx.lpthe.jussieu.fr,
http://fr.arXiv.org/,
http://fr.arXiv.org/find/cond-mat/
http://www.ph.ed.ac.uk/~jmb/thesis/tot.html :
thèse de James M. Buick, calculant FHP-3 sur une CM200 à Edinburgh.
http://poseidon.ulb.ac.be/lga.html :
"CNLPCS: Unité Automates de Gaz sur Réseau".
L'Université Libre de Bruxelles a un département actif dans le domaine des gaz sur réseaux,
les systèmes dynamiques, non linéaires et adaptatifs.
Site web de la CAM8 :
http://www-im.lcs.mit.edu/
http://www.im.lcs.mit.edu/broch/ (quelques exemples hauts en couleurs)
http://zanzibar.mit.edu/ (serveur sporadiquement éteint)
dédié aux applications géophysiques des LGA (infiltration dans les roches etc)
http://www.wizard.com/~hwstock/saltfing.htm
Exposé des travaux de Haarlan Stockman. C'est probablement le seul scientifique qui soit aussi impliqué dans
la vitesse de son code, car c'est aussi un codeur système engagé (il a écrit pour la première fois un code
de calcul de l'ensemble de Mandelbrot en virgule fixe pour 386 en 1986, paru au Doctor Dobb's Journal)
http://www.fuji-ric.co.jp/complex/complex/LGA/result/flatplate.html : (en japonais)
"Behind Flat Plate Flow", travaux des laboratoires Fuji au Japon : même les Japonais utilisent les LGA !
http://www.tele.unit.no/akustikk/person/kristiansen/sudosparrow.html
"The Sudo/Sparrow lattice gas model" : application des LGA à l'acoustique.
http://www.obs-nice.fr/cassini/HTML_FR/rivet.html
"NON-LINEAR DYNAMICS AND TURBULENCE APPLIED TO FLUIDS IN ASTRO- AND GEO-PHYSICS"
L'observatoire de Nice a été parmi les premiers laboratoires, avec l'Ecole de Physique-Chimie
de Paris, à travailler sur les modèles "FHP" et "FCHC" vers 1980. Ils ont activement participé
à l'élaboration et à la validation de la théorie FHP (voir thèse 1982 à Jussieu).
http://www.tu-bs.de/institute/WiR/weimar/ZAscript/ :
"Simulation with Cellular Automata" par
Jörg Weimar, une étude générale des possibilités et des recherches sur les automates cellulaires.
http://www.exa.com :
Spinoff du MIT, exploite une version contestée de Lattice Bolzman en 3D
pour des applications industrielles. En pratique les résultats sont à la hauteurs des milliers d'heures-CPU
qui sont souvent nécessaires à une simulation à grand nombre de Reynolds...
http://amber.aae.uiuc.edu/~m-selig/ads/coord_database.html
"UIUC Airfoil Coordinates Database" : base de donnée de profils vectoriels d'ailes d'avions. J'y ai contribué
avec un repackaging des données avec visualisation sous X et MSDOS.
Divers :


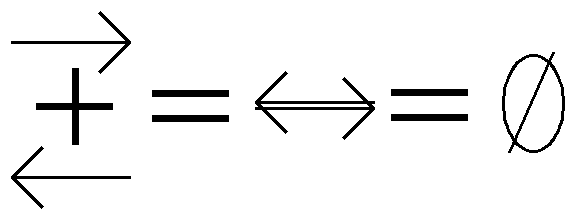
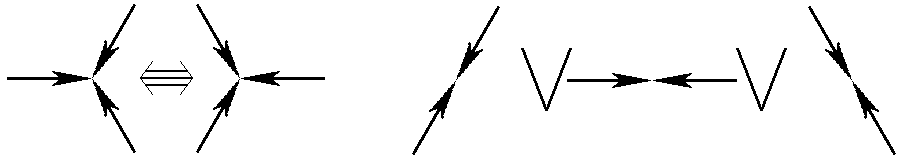
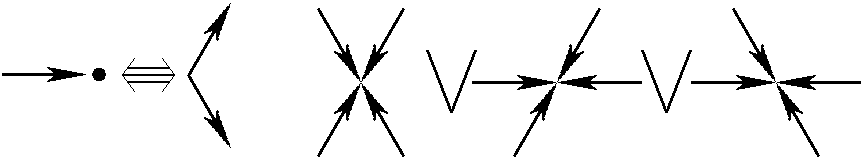
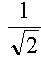
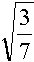
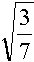
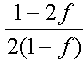
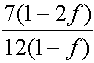
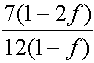
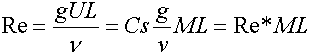

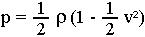

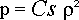
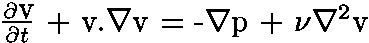
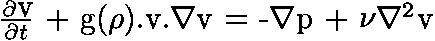


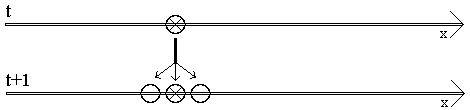
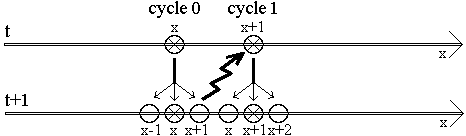






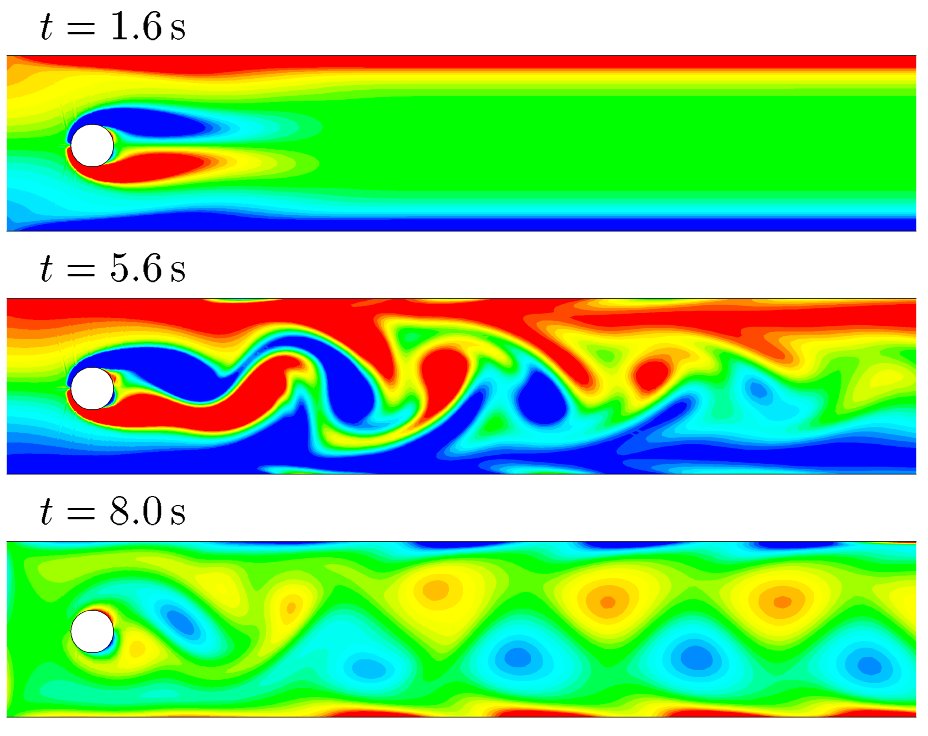
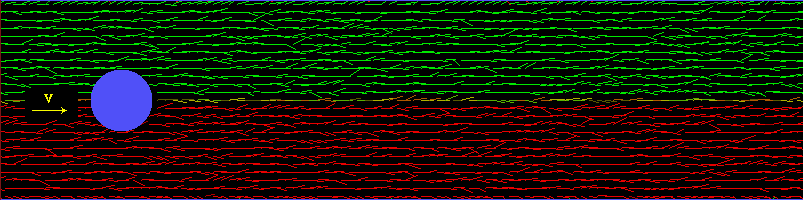

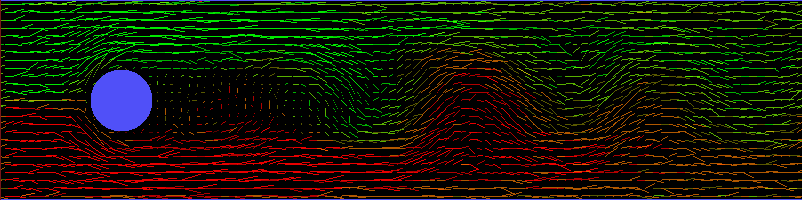
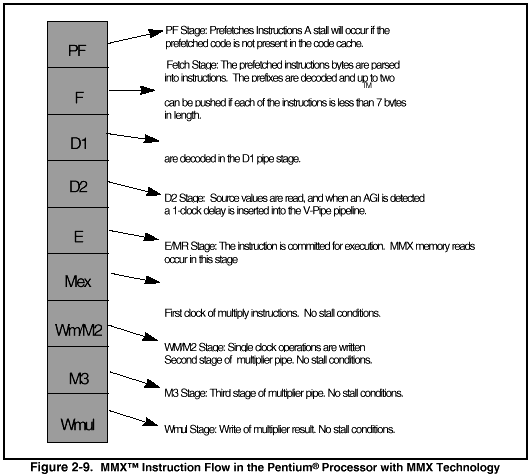
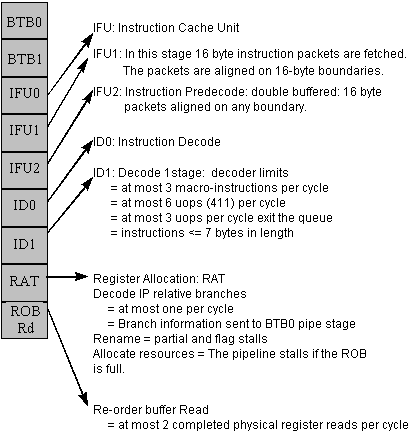
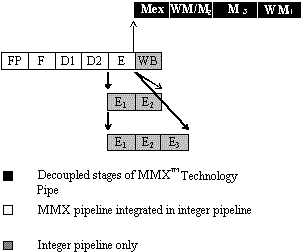
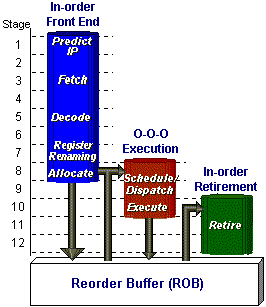










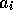 ,
un ensemble de 7 valeurs booléennes représentant l'absence ou la présence d'une particule pour chaque lien
,
un ensemble de 7 valeurs booléennes représentant l'absence ou la présence d'une particule pour chaque lien
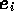 .
.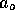 correspond à la particule immobile,
correspond à la particule immobile,
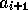 (modulo 6) correspond au lien
(modulo 6) correspond au lien 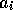 après rotation de 60°.
après rotation de 60°.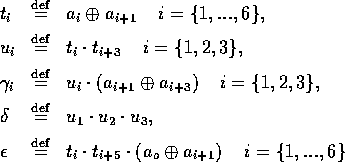
 , a + b,
, a + b, 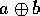 et
et 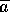 correspondent respectivement aux opérateurs booléens et, ou, ou exclusif et négation.
correspondent respectivement aux opérateurs booléens et, ou, ou exclusif et négation.
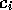 , l'ensemble des variables booléennes représentant les états de sortie, est donné par
, l'ensemble des variables booléennes représentant les états de sortie, est donné par