Voici la version HTML de l'article que j'ai soumis à la rédaction de Pascalissime en septembre 1995. Le source publié avait été légèrement "remanié" par le rédacteur en chef dans le programme principal pour une sombre raison de facilité d'utilisation...
Néanmoins, l'article est paru en février 1996 et occupe 27 pages papier. Aujourd'hui, le but de cette version HTML est seulement d'exposer les principes du modèle et de son implémentation "triviale". J'ai déjà fait plusieurs versions plus évoluées, toutes sous MS-DOS, le texte a donc été juste remis en page.
Depuis la mise en ligne de cet article en janvier 1998,
j'ai pu prendre contact avec François Le Runigo et Umberto d'Ortona (sur la thèse
duquel j'ai fait une erreur de directeur). Et à part les modifications faites
dans le mémoire, rien n'a changé, même pas la table des collisions qui était mauvaise.
Résumé: Cet article présente le modèle et la programmation d'un Gaz sur Réseau permettant de simuler facilement un fluide sur tout ordinateur avec un mode graphique en 256 couleurs.
Mots clés: Gaz sur Réseau, voisinage, plan temporaire, dissymétrie.
Techniques Pascal:
Matériel utilisé: PC 286 VGA & TP6
Champ d'application: Simulation de phénomènes physiques sur petits ordinateurs.
1) Introduction:
Cet article présente un modèle issu de recherches en Mécanique des Fluides (faux : mécanique statistique), permettant de simuler un fluide en effectuant des consultations d'une table, ce qui met la simulation des fluides à la portée des ordinateurs peu puissants.
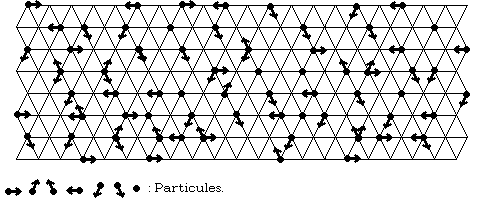
Appelés en anglais Lattice Gas Automata, les Gaz sur Réseau sont des programmes représentant les fluides de manière plus "naturelle" pour les ordinateurs, car toutes les grandeurs sont unitaires. Les particules binaires se déplacent sur un réseau hexagonal, à la manière de boules de billard.
Les programmes de cet article manipulent
facilement dix mille particules avec un vieux PC, alors que les
programmes classiques demandent énormément de
puissance en "virgule flottante".
2) le modèle F.H.P. 3
F,H,P: Messieurs Frisch, Hasslacher et Yves Pomeau ont mis au point et validé cette technique depuis plus de dix ans, mais elle n'est pour l'instant utilisée concrètement nulle part.
Voici le principe de base de cette soufflerie:
on considère le fluide comme constitué de particules
pouvant se déplacer de manière synchrone sur un réseau
hexagonal, à raison d'une seule particule par lien:

Les particules et le réseau sont homogènes: la longeur des liens, la vitesse et la masse des particule sont toutes identiques et unitaires. La quantité de mouvement est rigoureusement conservée, c'est pourquoi la température n'entre pas en jeu.
Les particules se déplacent sur les liens du réseau entre les instants t et t+1. Elles arrivent toutes en t+1 à un noeud, qui concentre six liens. A cet endroit peut se produire une collision si plusieurs particules y arrivent en même temps. Une "table des collisions" détermine leur direction après le choc, pour toutes les possibilités. Les particules sont ensuite envoyées sur les liens correspondants, où elles voyageront entre t+1 et t+2. Le cycle peut donc se résumer en deux phases principales: déplacement et collision.
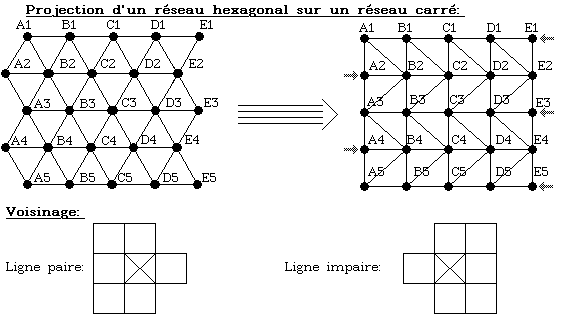
Le réseau des programmes est un tableau
d'octets, où chaque octet représente un noeud.
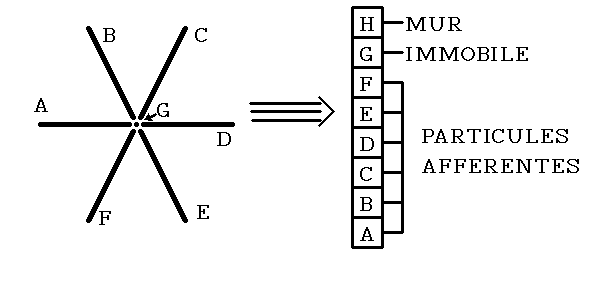
Chaque bit de ce noeud permet de coder une particule ou une fonction
particulière: les six premiers bits (#0 à #5)
représentent les particules reçues par le noeud en t,
le bit #6 représente une particule immobile, et le
bit #7 indique que toutes les particules reçues doivent repartir dans le sens
inverse, pour simuler une collision avec une paroi rugueuse.
Les points importants du programmes sont:
Les conditions initiales sont la place et la direction des particules avant le "calcul", ainsi que la mise en place de parois ou d'obstacles. On initialise aussi la table des collisions, qui a autant d'entrées que de combinaisons possibles à chaque noeud: 256. Toutes ces cases peuvent être remplies par programme, écrites en tant que constante ou chargées à partir d'un fichier.
Si le réseau se trouve dans la mémoire vidéo, toute modification apparaît immédiatement, et il n'y a pas besoin de procédure d'affichage des résultats. Un réseau temporaire est cependant nécessaire pour éviter qu'une particule allant dans le sens du balayage n'aille plus vite qu'une particule allant dans l'autre sens. En effet, l'état d'un noeud en t peut être pris comme son état en t-1 par le noeud de droite, et la particule allant dans la direction A ira plus vite que celle allant dans la direction D.
Les particules "afférentes" sont situées dans le réseau "source" et le résultat des collisions est écrit dans le plan temporaire. On transfère ensuite le tableau temporaire vers le source pour l'étape suivante, ou ce qui est mieux, on renome les tableaux si on utilise des pointeurs pour les accéder.
La boucle de balayage est répétée tant qu'aucune touche n'est appuyée. Cette boucle est orientée sur les lignes paires ou impaires, pour simuler un réseau hexagonal:
La constitution de la table des collisions est la clé de voûte du programme: sans celle-ci, le "fluide" serait comme inerte. Elle nous permet de contrôler les caractéristiques principales du fluide: par exemple, nous pouvons augmenter la viscosité du fluide en diminuant "l'efficacité" des collisions.
La valeur d'entrée est une combinaison de huit bits, correspondant à la configuration des particules arrivant à un noeud. En sortie, la valeur est aussi une combinaison de bits: si un bit est à 1, une particule doit être envoyée au voisin désigné par le rang du bit.
L'ordre des bits est choisi afin que si le tableau n'était pas consulté, aucune modification dans la direction des particules ne serait effectuée.

Le but du tableau est d'introduire une légère dissymétrie, c'est à dire de faire intéragir les particules lors d'un choc en changeant leurs directions, tout en respectant leur nombre et leur quantité de mouvement (leur impulsion). Cette dissymétrie correspond à la réalité, car les particules de l'air ont très peu de chances de se trouver exactement sur la même trajectoire: elles se heurtent donc mais sont désaxées l'une par l'autre, comme des boules de billard.
Le tableau est d'abord rempli par "p[y]:=y", puis on paufine en appliquant certaines règles particulières résumées ici (on ne représente que les vecteurs mouvements):
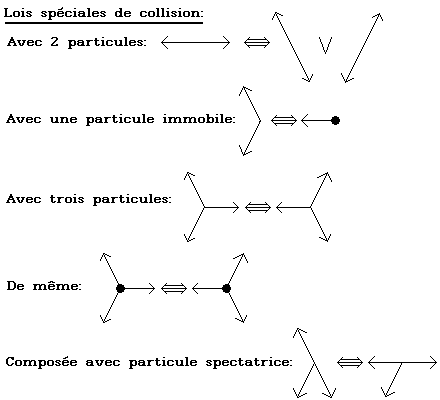
Ces règles respectent une égalité vectorielle plane: nous pouvons aller dans la direction B, puis D, cela revient à aller dans la direction C.
Le modèle FHP "3" est la troisième version du modèle original, qui ne comprenait qu'une seule règle de dissymétrie au départ: celle du choc frontal.
D'autre règles ont été rajoutées pour diminuer la viscosité du fluide, en augmentant les intéractions entre particules. De plus, on a introduit à chaque noeud une particule immobile, qui joue un grand rôle dans l'invariance galiléenne (l'invariance par translation ou rotation dans le repère galiléen).
Les règles de dissymétrie sont appliquées plusieurs fois, si on tient compte des rotations et des homothéties.
Il apparaît cependant que la configuration
du choc frontal entraîne deux possibilités symétriques
et équiprobables: il faut donc deux tables de collision,
comprenant les deux possibilités et que nous
sélectionnons au hasard.
3) L'unité générale:
Cette unité évite d'invoquer
les unités CRT et GRAPH, et gère le mode MCGA
qui est le mode graphique le plus évident dans notre
cas (accès linéaire des pixels en 8 bits).
Il ne sera utilisé à plein rendement que dans
la version en Assembleur de la soufflerie, ce qui permet d'utiliser
n'importe quelle autre librairie graphique à la place de
cette unité dans les deux premiers programmes.
L'initialisation du mode graphique présume
qu'une carte VGA est installée.
La procédure init_palette permet de
visualiser directement la densité de chaque maille de la soufflerie.
"Charge_image" et "Sauve_Image" parlent d'eux-mêmes.
Je me suis servi des procédures du numéro de décembre 1994
pour les dumps en .BMP. J'ai modifié la méthode d'accès
au disque grâce à une boucle "For ... downto" qui traite les
lignes dans l'ordre inverse: on économise ainsi une procédure
de retournement.
"sp" et "gp" sont les primitives graphiques de base:
"sp" est la compression de "Set Point" et remplace
"PutPixel"; de même,
"gp" signifie "Get Point" et retourne le numéro
de la couleur du point désigné.
Aucun test d'intervalle n'est effectué pour ces primitives, car dans les programmes suivants, les coordonnées seront explicitement limitées par les boucles externes.
Des procédures de gestion du clavier sont aussi
redéfinies:
"keypressed" garde la même fonction que dans l'unité CRT,
"stoppe" attend une touche: il est équivalent à
"REPEAT UNTIL KEYPRESSED".
"flush_clv" vide le buffer du clavier: par exemple, il
évite que les touches appuyées avant la fin du programme
n'influent sur l'application qui l'a lancé. De plus, "flush_clv"
est à placer après "stoppe", car celui-ci ne modifie pas le buffer.
Voici l'unité:
(* 001 uGeneral *)
(* Yann GUIDON, 16 juillet 1995 *)
unit uGeneral;
(* manipulation d'images et de fichiers.BMP *)
(* au format 320*200 en 256 couleurs. *)
INTERFACE
const xmax=319;
ymax=199;
var xresolution,yresolution,video_seg:word;
palette:array[0..255,0..2]of byte;
procedure init_mcga;
procedure charge_palette;
procedure init_palette;
procedure charge_image(nom_image:string);
procedure sauve_image(nom_image:string);
procedure sp(x1,y1,coul:word);
function gp(x1,y1:word):byte;
function keypressed:boolean;
procedure stoppe;
procedure flush_clv;
IMPLEMENTATION
(* initialise le mode MCGA *)
procedure init_mcga;
begin
yresolution:=200;
xresolution:=320;
video_seg:=$A000;
(* mode 320*200: *)
asm
mov xresolution,320d
mov ax,13h
int 10h
end
end;
procedure charge_palette;
assembler;
asm
mov si,offset palette
mov cx,768
xor al,al
mov dx,03c8h
out dx,al
inc dx
rep outsb
end;
(* palette pour montrer la densité de chaque maille: *)
procedure init_palette;
var a:byte;
b:word;
begin
(* compte les bits à 1 du numero de la couleur: *)
for b:=0 to 127 do
begin
asm
mov ax,b
mov cx,7d
@label1:
shr al,1
jnc @label2
inc ah
@label2:
loop @label1
mov a,ah
end;
palette[b,0]:=(a*8)+10;
palette[b,1]:=(a*8)+10;
palette[b,2]:=(a*8)+10;
palette[b+128,0]:=40;
palette[b+128,1]:=(a*10)+12;
palette[b+128,2]:=(a*12)+10;
end;
palette[128,0]:=0;
palette[128,1]:=63;
palette[128,2]:=0;
(* couleur de fond: #0=noir *)
palette[0,0]:=0;
palette[0,1]:=0;
palette[0,2]:=0;
charge_palette;
end;
procedure charge_image(nom_image:string);
var fic:file;
i:integer;
j:byte;
begin
assign(fic,nom_image);
reset(fic,1);
seek(fic,1078);
init_palette;
for j:=199 downto 0 do
blockread(fic,mem[video_seg:xresolution*j],xresolution);
close(fic);
end;
procedure sauve_image(nom_image:string);
var fic:file;
i,j:integer;
begin
assign(fic,nom_image);
rewrite(fic,1);
seek(fic,54);
for i:=0 to 255 do
begin
j:=palette[i,2] shl 2;
blockwrite(fic,j,1);
j:=palette[i,1] shl 2;
blockwrite(fic,j,1);
j:=palette[i,0] shl 2;
blockwrite(fic,j,1);
j:=0;
blockwrite(fic,j,1);
end;
for j:=199 downto 0 do
blockwrite(fic,mem[video_seg:xresolution*j],xresolution);
close(fic);
end;
(* Set Point *)
procedure sp(x1,y1,coul:word); assembler;
asm
mov ax,y1
mul xresolution
mov bx,x1
add bx,ax
mov es,video_seg {option 286 et plus!}
mov ax,coul
mov es:[bx],al
end;
(* Get Point *)
function gp(x1,y1:word):byte; assembler;
asm
mov ax,y1
mul xresolution
mov bx,x1
add bx,ax
mov es,video_seg
mov al,es:[bx]
end;
(* Gestion du clavier: *)
(* remplace la fonction standard *)
function keypressed:boolean;
label l;
begin
keypressed:=true;
asm
mov ah,1
int 16h
jnz l
end;
keypressed:=false;
l:
end;
(* attends une touche *)
procedure stoppe;
assembler;
asm
mov ah,1
@suite:
int 16h
jz @suite
end;
(* vide le buffer du clavier: *)
procedure flush_clv;
assembler;
asm
mov ax,40h
mov es,ax
mov al,es:[1Ah]
mov es:[1Ch],al
end;
BEGIN
END.
4) Le programme de base:
Voici un programme d'exemple, où les particules se déplacent dans des tableaux du segment de données. Le résultat est affiché après balayage de ceux-ci.
Les propriétés du fluide sont illustrées par cette expérience: deux mille particules sont placées dans une chambre, qui communique avec une autre par un espace de quelques pixels. Après quelques centaines d'itérations, la densité moyenne des deux chambres est équivalente: le fluide s'est diffusé.
(* 001 GR1.PAS *)
(* Yann GUIDON *)
(* 16 septembre 1995 *)
program gaz_sur_reseau_1;
uses ugeneral;
const max_x=60;
max_y=40;
nb_part=2000;
type chambre=array[0..max_y,0..max_x]of byte;
var t,t2:chambre;
m:byte;
x,y:word;
type collision=array[0..255]of byte;
var p1,p2:collision;
const A=1;
B=2;
C=4;
D=8;
E=16;
F=32;
G=64;
H=128;
procedure init_t2;
var a,b:word;
begin
fillchar(t,sizeof(t),0);
(* parois extérieures *)
for x:=1 to max_x-1 do
begin
t[1,x]:=H;
t[max_y-1,x]:=H;
end;
for y:=1 to max_y-1 do
begin
t[y,1]:=H;
t[y,max_x-1]:=H;
end;
(* paroi de dividion de la chambre en deux *)
for y:=1 to max_y-5 do
t[y,max_x shr 1]:=H;
(* particules dans toutes les directions *)
(* confinées dans une chambre *)
for x:=0 to nb_part do
begin
a:=random(max_y-4)+2;
b:=random(max_x shr 1-4)+2;
t[a,b]:=t[a,b] or (1 shl random(6));
end;
end;
procedure init_p;
begin
(* Constitution pas à pas de la table *)
(* des collision entre particules: *)
(* tous les cas où leur trajectoires *)
(* ne sont pas déviées: *)
for y:=0 to 127 do
p1[y]:=y;
(* collision avec les parois: *)
(* la(les)particules repartent en sens inverse ou sont réfléchies *)
for y:=0 to 7 do
for x:=0 to 7 do
begin
p1[x*8+y+128]:=x+y*8+128;
p1[x*8+y+192]:=x+y*8+192;
end;
(* cas particuliers d'intéractions *)
(* suivant le modèle FHP3: *)
(* 1: collision triangulaire: *)
(* A+C+E<->B+D+F *)
p1[A+C+E]:=B+D+F;
p1[B+D+F]:=A+C+E;
(* 2: collision à 120°: *)
(* une particule sans vitesse intervient *)
p1[A+C]:=B+G;
p1[B+D]:=C+G;
p1[C+E]:=D+G;
p1[D+F]:=E+G;
p1[E+A]:=F+G;
p1[F+B]:=A+G;
p1[A+G]:=B+F;
p1[B+G]:=C+A;
p1[C+G]:=D+B;
p1[D+G]:=E+C;
p1[E+G]:=F+D;
p1[F+G]:=A+E;
(* 3: choc frontal, avec une particule non déviée: *)
p1[A+B+D]:=B+C+F;
p1[A+C+F]:=A+B+E;
p1[B+E+F]:=A+D+F;
p1[A+D+E]:=C+E+F;
p1[C+D+F]:=B+D+E;
p1[B+C+E]:=A+C+D;
(* réciproque: *)
p1[A+C+D]:=B+C+E;
p1[B+C+F]:=A+B+D;
p1[A+B+E]:=A+C+F;
p1[B+D+E]:=C+D+F;
p1[C+E+F]:=A+D+E;
p1[B+E+F]:=A+D+F;
(* maintenant, les tableaux sont traités séparément: *)
p2:=p1;
(* 4: collision frontale: *)
(* cas probabilité #1:*)
(* AD->CF->BE->AD *)
p1[A+D]:=C+F;
p1[F+C]:=B+E;
p1[B+E]:=A+D;
(* cas probabilité #2:*)
(* AD->BE->CF->AD *)
p2[A+D]:=B+E;
p2[B+E]:=C+F;
p2[C+F]:=A+D;
end;
BEGIN
randomize;
init_mcga;
init_palette;
init_t2;
init_p;
(* boucle principale *)
repeat
(* affiche: *)
for y:=1 to max_y-1 do
move(t[y,0],mem[$A000:xresolution*y],max_x);
fillchar(t2,sizeof(t2),0);
for y:=1 to max_y-1 do
begin
if (y and 1)=1 then
begin
for x:=1 to max_x do
begin
(* lignes impaires: *)
m:=t[y,x];
if (m <> 0) then
begin
if (random < 0.5)
then m:=p1[m]
else m:=p2[m];
if (m and H)=H then t2[y,x]:=t2[y,x] or H;
if (m and G)=G then t2[y,x]:=t2[y,x] or G;
if (m and F)=F then t2[y-1,x+1]:=t2[y-1,x+1] or F;
if (m and E)=E then t2[y-1,x]:=t2[y-1,x] or E;
if (m and D)=D then t2[y,x-1]:=t2[y,x-1] or D;
if (m and C)=C then t2[y+1,x]:=t2[y+1,x] or C;
if (m and B)=B then t2[y+1,x+1]:=t2[y+1,x+1] or B;
if (m and A)=A then t2[y,x+1]:=t2[y,x+1] or A;
end;
end;
end
else
begin
for x:=1 to max_x do
begin
(* lignes paires: *)
m:=t[y,x];
if (m<>0) then
begin
if (random < 0.5)
then m:=p1[m]
else m:=p2[m];
if (m and H)=H then t2[y,x]:=t2[y,x] or H;
if (m and G)=G then t2[y,x]:=t2[y,x] or G;
if (m and F)=F then t2[y-1,x]:=t2[y-1,x] or F;
if (m and E)=E then t2[y-1,x-1]:=t2[y-1,x-1] or E;
if (m and D)=D then t2[y,x-1]:=t2[y,x-1] or D;
if (m and C)=C then t2[y+1,x-1]:=t2[y+1,x-1] or C;
if (m and B)=B then t2[y+1,x]:=t2[y+1,x] or B;
if (m and A)=A then t2[y,x+1]:=t2[y,x+1] or A;
end;
end;
end;
end;
t:=t2;
until keypressed;
(* boucle principale *)
flush_clv;
END.
5) Programmation de la soufflerie:
La version "bêta" de notre réseau illustre le principe expliqué en début d'article, mais cette approche naïve se heurte à quelques limitations.
En premier lieu, l'utilisation de trois espaces de mémoire distincts oblige à prendre trop de place pour un seul réseau. Nous pouvons afficher le plan "source" en mémoire vidéo, mais il faudrait se passer d'un plan temporaire trop imposant. Nous utiliserons alors une caractéristique fondamentale du modèle: le traitement est localisé, ce qui veut dire que seule une très petite partie du réseau est considérée à la fois, les particules n'intéragissant qu'avec leurs voisines.
Nous utiliserons deux petits buffers et une variable temporaires, situés dans le segment de données traditionnel, pour conserver les bits D, E et F jusqu'à ce qu'ils ne puissent plus intéragir fâcheusement avec t-1. Les autres bits sont réécris directement, puisqu'ils ne vont pas dans la direction du balayage. Grâce à ces deux structures, qui sont chargées en mémoire cache automatiquement par les processeurs qui en disposent, la taille des données diminue et la vitesse s'accroît.
Les deux buffers gardant les bits E et F s'apparentent en fait à un seul buffer circulaire, mais des complications de gestion ont conduit au modèle présenté ici, qui n'est donc pas la panacée.
La variable temporaire de D conserve deux bits en structure FIFO, qui sont accédés par un décalage à droite. Le traitement local met d'abord (si besoin) le bit #2 à 1, puis le décalage permet de savoir (par le bit #0) si une particule avait été mise en attente avant, pour être déposée plus tard avec les autres qui ne risquaient pas de perturber t-1.
Deuxième remarque: l'invocation de la fonction "Random" prend trop de temps pour ce que nous voulons: brachement ou pas. Nous utiliserons donc une chaîne de bits, initialisés par "Random", que nous balaierons cycliquement par une instruction de rotation. Cette chaîne sera un "word" à cause de mon 286, mais les puristes préfèreront un "longint".
L'instruction de rotation se fera en assembleur, et nous obtiendrons notre bit directement dans le registre d'états: nous pourrons donc effectuer le branchement immédiatement.
La transcription en Assembleur raccourcit le code et accélère encore
l'exécution: c'est important puisque nous manipulons surtout des bits. Mais
la dernière instance dans l'optimisation de ce genre de programme est le
parallélisme: grâce à un processeur 32 bits, nous pourrions traiter les noeuds
par groupes de quatre, et diminuer ainsi le nombre d'accès superflus à la
mémoire.
Notre tunnel de soufflerie peut prendre toute la place de l'écran. Nous y placerons un objet en coupe, qui sera chargé à partir d'une image .BMP. Lorsque vous la créerez, n'oubliez pas que les parois devrons être épaisses et formées avec la couleur #128 (#0 pour le fond bien sûr).
Les particules apparaîtront sur le bord gauche de l'écran. Pour créer cet effet, il suffit de forcer (une fois sur deux grâce à "Rand") le bit 1 de la variable temporaire de D, au début du balayage de chaque ligne.
Dans mes premiers essais de soufflerie, les parois influaient sur les écoulements, car les ondes y étaient réfléchies. Nous considérerons alors que l'écran est "bouclé" sur la hauteur: quand une particule atteint le bord supérieur de l'écran, elle se retrouve en bas. Cela évite qu'elle ne disparaisse par les bords, et fasse chuter la pression.
Voici donc la version Pascal, qui sert de base à la version en assembleur, qui s'exécute beaucoup plus vite:
(* 001 GR2_PAS.PAS *)
(* Yann GUIDON *)
(* 17 septembre 1995 *)
(* version Pascal, à compiler avec l'option 286 *)
Program GR2_PAS;
uses ugeneral;
const
A=1;
B=2;
C=4;
D=8;
E=16;
F=32;
G=64;
H=128;
(* les dissymétrie sont marquées par un 0 devant le nombre: *)
p:array[0..511]of byte=(
(* partie 9->36->18->9 *)
0, 1, 2, 3, 4,066, 6, 7, 8,036,068,038, 12,022, 14, 15,
16,096, 09,037,072,042,013, 23, 24,052,044, 27, 28, 29, 30, 31,
32, 33,065, 35,018,019,011, 39,080,050,021, 43,026, 45, 46, 47,
48, 49,041, 51,025, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63,
64,034, 05, 67,010, 69, 70, 71,020, 73, 74, 75, 76, 77, 78, 79,
040, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95,
017, 97, 98, 99,100,101,102,103,104,105,106,107,108,109,110,111,
112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,
128,136,144,152,160,168,176,184,129,137,145,153,161,169,177,185,
130,138,146,154,162,170,178,186,131,139,147,155,163,171,179,187,
132,140,148,156,164,172,180,188,133,141,149,157,165,173,181,189,
134,142,150,158,166,174,182,190,135,143,151,159,167,175,183,191,
192,200,208,216,224,232,240,248,193,201,209,217,225,233,241,249,
194,202,210,218,226,234,242,250,195,203,211,219,227,235,243,251,
196,204,212,220,228,236,244,252,197,205,213,221,229,237,245,253,
198,206,214,222,230,238,246,254,199,207,215,223,231,239,247,255,
(* rebelotte pour la dissymétrie 9->18->36->9 *)
0, 1, 2, 3, 4,066, 6, 7, 8,018,068,038, 12,022, 14, 15,
16,096,036,037,072,042,013, 23, 24,052,044, 27, 28, 29, 30, 31,
32, 33,065, 35, 09,019,011, 39,080,050,021, 43,026, 45, 46, 47,
48, 49,041, 51,025, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63,
64,034, 05, 67,010, 69, 70, 71,020, 73, 74, 75, 76, 77, 78, 79,
040, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95,
017, 97, 98, 99,100,101,102,103,104,105,106,107,108,109,110,111,
112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,
128,136,144,152,160,168,176,184,129,137,145,153,161,169,177,185,
130,138,146,154,162,170,178,186,131,139,147,155,163,171,179,187,
132,140,148,156,164,172,180,188,133,141,149,157,165,173,181,189,
134,142,150,158,166,174,182,190,135,143,151,159,167,175,183,191,
192,200,208,216,224,232,240,248,193,201,209,217,225,233,241,249,
194,202,210,218,226,234,242,250,195,203,211,219,227,235,243,251,
196,204,212,220,228,236,244,252,197,205,213,221,229,237,245,253,
198,206,214,222,230,238,246,254,199,207,215,223,231,239,247,255);
var
rand,x:word;
retenue_D,y,y2,m:byte;
temp_pair,temp_impair:array[0..xmax+1]of byte;
function rand_bit:boolean; assembler;
asm
xor al,al
rol rand,1
jc @false
inc al
@false:
end;
BEGIN
randomize;
rand:=random(65535);
init_mcga;
charge_image('PROFIL.BMP'); (* votre image de profil *)
fillchar (temp_pair,sizeof(temp_pair),0);
fillchar (temp_impair,sizeof(temp_impair),0);
(* boucle principale *)
repeat
begin
y:=0;
(* lignes impaires: *)
for y2:=1 to (ymax shr 1) do
begin
inc(y);
(* rajoute des particules sur le côté *)
(* en forçant la retenue *)
if rand_bit
then
retenue_D:=2
else
retenue_D:=0;
for x:=1 to xmax-1 do
begin
m:=gp(x,y);
if (m<>0) then
begin
if rand_bit
then m:=p[m]
else m:=p[m+256];
if (m and A)=A then sp(x-1,y,gp(x-1,y)or A);
if (m and B)=B then sp(x-1,y-1,gp(x-1,y-1)or B);
if (m and C)=C then sp(x,y-1,gp(x,y-1)or C);
if (m and D)=D then retenue_D:=retenue_D or 4;
if (m and E)=E then temp_pair[x]:=E;
if (m and F)=F then temp_pair[x-1]:=temp_pair[x-1]or E;
m:=m and (G+H);
end;
retenue_D:=retenue_D shr 1;
if (retenue_D and 1)=1 then m:=m or D;
m:=m or temp_impair[x];
temp_impair[x]:=0;
sp(x,y,m);
end;
(* lignes paires: *)
inc (y);
if rand_bit and rand_bit
then
retenue_D:=2
else
retenue_D:=0;
for x:=1 to xmax-1 do
begin
m:=gp(x,y);
if (m<>0) then
begin
if rand_bit
then m:=p[m]
else m:=p[m+256];
if (m and A)=A then sp(x-1,y,gp(x-1,y)or A);
if (m and B)=B then sp(x,y-1,gp(x,y-1)or B);
if (m and C)=C then sp(x+1,y-1,gp(x+1,y-1)or C);
if (m and D)=D then retenue_D:=retenue_D or 4;
if (m and E)=E then temp_impair[x+1]:=E;
if (m and F)=F then temp_impair[x]:=temp_impair[x]or F;
m:=m and (G+H);
end;
retenue_D:=retenue_D shr 1;
if (retenue_D and 1)=1 then m:=m or D;
m:=m or temp_pair[x];
temp_pair[x]:=0;
sp(x,y,m);
end;
end; (* boucle y *)
(* boucle les particules allant vers le haut, *)
(* les particules allant vers le bas étant bouclées par temp_impair *)
for x:=0 to xmax do
begin
sp(x,xmax-1,gp(x,xmax-1)or gp(x,0));
sp(x,0,0);
end;
end;
until keypressed;
(* boucle principale *)
sauve_image('DUMP.BMP');
flush_clv;
END.
(* 001 GR2_ASM.PAS *)
(* Yann GUIDON *)
(* 18 septembre 1995 *)
(* version assembleur, à compiler aussi avec l'option 286 *)
Program GR2_ASM;
uses ugeneral;
type collision=array[0..511] of byte;
const
A=1;
B=2;
C=4;
D=8;
E=16;
F=32;
G=64;
H=128;
(* les dissymétrie sont marquées par un 0 devant le nombre: *)
p:array[0..511]of byte=(
(* partie 9->36->18->9 *)
0, 1, 2, 3, 4,066, 6, 7, 8,036,068,038, 12,022, 14, 15,
16,096, 09,037,072,042,013, 23, 24,052,044, 27, 28, 29, 30, 31,
32, 33,065, 35,018,019,011, 39,080,050,021, 43,026, 45, 46, 47,
48, 49,041, 51,025, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63,
64,034, 05, 67,010, 69, 70, 71,020, 73, 74, 75, 76, 77, 78, 79,
040, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95,
017, 97, 98, 99,100,101,102,103,104,105,106,107,108,109,110,111,
112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,
128,136,144,152,160,168,176,184,129,137,145,153,161,169,177,185,
130,138,146,154,162,170,178,186,131,139,147,155,163,171,179,187,
132,140,148,156,164,172,180,188,133,141,149,157,165,173,181,189,
134,142,150,158,166,174,182,190,135,143,151,159,167,175,183,191,
192,200,208,216,224,232,240,248,193,201,209,217,225,233,241,249,
194,202,210,218,226,234,242,250,195,203,211,219,227,235,243,251,
196,204,212,220,228,236,244,252,197,205,213,221,229,237,245,253,
198,206,214,222,230,238,246,254,199,207,215,223,231,239,247,255,
(* rebelotte pour la dissymétrie 9->18->36->9 *)
0, 1, 2, 3, 4,066, 6, 7, 8,018,068,038, 12,022, 14, 15,
16,096,036,037,072,042,013, 23, 24,052,044, 27, 28, 29, 30, 31,
32, 33,065, 35, 09,019,011, 39,080,050,021, 43,026, 45, 46, 47,
48, 49,041, 51,025, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63,
64,034, 05, 67,010, 69, 70, 71,020, 73, 74, 75, 76, 77, 78, 79,
040, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95,
017, 97, 98, 99,100,101,102,103,104,105,106,107,108,109,110,111,
112,113,114,115,116,117,118,119,120,121,122,123,124,125,126,127,
128,136,144,152,160,168,176,184,129,137,145,153,161,169,177,185,
130,138,146,154,162,170,178,186,131,139,147,155,163,171,179,187,
132,140,148,156,164,172,180,188,133,141,149,157,165,173,181,189,
134,142,150,158,166,174,182,190,135,143,151,159,167,175,183,191,
192,200,208,216,224,232,240,248,193,201,209,217,225,233,241,249,
194,202,210,218,226,234,242,250,195,203,211,219,227,235,243,251,
196,204,212,220,228,236,244,252,197,205,213,221,229,237,245,253,
198,206,214,222,230,238,246,254,199,207,215,223,231,239,247,255);
var
rand,seg_ligne,x:word;
y:byte;
temp_pair,temp_impair:array[0..xmax+1]of byte;
BEGIN
randomize;
rand:=random(65535);
init_mcga;
charge_image('PROFIL.BMP');
asm
mov ax,seg temp_pair
mov es,ax
xor ax,ax
mov di,offset temp_pair
mov cx,xmax+2
rep stosb
mov di,offset temp_impair
mov cx,xmax+2
rep stosb
(* boucle principale *)
@BOUCLE_EXTERIEURE:
mov seg_ligne,$A000
mov y,99
@BOUCLE_Y:
mov es,seg_ligne
(* PARTIE IMPAIRE: *)
(* force la particule D *)
xor cl,cl
rol rand,1
jnc @pas_retenue1
mov cl,1
@pas_retenue1:
mov bp,1 (* BP est le registre de contrôle de la boucle *)
mov di,xmax+2 (* DI pointe sur le noeud courant *)
mov si,offset temp_impair+1 (* SI pointe sur les bits E et F *)
@BOUCLE_IMPAIRE:
(* Al collectera les bits du noeud courant *)
lodsb
mov byte[si-1],0
(* Ah désignera les bits à envoyer *)
mov ah,byte ptr es:[di]
or ah,ah
jz @vide1
(* consulte le tableau: *)
mov bl,ah
xor bh,bh
rol rand,1
jnc @pas_rol1
inc bh
@pas_rol1:
mov ah,byte[bx+offset p]
(* distribue les bits: *)
shr ah,1
jnc @pas_A1
or byte ptr es:[di-1],A
@pas_A1:
shr ah,1
jnc @pas_B1
or byte ptr es:[di-xmax-1],B
@pas_B1:
shr ah,1
jnc @pas_C1
or byte ptr es:[di-xmax],C
@pas_C1:
shr ah,1
jnc @pas_D1
or cl,2
@pas_D1:
shr ah,1
jnc @pas_E1
or byte ptr ds:[bp+offset temp_pair],E
@pas_E1:
shr ah,1
jnc @pas_F1
or byte ptr ds:[bp+offset temp_pair-1],F
@pas_F1:
shl ah,6
or al,ah
@vide1:
shr cl,1
jnc @pas_retenue_D1
or al,8
@pas_retenue_D1:
stosb
inc bp
cmp bp,xmax
jbe @BOUCLE_IMPAIRE
(* PARTIE PAIRE: *)
xor cl,cl
rol rand,1
jnc @pas_retenue2
mov cl,1
@pas_retenue2:
mov bp,1
add di,2
mov si,offset temp_pair+1
@BOUCLE_PAIRE:
lodsb
mov byte[si-1],0
mov ah,byte ptr es:[di]
or ah,ah
jz @vide2
mov bl,ah
xor bh,bh
rol rand,1
jnc @pas_rol2
inc bh
@pas_rol2:
mov ah,byte[bx+offset p]
(* distribue les bits: *)
shr ah,1
jnc @pas_A2
or byte ptr es:[di-1],A
@pas_A2:
shr ah,1
jnc @pas_B2
or byte ptr es:[di-xmax-2],B
@pas_B2:
shr ah,1
jnc @pas_C2
or byte ptr es:[di-xmax-1],C
@pas_C2:
shr ah,1
jnc @pas_D2
or cl,2
@pas_D2:
shr ah,1
jnc @pas_E2
or byte ptr ds:[bp+offset temp_impair+1],E
@pas_E2:
shr ah,1
jnc @pas_F2
or byte ptr ds:[bp+offset temp_impair],F
@pas_F2:
shl ah,6
or al,ah
@vide2:
shr cl,1
jnc @pas_retenue_D2
or al,8
@pas_retenue_D2:
stosb
inc bp
cmp bp,xmax
jbe @BOUCLE_PAIRE
add seg_ligne,40
dec y
jnz @BOUCLE_Y
(* envoie les particules en bas *)
push ds
(* pointe sur la première ligne *)
mov ax,0A000h
mov ds,ax
xor si,si
(* pointe sur la dernière ligne *)
add ax,3960
mov es,ax
mov dx,160
@BOUCLE_BAS:
lodsw
mov word[si-2],0
or word ptr es:[si],ax
dec dx
jnz @BOUCLE_BAS
pop ds
mov ah,1
int 016h
jz @BOUCLE_EXTERIEURE
end;
(* boucle principale *)
flush_clv;
END.
6) Les défauts et améliorations:
Le modèle programmé ici a un premier gros défaut: le plan temporaire joue le même rôle qu'une variable temporaire dans l'échange de deux valeurs, parce que les deux bits qui définissent chaque direction de lien peuvent être occupés sans que cela ne dérange le programme. L'effet immédiat est que la viscosité est augmentée: deux particules en choc frontal ne sont déviées qu'une fois sur deux, si elles sont distantes d'un nombre pair de liens. La règle d'une seule particule par lien est donc ignorée.
Je n'ai trouvé aucune technique basée sur la programmation qui permette de résoudre ce problème sans introduire d'autre défaut: il faut donc rééxaminer la théorie attentivement.
Ensuite, il est important de bien définir la "vitesse du son": ce n'est surtout pas la vitesse à laquelle se déplacent les particules, c'est la vitesse de propagation d'un onde dans toutes les directions. Elle a été calculée et mesurée à SQRT(3/7*(l/tau)): elle est donc au moins inférieure à la vitesse d'une particule. Dans la soufflerie numérique, il ne suffira pas non plus d'introduire des particule sur le côté, il faudra plutôt considérer la masse de particules déplacées.
Cela nous amène à la représentation des données: grâce à ce programme, nous pouvons voir directement la densité en chaque point, mais il est parfois préférable de visualiser une direction ou une densité moyenne sur une zone. Le modèle FHP permet cette moyenne par sommation des vecteurs mouvements.
La taille des systèmes que l'on peut étudier est très limitée: avec un réseau d'un million de points, on peut ne peut arriver qu'à 300 Reynolds, alors qu'une aile de 747 en développe 50 millions! Néanmoins, avec quelques efforts, il est sûrement possible de simuler une aile de planeur en modèle réduit.
Et puis, ainsi que je l'ai lu dans les thèses, l'utilisation d'une particule immobile permet de restaurer l'invariance galiléenne. Il est demandé que six particules soient en mouvement et que dix-huit soient immobiles. De même, il est recommandé que la densité soit d'un tiers.
Tous ces défauts ont été résolus dans les modèles actuels, où sont utilisées les approximations de Boltzman pour faire les calculs. Ceux-ci sont en virgule flottante, mais la définition est très fine.
Le modèle FHP possède toutefois des atouts décisifs par rapport aux modèles classiques: en plus de son large domaine d'application et sa facilité et sa souplesse de mise en oeuvre, aucune approximation n'est effectuée, comme pour les équations de Navier-Stockes, donc aucune erreur n'est amplifiée et la matière est absolument conservée. De plus, l'introduction d'une dissymétrie rend le modèle indéterministe et le fait mieux correspondre à un fluide visqueux dissipatif: l'évolution est irréversible dans le temps, contrairement à Navier-Stockes. En plus, malgré ce que l'on pourrait croire, la propagation d'une onde sur le réseau hexagonal produit bien des cercles, et non des hexagones.
Pierre Curie a dit: "La dissymétrie des effets se trouve dans les causes." L'approche de ce modèle ne considére plus une masse de fluide comme un volume se pliant aux lois des Mathématiques, mais s'intéresse au comportement local de ses éléments, pour dégager ses spécificités.
7) Où trouver des informations ?
"La Revue du Palais de la Découverte" a présenté le modèle FHP en avril 1987.
Les documents qui m'ont aidé ensuite pour cet article se trouvent
dans les bibliothèques de l'université JUSSIEU (Paris 6-7), surtout en
section "Enseignement Mathématiques et Informatique" (tour 56) qui est en accès
libre. La partie "Recherche" dispose d'après le fichier de la majorité des
titres à ce sujet.
J'ai pu consulter deux thèses de doctorat de Mécanique des Fluides de 1994
(Paris 6), ayant comme maître de thèse le professeur Zaleski:
- Umbert d'Ortona:"Hydrodynamique et Gaz sur réseau",
- Valérie Pot:"Etude microscopie du transport et du changement de phase en
milieu poreux par la méthode des gaz sur réseau".
Ces ouvrages expliquent l'évolution et les applications des Gaz sur Réseau.
Le mensuel "Pour La Science" parle parfois de ce sujet, dans la rubrique "Actualité" lorsqu'un nouveau modèle est mis au point. Des sujets voisins y sont aussi présentés, dans les "Récréations Informatiques".
Existe-t-il un forum sur Internet pour les Gaz sur Réseau ?
8) Conclusion
Le modèle FHP présenté ici permet de simuler un fluide respectant les
équations des gaz parfaits et de Navier-Stockes, sans les utiliser.
De nombreuses améliorations ont validé le modèle, mais aucune application
concrète n'a encore vu le jour.
Les programmes proposés ne prétendent pas être scientifiques, car je n'ai
pas encore réuni toutes les informations nécessaires pour utiliser les gaz sur
réseau dans les règles de l'art.
La facilité d'utilisation de ce modèle le met à la portée des programmeurs ou graphistes qui essaient de fabriquer des images réalistes, mais qui n'ont pas de gros ordinateur. De plus, en modifiant judicieusement la table des collisions, nous pouvons changer les caractéristiques du fluide, et simuler d'autres phénomènes.
J'avais prévu initialement pour cet article de nombreux autres exemples de modèles à "intéractions courtes", qui pourront faire l'objet d'un article ultérieur: "Les Automates Cellulaires".