 Picture 1 |
 Picture 2 |
2007/01 : An interactive JavaScript version is now online at
http://ygdes.com/3r/
This algorithm is also featured in the 4th edition of David Salomon's book
"Data Compression: The Complete Reference", described at
http://www.davidsalomon.name/DC4advertis/DComp4Ad.html
Most compressors require a significant amount of code as well as a minimum amount of input data to become effective (notably PPM, LZ or BWT-based bzip2). The "Recursive Range Reduction" algorithm ("3R" for short) on the other hand operates on small, specific datasets with a decent efficiency and reduced coding effort. This is attractive for embedded systems or when it is not possible to include an external compression library. "3R" was designed to reduce the size of histograms but it also applies, to a certain extent, to similar kinds of data, such as FFT or DCT results.
The 3R algorithm appeared during the design of a lossless signal compression algorithm, as I wanted to store some occurence counts in a more efficient way than a simple array. Using existing algorithms would be useless, as most of them operate on bytes (while histograms can contain very large numbers) and are quite complex for such a simple task.
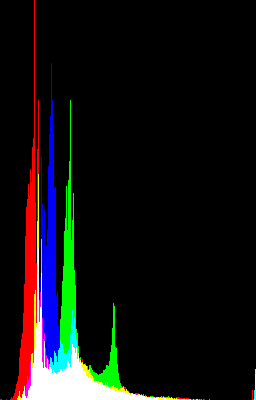
Picture 1 shows the histogram of picture 2 and can be considered as a typical use of the 3R algorithm. Other sources of statistics and physical measures can exhibit similar characteristics.
 Picture 1 |
 Picture 2 |
This kind of information does not correspond to the usual signal types and is not efficiently processed by the classical algorithms that deal with text, cyclic or random signals. There is some kind of correlation that is difficult to model but it is not random. Rice codes seem unefficient when there is a smooth transition between two consecutive data. The size of the generated prefix codes would then not vary much locally, resulting in lost opportunities of dropping bits. Encoding the difference between two data, on the other hand, expands the coded data by one bit in the worst case because it creates negative numbers.
After evaluating many possibilities, the "Recursive Range Reduction" algorithm appeared. It is not a magic wand, but it is based on simple observations and it can be useful where other algorithms fail.
As the name says, it's a recursive algorithm that restricts the range of numbers, or more precisely, the number of bits that represent them. It can operate on any data width, not only bytes. In order to explain how it works, I will first show how to encode a sorted list of numbers with the "range reduction" trick ("RR"), then how to apply this trick to an unsorted list with a recursive approach (hence the third 'R'). Finally, 3R will be adapted to the encoding of a 2-D DCT matrix in JPEG, replacing the Huffman/VLC or arithmetic algorithms.
The heart of this coding algorithm can be best understood by analyzing the properties of a list of positive, sorted, decreasing numbers. If the input data potentially contains negative numbers, then the list shall be preprocessed: either by folding (rotating the sign bit into the LSB of the number) or by adding an offset to all the numbers.
If the list decreases, then the number of significant bits of consecutive values decreases as well. The idea behind RR is well understood: useless MSBs are discarded. However there are still "useful" MSBs because we need some way to know the size of the next number. In particular, the leading bit (which is always set) is not discarded.
In order to know the size of a value, one has to know it but we only know its upper limit, as given by the previous value. Yet this is enough to determine how many bits must be extracted from the compressed bitstream. The number of remaining non-significant MSBs indicates how many bits must be substracted from the current "range counter" before the next value is extracted.
This method can be viewed as using the Rice codes in order to indicate not the size of the number, but the number of bits that are not used by the next number in the list. The curious "delay" effect (the Rice code applies to the next number, not the currently decoded one) introduces some gotchas when analyzing the RR algorithm from the classical point of view of prefix codes. Of course, these "delta" numbers, encoded with other methods, could be moved somewhere else in the stream, but that would make the program more complex for almost no benefit in most situations.
Since the size prefixes are moved before the actual numbers, we must not forget the first one. Usually, the value of the first number of the list is not known so we must start the compressed bitstream with the size (number of bits) of this first number. Usually, it is bound by another known value so we can encode it with a normal binary number in a fixed size field. However, since the length of the first number is known, we can drop its MSB because it is always set.
Figure 1 shows the similarities between RR and the simplest Rice prefix code on an arbitrary list. This illustrates that the continuity of the input list is exploited and leads to a more compact representation.
S={125, 110, 60, 40, 12, 4, 1}
Rice coding:
0000001111101
0000001101110
00000111100
00000101000
0001100
00100
1
____________________
61 bits
|
RR coding:
0111 (size prefix)
111101 (S[0], implicit MSB is dropped)
1101110 (S[1])
0111100 (S[2])
101000 (S[3])
001100 (S[4])
0100 (S[5])
001 (S[6])
_________________________
43 bits
|
If we consider that S is an array of bytes, then S uses 7*8=56 bits. In this arbitrary example, the Rice-encoded output stream requires 61 bits, where the RR-encoded stream uses 43 bits, sparing 23% of the bits. This includes the 4-bit size header, in order to let S[0] span from 0 to 8 bits. The remaining coding space (values from 9 to 15) will be removed later.
Before we start with the "real thing", let's first define some common code in bitstream.c: the bitstream insertion and extraction routines. They are rudimentary but good enough to debug the following compression parts, and show how they work with the help of some printf().
/*
file bitstream.c
(C) 2003 Yann GUIDON <whygee@f-cpu.org>
Common code for the Range Reduction algorithms
version Sat Dec 27 09:21:56 CET 2003
"int"s are assumed 32-bit and the bitstream
has a byte granularity (this should be endian-proof),
so the largest values are 24 bits wide.
*/
#include <stdio.h> /* for printf */
/* some global data */
unsigned int stream_length; /* number of bytes */
unsigned int shift_count; /* number of bits in the reservoir */
unsigned int reservoir; /* bit accumulator */
unsigned char * stream;
/* bit insertion routine */
void put_bits(unsigned int nb_bits,
unsigned int data) {
int i;
if (nb_bits==0) {
printf("[skipping 0]\n");
return;
}
/* print the number in binary format */
i=nb_bits-1;
do {
putchar(((data >> (i--)) & 1) | '0');
} while (i >= 0);
putchar('\n');
/* merge the input data and the reservoir */
reservoir |= (data << shift_count);
shift_count += nb_bits;
/* sends the bit accumulator, byte per byte */
while (shift_count >= 8) {
stream[stream_length++] = reservoir;
reservoir >>= 8;
shift_count -= 8;
}
/* remove some eventual garbage */
reservoir &= (1U << shift_count) - 1;
}
/* bit extraction routine */
unsigned int get_bits(unsigned int nb_bits) {
unsigned int result;
int i;
if (nb_bits==0) {
printf("[skipping 0]\n");
return 0; /* shortcut */
}
while (shift_count < nb_bits) {
reservoir |= stream[stream_length++] << shift_count;
shift_count += 8;
}
result = reservoir & ((1U << nb_bits) - 1);
reservoir >>= nb_bits;
shift_count -= nb_bits;
/* print the number in binary format */
i=nb_bits-1;
do {
putchar(((result >> (i--)) & 1) | '0');
} while (i >= 0);
return result;
}
The demonstration code will focus on 32-bit integers because it is the most widely used data format. However other data lengths can be used just as easily, provided you are careful with your compiler's behaviour. My old gcc 2.95.3 choked on some expressions with 64 bit data, failing to infer the correct width of intermediary results.
The bistream insertion and extraction functions work with bytes and the bit accumulator must be able to contain up to 8 bits between two calls. My "lazy" code accepts integers up to 32-8=24 bits, which is suitable for most algorithms. The size prefix is log2(24) = 5 bit wide.
The encoder and the decoder are far from complex: it boils down to scanning the list, sending the number with the appropriate number of bits, then reducing the range. The main loop exits when the list reaches zero or the end. The decoder can clear the remaining elements in case of early exit.
The first number is a special case: its size must be computed and the implicit MSB must not be sent (any bit that can be reconstructed must be discarded).
The encoder and decoder are provided in rr_simple.c along with a testbench (rr_testbench.c) that generated the figure 2.
/*
file rr_simple.c
(C) 2003 Yann GUIDON <whygee@f-cpu.org>
version Thu Dec 25 05:28:38 CET 2003
Example source code for the simple
Range Reduction encoder/decoder
*/
#include <stdio.h> /* for printf */
#include <string.h> /* for memset */
#include "bitstream.c"
void encode_RR(int nb_elements, unsigned int *list) {
int i = 1;
int range = 0;
unsigned int t, u;
unsigned int mask;
printf("\nEncoding %d elements : size=", nb_elements);
u = t = list[0];
/* count the number of significant bits */
while (u > 0) {
u >>= 1;
range++;
}
/* output the size prefix */
put_bits(5, range);
if (range > 0) {
/* the first number's MSB is
implicit and discarded : */
printf("0: ");
put_bits(range-1, t);
mask = 1 << (range - 1);
while (i < nb_elements) {
printf("%d: ", i);
t = list[i++];
put_bits(range, t);
/* reduce the range */
while ((t & mask) == 0) {
range--;
if (range == 0) {
printf("[the remaining zeroes are skipped]\n");
return;
}
mask >>= 1;
}
}
}
}
void decode_RR(int nb_elements, unsigned int *list) {
int i = 1, range;
unsigned int t;
unsigned int mask;
printf("\nDecoding %d elements : size=", nb_elements);
range = get_bits(5);
if (range > 0) {
/* get the first word and restore the implicit MSB */
printf("\n0: ");
list[0] = get_bits(range-1) | (1 << (range-1));
mask = 1 << (range - 1);
while (i < nb_elements) {
printf("\n%d: ", i);
t = get_bits(range);
list[i++] = t;
/* range reduction */
while ((t & mask) == 0) {
range--;
/* clear the rest, in case it was not initialized */
if (range == 0) {
if (i < nb_elements) {
printf("[clearing the rest of the destination]\n");
memset(&list[i], 0,
(nb_elements - i) * sizeof(*list));
}
return;
}
mask >>= 1;
}
}
}
else {
memset(&list[0], 0, nb_elements * sizeof(*list));
}
}
/*
file rr_testbench.c
(C) 2003 Yann GUIDON <whygee@f-cpu.org>
version Sat Dec 27 07:10:47 CET 2003
Testbench for the Range Reduction encoder/decoder
compile with
gcc -o rr rr_testbench.c
or
gcc -DPHASING -o rr rr_testbench.c
*/
#include <stdio.h> /* for printf */
#ifndef PHASING
#include "rr_simple.c"
#else
#include "rr_phasing-in.c"
#endif
/* these data shall not be larger than 24 bits */
unsigned int S[16]={ 0xFFFFFF, 0xFFFFFF, 0xFFFFFF,
0x30, 0x20, 3, 2, 1, 1, 1, 1, 0, 0, 0, 0, 0};
unsigned int T[16];
unsigned char bitstream[1000];
int main() {
/******** Encoding ********/
/* initialize the output stream */
stream = &bitstream[0];
stream_length = 0;
shift_count = 0;
reservoir = 0;
encode_RR(16, &S[0]);
encode_RR( 5, &S[10]);
encode_RR( 1, &S[8]);
encode_RR(10, &S[0]);
printf("\nResult : %d bits\n\n",
shift_count + (stream_length << 3));
/* flush the reservoir */
if (shift_count > 0)
stream[stream_length++] = reservoir;
/******** Decoding ********/
/* seek to the start */
stream_length = 0;
shift_count = 0;
reservoir = 0;
decode_RR(16, T);
decode_RR( 5, T);
decode_RR( 1, T);
decode_RR(10, T);
return 0;
}
Encoding 16 elements : size=11000 0: 11111111111111111111111 1: 111111111111111111111111 2: 111111111111111111111111 3: 000000000000000000110000 4: 100000 5: 000011 6: 10 7: 01 8: 1 9: 1 10: 1 11: 0 [the remaining zeroes are skipped] Encoding 5 elements : size=00001 0: [skipping 0] 1: 0 [the remaining zeroes are skipped] Encoding 1 elements : size=00001 0: [skipping 0] Encoding 10 elements : size=11000 0: 11111111111111111111111 1: 111111111111111111111111 2: 111111111111111111111111 3: 000000000000000000110000 4: 100000 5: 000011 6: 10 7: 01 8: 1 9: 1 Result : 249 bits Decoding 16 elements : size=11000 0: 11111111111111111111111 1: 111111111111111111111111 2: 111111111111111111111111 3: 000000000000000000110000 4: 100000 5: 000011 6: 10 7: 01 8: 1 9: 1 10: 1 11: 0[clearing the rest of the destination] Decoding 5 elements : size=00001 0: [skipping 0] 1: 0[clearing the rest of the destination] Decoding 1 elements : size=00001 0: [skipping 0] Decoding 10 elements : size=11000 0: 11111111111111111111111 1: 111111111111111111111111 2: 111111111111111111111111 3: 000000000000000000110000 4: 100000 5: 000011 6: 10 7: 01 8: 1 9: 1 |
The similarities between RR and the family of Rice codes let me think that some properties are similar as well. For example, Rice codes' ideal input data obey to a Laplacian distribution. Parallelly, RR obtains the best data size reduction when encoding an exponentially (base 2) decreasing list of numbers.
These two algorithms remain very distinct because of RR's limitation on sorted positive numbers. Random data with Laplacian distribution are also different from an exponentially decreasing list, but if RR can't encode the same data, it could be used to encode its distribution.
There are two cases where RR is under-efficient: when the list decreases very abruptly or very slowly.
It is obvious that when the list drops from one number to another by more than a few bits, these bits will still be present in the second number. This is a kind of "shadow" or "delay" effect that reduces the encoding efficiency. More complex encoding, like Rice-Golomb codes with various values of k can reduce the loss but will add some significant overhead on the other numbers of the list that don't decrease as much.
Slowly decreasing lists are a worse case with less size reduction. In this case, encoding the difference between consecutive numbers is more efficient, especially when the numbers are large.
However, RR still behaves well when dealing with real-world data, even though it won't do wonders. When facing non-ideal data, little space is gained, but no bit is added (except for the size header). The range reduction algorithm is only an encoder and its efficiency depends on the ability of the pre-processing step to match RR's "exponential" needs.
Many existing methods can potentially increase the compression efficiency, depending on the characteristics of the encoded data and the actual compression gains.
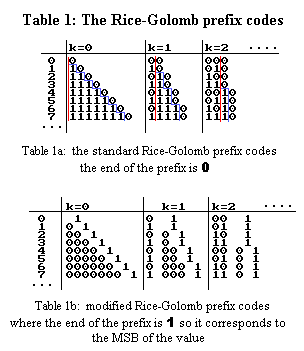
One idea is to use different prefix codes, such as the more general Rice-Golomb family as shown in Table 1. Table 1a shows the classical form but some fields must be inverted (see Table 1b with the bold zeroes) to match the representation of positive integer numbers.
The original RR algorithm uses a special case of the Golomb codes where k=0 (the "Rice" code) but k could have another value to reduce the waste in the very long prefixes, when the list drops drastically. k must be computed in advance and be stored somewhere in a header, adding a computational and size overhead (usually two bits for setting k from 0 to 3). The overhead also depends on the value of k because the prefix size is k bits for each encoded value. The total overhead is then of 2 + (k * nb_elements) and must be justified by a larger compression gain. This happens only when the list drops very drastically or, for the 3R version, when the data is "spiky" such as illustrated by picture 3.
There is some wasted coding space when the input values are just above a power of two. It is possible in average to "win" 0.25 bit per value in a random stream, just because computer's numbers use an integer number of bits to represent values.
The numbers can be combined in order to merge those wasted coding spaces and drop some more bits. Arithmetic codes and range codes can do this, but a much simpler method is almost as efficient and uses only add/subs. These are the "phasing-in codes" that are well covered by Steven Pigeon's page at http://www.iro.umontreal.ca/~pigeon/science/vlc/phasein.html.
This is not the right moment to examine this method, but table 2 and pi_test.c give a good overview. The phasing-in functions have been implemented in phasing-in.c and use bitstream.c to make the code as simple as possible. The modified RR code is provided in rr_phasing-in.c.
| Value | Number of symbols | ||||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 0 | 0 | 0 | 00 | 00 | 00 | 00 | 000 | 000 | 000 |
| 1 | 1 | 10 | 01 | 01 | 01 | 010 | 001 | 001 | 001 |
| 2 | 11 | 10 | 10 | 100 | 011 | 010 | 010 | 010 | |
| 3 | 11 | 110 | 101 | 100 | 011 | 011 | 011 | ||
| 4 | 111 | 110 | 101 | 100 | 100 | 100 | |||
| 5 | 111 | 110 | 101 | 101 | 101 | ||||
| 6 | 111 | 110 | 110 | 1100 | |||||
| 7 | 111 | 1110 | 1101 | ||||||
| 8 | 1111 | 1110 | |||||||
| 9 | 1111 | ||||||||
/*
file pi_test.c
(C) 2003 Yann GUIDON <whygee@f-cpu.org>
version Sat Dec 27 11:33:56 CET 2003
Verifies that phasing-in.c and pi_opt.c
work as expected. More useful than you'd think !
compile with
gcc -o pi_test pi_test.c
or
gcc -DOPT -o pi_test pi_test.c
*/
#ifndef OPT
#include "phasing-in.c"
#else
#include "pi_opt.c"
#endif
unsigned char s[50];
int main() {
unsigned int i, j, range;
stream = &s[0];
/* encode everything */
range=0;
for (i=1; i<; i++) {
printf("\n --- %d --- (range = %d) \n", i, range);
for (j=0; j<i; j++)
pi_put_bits(j, range, i);
if ((1U<<range) <= (i + 1))
range ++;
}
/* check then reinitialise the bitstream */
printf("\nResult : %d bits\n\n", shift_count + (stream_length << 3));
if (shift_count > 0)
stream[stream_length++] = reservoir;
stream_length = 0;
shift_count = 0;
reservoir = 0;
/* check the result */
range=0;
for (i=1; i<=10; i++) {
printf("\n --- %d --- (range = %d) \n", i, range);
for (j=0; j<i; j++)
if (pi_get_bits(range, i) != j) {
printf("\n error !!!\n");
return -1;
}
if ((1U<<range) <= (i + 1))
range ++;
}
return 0;
}
/*
file phasing-in.c
(C) 2003 Yann GUIDON <whygee@f-cpu.org>
version Sat Dec 27 09:21:56 CET 2003
Bitstream insertion/extraction with phasing-in
codes, used by the Range Reduction and 3R algorithms.
Modifications :
- this file replaces bitstream.c
- the "high" parameter is added
- "nb_bits" is replaced by "range",
*/
#include <stdio.h> /* for printf */
#include "bitstream.c"
/* The bit insertion routine */
void pi_put_bits(unsigned int data, /* to be encoded */
unsigned int range, /* number of bits */
unsigned int high) { /* maximal value of data + 1 */
unsigned int t, nb_bits, range2;
unsigned int pi_trig; /* phasing-in variables */
signed int pi_var;
printf("Encoding data=%d with high=%d and range=%d",
data, high, range);
if (range < 1) {
printf(" [range < 1]\n");
return;
}
range2 = range - 1;
/* pi_trig = B = 2^k - b = 2^(k+1) - i */
pi_trig = (1U << range) - high;
pi_var = data - pi_trig; /* i - B */
/* create the phasing-in code: */
if (pi_var < 0) { /* short code */
printf(" [-] ");
nb_bits = range2;
t = data;
}
else { /* long code */
printf(" [+] ");
nb_bits = range;
/* Here, the LSB is put in the MSB (rotated) because otherwise
the decoder would hang when asking for the additional bit !! */
t = ((pi_var >> 1) + pi_trig)
| ((pi_var & 1) << range2);
}
/* this be inlined later */
put_bits(nb_bits, t);
}
/* The bit extraction routine */
unsigned int pi_get_bits(
unsigned int range, /* number of bits */
unsigned int high) { /* maximal value of data + 1 */
unsigned int result;
unsigned int pi_trig; /* phasing-in variables */
signed int pi_var;
printf("Decoding with high=%d and range=%d, ", high, range);
if (range < 1) {
printf("[ range<1 -> result=0 ]\n");
return 0; /* shortcut */
}
result = get_bits(range-1);
/* pi_trig = B = 2^k - b = 2^(k+1) - i */
pi_trig = (1U << range) - high;
pi_var = result - pi_trig; /* i - B */
if (pi_var < 0) { /* short code */
printf(" [-] ");
}
else { /* long code */
printf(" [+] ");
result = (pi_var << 1) + pi_trig + get_bits(1);
}
printf(" result=%u\n", result);
return result;
}
/*
file rr_phasing-in.c
(C) 2003 Yann GUIDON <whygee@f-cpu.org>
version Sat Dec 27 11:47:02 CET 2003
Source code for the Range Reduction
encoder/decoder using phasing-in codes.
*/
#include <stdio.h> /* for printf */
#include <string.h> /* for memset */
#ifndef OPT
#include "phasing-in.c"
#else
#include "pi_opt.c"
#endif
/* The encoding routine : */
void encode_RR(unsigned int nb_elements, unsigned int *list) {
signed int range = 0;
unsigned int i = 1, t, u, mask, high;
printf("\nEncoding %d numbers:\nprefix:\n", nb_elements);
/* create the header */
u = t = list[0];
/* count the number of significant bits */
while (u > 0) {
u >>= 1; /* a binary search */
range++; /* should be faster... */
}
/* output the size prefix with a phasing-in code :
maximal values are 24-bit */
pi_put_bits(range, 5, 25);
if (range > 0) {
/* the first number's MSB is implicit and discarded : */
printf("Initial number (without MSB):\n");
mask = 1U << (range - 1);
pi_put_bits(t & ~mask, range - 1, mask);
/* Start the main loop */
while (i < nb_elements) {
high = t + 1;
t = list[i++]; /* get a new value to encode */
pi_put_bits(t, range, high);
/* reduce the range */
while ((t & mask) == 0) {
range--;
mask >>= 1;
if (mask == 0) {
return;
}
}
}
}
}
/* The decoding routine : */
void decode_RR(unsigned int nb_elements, unsigned int *list) {
unsigned int t, mask, i = 1, range;
printf("\nDecoding %d numbers:\nprefix:\n", nb_elements);
/* get the size prefix */
range = pi_get_bits(5, 25);
if (range > 0) {
mask = 1U << (range -1);
/* get the first word and restore the implicit MSB */
printf("Initial number (without MSB):\n");
t = pi_get_bits(range - 1, mask) | mask;
list[0] = t;
while (i<nb_elements) {
t = pi_get_bits(range, t + 1);
list[i++] = t;
/* range reduction */
while ((t & mask) == 0) {
range--;
mask >>= 1;
if (mask == 0) {
if (i < nb_elements)
/* clear the rest, in case it was not initialized */
memset(&list[i], 0, (nb_elements - i) * sizeof(*list));
return;
}
}
}
}
else {
memset(&list[0], 0, nb_elements * sizeof(*list));
}
}
/*
file pi_opt.c
(C) 2003 Yann GUIDON <whygee@f-cpu.org>
version Sat Dec 27 11:32:09 CET 2003
Bitstream insertion/extraction with phasing-in
codes, used by the Range Reduction and 3R algorithms.
This is a faster, inlined, optimised version.
"range" and "high" are both used to avoid
computing a value that is available somewhere else,
and their coherency is not checked.
*/
#include <stdio.h> /* for printf */
/* some global data */
unsigned int stream_length; /* number of bytes */
unsigned int shift_count; /* number of bits in the reservoir */
unsigned int reservoir; /* bit accumulator */
unsigned char * stream;
/* The bit insertion routine */
void pi_put_bits(unsigned int data, /* to be encoded */
unsigned int range, /* number of bits */
unsigned int high) { /* maximal value of data + 1 */
unsigned int t, nb_bits, range2;
unsigned int pi_trig; /* phasing-in variables */
signed int pi_var, i;
printf("Encoding data=%d with high=%d and range=%d",
data, high, range);
if (range < 1) {
printf(" [range < 1]\n");
return;
}
range2 = range - 1;
/* pi_trig = B = 2^k - b = 2^(k+1) - i */
pi_trig = (1U << range) - high;
pi_var = data - pi_trig; /* i - B */
/* create the phasing-in code: */
if (pi_var < 0) { /* short code */
printf(" [-] ");
nb_bits = range2;
t = data;
}
else { /* long code */
printf(" [+] ");
nb_bits = range;
/* Here, the LSB is put in the MSB (rotated) because otherwise
the decoder would hang when asking for the additional bit !! */
t = ((pi_var >> 1) + pi_trig)
| ((pi_var & 1) << range2);
}
/* print the number in binary format */
i=nb_bits-1;
do {
putchar(((t >> (i--)) & 1) | '0');
} while (i >= 0);
putchar('\n');
/* merge the input data and the reservoir */
reservoir |= (t << shift_count);
shift_count += nb_bits;
/* sends the bit accumulator, byte per byte */
while (shift_count >= 8) {
stream[stream_length++] = reservoir;
reservoir >>= 8;
shift_count -= 8;
}
/* remove some eventual garbage */
reservoir &= (1U << shift_count) - 1;
}
/* The bit extraction routine */
unsigned int pi_get_bits(
unsigned int range, /* number of bits */
unsigned int high) { /* maximal value of data + 1 */
unsigned int result, range2, nb_bits;
unsigned int pi_trig; /* phasing-in variables */
signed int pi_var;
printf("Decoding with high=%d and range=%d, ", high, range);
if (range < 1) {
printf("[ range<1 -> result=0 ]\n");
return 0; /* shortcut */
}
nb_bits = range;
range2 = range - 1;
/* speculatively load "range" bits */
while (shift_count < range) {
reservoir |= stream[stream_length++] << shift_count;
shift_count += 8;
}
result = reservoir & ((1U << range2) - 1);
/* pi_trig = B = 2^k - b = 2^(k+1) - i */
pi_trig = (1U << range) - high;
pi_var = result - pi_trig; /* i - B */
if (pi_var < 0) { /* short code */
printf(" [-] ");
nb_bits = range2;
}
else { /* long code */
printf(" [+] ");
nb_bits = range;
result = (pi_var << 1) + pi_trig +
+ ((reservoir >> range2) & 1);
nb_bits = range;
}
reservoir >>= nb_bits;
shift_count -= nb_bits;
printf(" result=%u\n", result);
return result;
}The PI-codes don't include the upper limit in the coding range. RR's "range" (the last encoded value) must be incremented before the other parameters can be derived. Incrementing by more than one increases the coding space, so we could also encode meta-data such as end-of-stream symbols.
Another issue comes from the order of the bits: table 2 shows the LSB as the trailing bit, but we insert it first. Instead of reversing the order of all the bits (a costly operation), this implementation rotates the word (the LSB/postfix becomes the MSB).
In practice, the phasing-in codes add some complexity and only drop one bit every four elements. The gain is not proportional to the encoded values so the gain appears higher for small elements. Another fraction of bit can be removed by PI-encoding the size header, since the first value doesn't exceed 24 bits. Phasing-in's benefits seem limited but its worst case does not expand, so it works for any dataset. Furthermore, compared to arithmetic codes, it uses "discrete" symbols, so there is no "end of binary stream" to manage.
At first glance, most other methods further increase the coding efforts and add overhead on the encoded bitstream, without ensuring compression benefits. I believe that the RR method is "good" because most methods fail to substancially increase the performance in general cases. Most of RR's characteristics remain to be correctly proved but it seems that "i'm onto something" interesting.
The RR algorithm is limited to sorted data, so one possible approach is to encode and store the permutation of these values. This is not a lightweight process, unless the dataset is very small and the compression gain is very high: table 3 shows the large overhead of this method. Furthermore, the decoding algorithm uses divisions, which is definitely unwanted in high-speed, resource-constrained applications.
(number of elements) |
(number of bits to represent the permutation) |
| 1 | 0 |
| 2 | 1 |
| 3 | 3 |
| 4 | 5 |
| 5 | 7 |
| 6 | 10 |
| 7 | 13 |
| 8 | 16 |
| 9 | 19 |
| 10 | 22 |
| 11 | 26 |
| 12 | 29 |
| 16 | 45 |
| 32 | 118 |
| 64 | 296 |
| 128 | 717 |
| 256 | 1684 |
So here comes the second key "trick": applying a recursive algorithm to create not one sorted list, but a number of smaller sorted lists in a tree. Each node of this tree will split the list, and sum both branches. This way, each sub-list is decreasing: if two numbers a and b are positive, then their sum c is still positive and c > a and b > a.
Now we can "map" our unsorted list to the leaves of a balanced binary tree. The root will contain the sum of all the input numbers. All the paths from the root to any leaf each make a decreasing list which forks at every node, as illustrated in figure 3. Each sublist is encoded with RR but each fork must be processed separately, leading to a recursive algorithm.
A
\
A+B
/ \
B \
A+B+C+D
C /
\ /
C+D
/
D
|
A+B+C+D, A+B, A A+B+C+D, A+B, B A+B+C+D, C+D, C A+B+C+D, C+D, D |
size(A+B+C+D), A+B+C+D, A+B, A, C |
C+D = (A+B+C+D)-(A+B),
==> B = (A+B)-A,
==> D = (C+D)-C
|
Now, the whole tree contains twice the number of elements so one half of them should be discarded. This is possible when knowing both the sum and one of the operands: a simple substraction restores the other operand. When applied recursively, this principle effectively keeps as many output numbers as the input without loss of information.
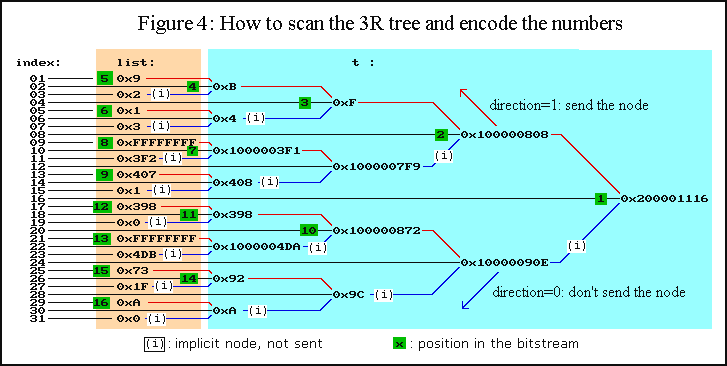
Which branch of the tree must be kept is a question that is best answered by an arbitrary convention. It would "cost" one bit per branch to encode the scanning "direction" and this bit would be wasted if the input data has a uniform probability. This can be optimised in very specific cases only. In the end, figure 4 shows how the tree is built and in what order the data are sent in the bitstream.
The coding and decoding algorithms are not symmetric, unlike the RR algorithm. The decoding side is quite simple: it recursively scans the tree and restores all the nodes' values until it reaches all leaves. This is possible if the encoder has two passes: one that (recursively) computes the nodes' values (leaves to root), then a second pass that re-scans the tree in the decoder's order (root to leaves). For short, the decoder first decodes the root's value from the binary stream, but this sum is known to the encoder only after a first summation pass.
Another difference with RR lies in the allowed input data ranges. The summation of N values eats up log2(N) bits in the root value's size. In the provided code, the 24-bit word size limits the input data to 256 numbers with 16 bits each or sixteen 20-bit numbers for example. Other simplifications limit the number of input elements to a power of two and no range checking is performed.
The recursive functions use an interleaved address space: odd indices point to the leaves (the input data) while even indices point to temporary nodes. The intermediate sums use a space which is dynamically allocated through malloc() but fixed-size versions can use a static array on the stack.
Additionally, the recursive sub-functions use a "direction" parameter so they emulate a pair of coroutines. Whether to use real coroutines or not was dictated by my compiler which corrupted the stack... Special-purpose codes can use a non-recursive algorithm however.
The listing 3r_simple.c implements the general encoder and decoder. A basic testbench is provided by 3r_testbench.c. Many obvious methods exist to adapt and optimise them, for example: clearing the destination before decoding, in order to not process empty data. Phasing-in codes and other tricks are implemented in 3r_phasing-in.c.
/*
3r_simple.c
(C) 2003 Yann GUIDON <whygee@f-cpu.org>
Recursive Range Reduction example source code
created Sun Aug 24 22:16:02 CEST 2003 by whygee@f-cpu.org
version Sat Oct 25 03:32:59 CEST 2003 : cleanup for DDJ
version Wed Dec 31 06:24:57 CET 2003
*/
#include <stdio.h> /* for printf */
#include <stdlib.h> /* for malloc */
#include <string.h> /* for memset */
#include "bitstream.c" /* put_bits & get_bits */
void encode_3R(int nb_elements, unsigned long *list) {
int range = 0;
unsigned long int *t, u, v;
/* recursive summing sub-function */
unsigned long int recursive_sum(int index, int size) {
unsigned long int w, x;
int diff = size >> 2;
if (index & 1)
return list[index >> 1]; /* a leaf was reached */
else {
/* further explore the tree */
w=recursive_sum(index + diff, size >> 1);
x=recursive_sum(index - diff, size >> 1);
w+=x;
t[index >> 1] = w;
return w;
}
}
/* recursive subfunction for the second pass */
void send_stream(int index, int size, int range,
int direction) {
unsigned long int w, mask;
int diff = size >> 2;
if (index & 1) {
/* odd index: we reached a leaf */
if (direction == 1) {
w = list[index >> 1];
put_bits(range, w);
}
}
else {
w = t[index >> 1];
if (direction == 1)
put_bits(range, w);
/* range reduction : */
mask = 1 << (range - 1);
while ((w & mask) == 0) {
range--;
if (range == 0) {
printf("[the remaining zeroes are skipped]\n");
return;
}
mask >>= 1;
}
send_stream(index - diff, size >> 1, range, 1);
send_stream(index + diff, size >> 1, range, 0);
}
}
/**** the function's body : ****/
if ((nb_elements - 1) & nb_elements) {
printf("Error : %d is not a power of 2\n", nb_elements);
exit(-1);
}
t = malloc(nb_elements * sizeof(*t));
if (t == NULL) {
perror("malloc");
exit(-1);
}
/* build the sum tree */
recursive_sum(nb_elements, nb_elements << 1);
/* size of the first number */
u = v = t[nb_elements >> 1]; /* middle of t */
while (u > 0) {
u >>= 1;
range++;
}
/* 5 bits can encode a number from 0 to 24 */
put_bits(5, range);
if (range > 0) {
/* encode the first word without the implicit MSB */
put_bits(range-1, v);
/* explore the tree again */
send_stream( nb_elements >> 1, nb_elements, range, 1);
send_stream((3 * nb_elements) >> 1, nb_elements, range, 0);
}
free(t);
}
void decode_3R(int nb_elements, unsigned long int *list) {
int range;
unsigned long int u;
/* recursive decoding subfunction */
unsigned long int branch(int index, int size,
int direction, int range, unsigned long int difference){
unsigned long int w, t, mask;
int diff = size >> 2;
if (direction == 1)
w = get_bits(range), putchar('\n');
else
w = difference;
if (index & 1) {
/* reaching a leaf of the tree */
printf(" [%2d] = %04lX\n", index >> 1, w);
list[index >> 1] = w;
}
else {
/* range reduction */
mask = 1 << (range - 1);
while (((w & mask) == 0) && (range > 0)) {
range--;
mask >>= 1;
}
t = branch(index - diff, size >> 1, 1, range, 0);
branch(index + diff, size >> 1, 0, range, w - t);
}
return w;
}
/**** the function's body ****/
range = get_bits(5);
putchar('\n');
if (range>0) {
/* restore the MSB of the root's value */
u = get_bits(range - 1);
u |= 1U << (range - 1);
printf("\nrange = %d\n", range);
u -= branch( nb_elements >> 1, nb_elements, 1, range, 0);
branch((3*nb_elements) >> 1, nb_elements, 0, range, u);
}
}
/*
file 3r_testbench.c
(C) 2003 Yann GUIDON <whygee@f-cpu.org>
Recursive Range Reduction,
testbench source code
version Wed Dec 31 02:26:20 CET 2003
compile with:
gcc 3r_testbench.c -o 3r
or
gcc -DPHASING 3r_testbench.c -o 3r
*/
#include <stdio.h> /* for printf */
#include <stdlib.h> /* for malloc */
#include <string.h> /* for memset */
#ifdef PHASING
#include "3r_phasing-in.c"
#else
#include "3r_simple.c"
#endif
/********* Some tests *********/
/* cyclic data */
unsigned long int S[31]={
9, 2, 1, 3, 0xFFFF, 1010, 1031, 1,
920, 0, 0xFFFF, 1243, 115, 31, 10, 0,
9, 2, 1, 3, 0xFFFF, 1010, 1031, 1,
920, 0, 0xFFFF, 1243, 115, 31, 10};
/* what does happen when
only one bit is encoded ? */
unsigned long int T[31]={
0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 1,
0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0};
/* watching the logarithmic
overhead in worst case situation: */
unsigned long int U[16]={
0xBEE0, 0xBEE1, 0xBEE2, 0xBEE3,
0xBEE4, 0xBEE5, 0xBEE6, 0xBEE7,
0xBEE8, 0xBEE9, 0xBEEA, 0xBEEB,
0xBEEC, 0xBEED, 0xBEEE, 0xBEEF};
/* "spiky" input data: */
unsigned long int V[16]={
0, 0xFFFF, 0, 0xFFFF,
0, 0xFFFF, 0, 0xFFFF,
0, 0xFFFF, 0, 0xFFFF,
0, 0xFFFF, 0, 0xFFFF};
/* where the decoded output goes: */
unsigned long int W[32];
unsigned char bitstream[5000];
void test_cpr(unsigned long int *P, int cpt) {
int i, init_size;
init_size = shift_count + (stream_length<<3);
printf("\nInitial data:\n");
for (i=0; i<cpt; i++)
printf("%lX ",P[i]);
printf("\n\nEncoding:\n");
encode_3R(cpt, P);
printf("\n ====> result = %d bits\n\n",
shift_count + (stream_length<<3) - init_size);
}
void test_dcpr(unsigned long int *P, int cpt) {
int i;
printf("\n\nDecoding:\n");
decode_3R(cpt, W);
printf("\nDecoded data:\n");
for (i=0; i<cpt; i++)
printf("%lX ",W[i]);
if (memcmp(W,P,i*sizeof(*P))!=0){
printf("\nError !\n");
exit(1);
}
printf("\n\n ---------------------\n\n");
}
int main(void) {
int i;
/* initialises the binary stream : */
stream = &bitstream[0];
stream_length = 0;
shift_count = 0;
reservoir = 0;
test_cpr(S, 16);
test_cpr(T, 16);
test_cpr(U, 16);
test_cpr(U, 32);
test_cpr(V, 16);
/* look for the effects of rotation */
for (i=0; i< 16; i++)
test_cpr(&S[i], 16);
for (i=0; i< 16; i++)
test_cpr(&T[i], 16);
printf("\n\nTotal result : %d bits\n\n",
shift_count + (stream_length<<3));
/* flush the reservoir */
if (shift_count > 0)
stream[stream_length++] = reservoir;
/* clear the bitstream variables */
stream_length = 0;
shift_count = 0;
reservoir = 0;
test_dcpr(S, 16);
test_dcpr(T, 16);
test_dcpr(U, 16);
test_dcpr(U, 32);
test_dcpr(V, 16);
for (i=0; i< 16; i++)
test_dcpr(&S[i], 16);
for (i=0; i< 16; i++)
test_dcpr(&T[i], 16);
return 0;
}
/*
3r_phasing-in.c
(C) 2003 Yann GUIDON <whygee@f-cpu.org>
Recursive Range Reduction
example source code with phasing-in codes
created Sun Aug 24 22:16:02 CEST 2003 by whygee@f-cpu.org
version Sat Oct 25 03:32:59 CEST 2003 : cleanup for DDJ
version Wed Dec 31 06:52:00 CET 2003 : implemented PI-codes
*/
#include <stdio.h> /* for printf */
#include <stdlib.h> /* for malloc */
#include <string.h> /* for memset */
#ifndef OPT
#include "phasing-in.c"
#else
#include "pi_opt.c"
#endif
void encode_3R(int nb_elements, unsigned long *list) {
int range = 0;
unsigned long int *t, u, v, mask;
/* recursive summing sub-function */
unsigned long int recursive_sum(int index, int size) {
unsigned long int w, x;
int diff = size >> 2;
if (index & 1)
return list[index >> 1]; /* a leaf was reached */
else {
/* further explore the tree */
w = recursive_sum(index + diff, size >> 1);
x = recursive_sum(index - diff, size >> 1);
w += x;
t[index >> 1] = w;
return w;
}
}
/* recursive subfunction for the second pass */
void send_stream(int index, int size, int range,
int direction, unsigned long int last_value) {
unsigned long int w, mask;
int diff = size >> 2;
if (index & 1) {
/* odd index: we reached a leaf */
if (direction == 1) {
w = list[index >> 1];
pi_put_bits(w, range, last_value);
}
}
else {
w = t[index >> 1];
if (direction == 1)
pi_put_bits(w, range, last_value);
/* range reduction : */
mask = 1 << (range - 1);
while ((w & mask) == 0) {
range--;
if (range == 0) {
printf("[the remaining zeroes are skipped]\n");
return;
}
mask >>= 1;
}
send_stream(index - diff, size >> 1, range, 1, w + 1);
send_stream(index + diff, size >> 1, range, 0, w + 1);
}
}
/**** the function's body : ****/
if ((nb_elements - 1) & nb_elements) {
printf("Error : %d is not a power of 2\n", nb_elements);
exit(-1);
}
t = malloc(nb_elements * sizeof(*t));
if (t == NULL) {
perror("malloc");
exit(-1);
}
/* build the sum tree */
recursive_sum(nb_elements, nb_elements << 1);
/* size of the first number */
u = v = t[nb_elements >> 1]; /* middle of t */
while (u > 0) {
u >>= 1;
range++;
}
/* 5 bits can encode a number from 0 to 24 */
pi_put_bits(range, 5, 25);
if (range > 0) {
/* encode the first word without the implicit MSB */
mask = 1U << (range - 1);
pi_put_bits(v & ~mask, range - 1, mask);
/* explore the tree again */
send_stream( nb_elements >> 1, nb_elements, range, 1, v + 1);
send_stream((3 * nb_elements) >> 1, nb_elements, range, 0, v + 1);
}
free(t);
}
void decode_3R(int nb_elements, unsigned long int *list) {
int range;
unsigned long int u, mask;
/* recursive decoding subfunction */
unsigned long int branch(int index, int size,
int direction, int range, unsigned long int difference){
unsigned long int w, t, mask;
int diff = size >> 2;
if (direction == 1)
w = pi_get_bits(range, difference);
else
w = difference;
if (index & 1) {
/* reaching a leaf of the tree */
printf(" [%2d] = %04lX\n", index >> 1, w);
list[index >> 1] = w;
}
else {
/* range reduction */
mask = 1U << (range - 1);
while (((w & mask) == 0) && (range > 0)) {
range--;
mask >>= 1;
}
t = branch(index - diff, size >> 1, 1, range, w + 1);
branch(index + diff, size >> 1, 0, range, w - t);
}
return w;
}
/**** the function's body ****/
range = pi_get_bits(5, 25);
printf("\nrange = %d\n", range);
if (range>0) {
printf("Initial number (without MSB): ");
/* restore the MSB of the root's value */
mask = 1U << (range -1);
/* get the first word and restore the implicit MSB */
u = pi_get_bits(range - 1, mask) | mask;
printf("root = %lX\n", u);
u -= branch( nb_elements >> 1, nb_elements, 1, range, u + 1);
branch((3*nb_elements) >> 1, nb_elements, 0, range, u);
}
}
The 3R algorithm works best when high values are grouped (next to each other). It is also good at discarding consecutive zeroes, almost independently of their location, as shown in figure 5. Here, log2(N) bits are needed (without counting the size header) to locate a single bit out of N elements: that's the theoretic optimum. This case can be generalised to better define and model 3R's properties (any volunteer ?).
Initial data:
0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0
Encoding:
00001
[skipping 0]
0
[the remaining zeroes are skipped]
1
1
0
[the remaining zeroes are skipped]
[the remaining zeroes are skipped]
Result: 9 bits
(including the header's fixed overhead)
Decoding:
00001
[skipping 0]
0
[skipping 0]
[skipping 0]
[skipping 0]
[ 0] = 0000
[ 1] = 0000
[skipping 0]
[ 2] = 0000
[ 3] = 0000
[skipping 0]
[skipping 0]
[ 4] = 0000
[ 5] = 0000
[skipping 0]
[ 6] = 0000
[ 7] = 0000
1
1
0
[ 8] = 0000
[ 9] = 0001
[skipping 0]
[10] = 0000
[11] = 0000
[skipping 0]
[skipping 0]
[12] = 0000
[13] = 0000
[skipping 0]
[14] = 0000
[15] = 0000
Decoded data:
0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0
|
The sums add some overhead which is illustrated, for example, when encoding N values of M bits each. The output bitstream will contain the root with M + log2(N) bits. When averaged over all the stream, the overhead costs N-1 bits, or almost one bit per input value, whatever M. This worst case is more efficient than storing a permutation number or than using Rice codes, and close to Huffman's behaviour. Let's not forget however that most other methods discard the first MSB, which 3R keeps to detect a range reduction.
Another annoying situation occurs when encoding data such as shown in picture 3. This is the histogram of picture 4, which is obtained by contrast correction of picture 2 (histogram flattening). These "spiky" data break the bin-to-bin continuity and are harder to compress, so we must use the more general Rice-Golomb codes. The summation pass is the best place to evaluate which value of k gives the shortest bitstream. A BWT pass could also be applied before 3R !
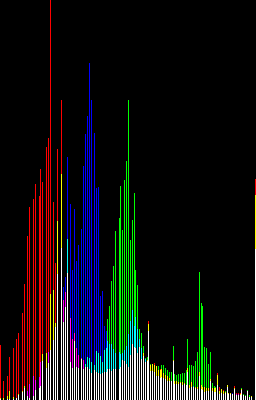 Picture 3 |
 Picture 4 |
3R was initially intended to reduce the size of histograms and can replace the Huffman tree encoding algorithms. This is interesting in the JPEG algorithm, but then we can completely drop Huffman and VLC (Variable Length Codes).
We can use 3R to directly encode the results of the zig-zag scan in each block because 3R is not bound to a specific word length. The granularity of 64 values is handy and provides good local adaptation. The quantization process greatly helps: most high values are grouped and many contiguous values are zeroed. All the values are easily converted to unsigned format.
The zig-zag step can also be dropped because the recursive algorithm is not limited to linear data streams: the 8x8 matrix can be mapped to a "H tree" as shown in figure 6. Each node still corresponds to an addition and this can be extended to other geometries if needed.
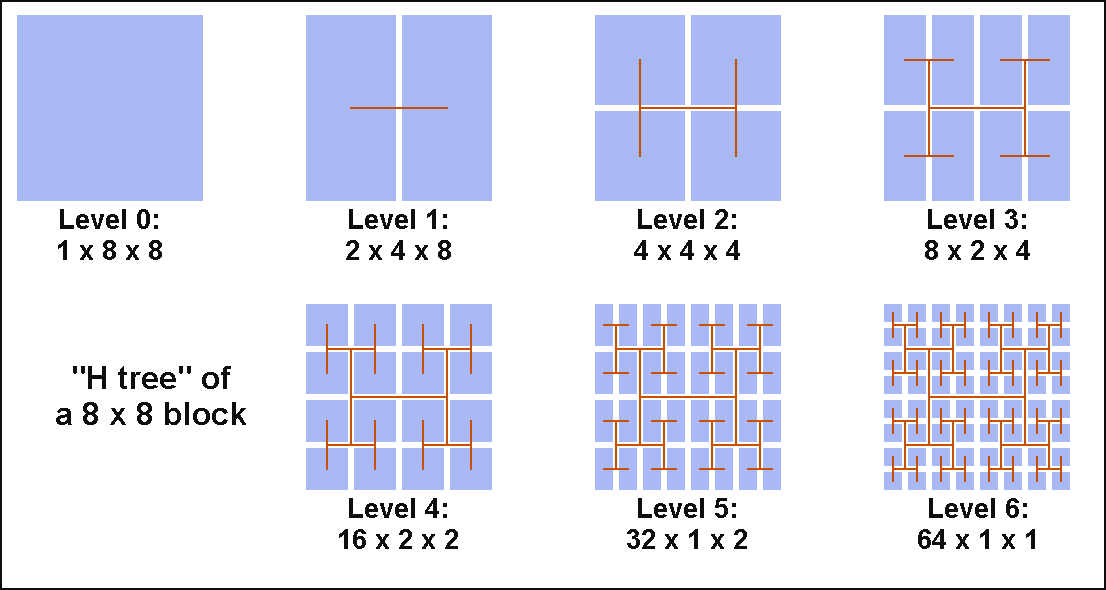
However this is still not optimal because 3R is most efficient when each path from the root to each leaf of the tree corresponds to an exponentially decreasing list. In other words, each branch of a node should statistically have the same weight. This would fit if all the DCT coefficients had the same probability, but the quantization step and the image's properties modifiy this.
So here comes another trick: we can use the Huffman algorithm to build a 2D-tree that best fits the input data's properties. Here the algorithm is extended to the two-dimensional case but it conserves the property that each branch has roughly the same weight. Each path from the root to the leaves has more chances to decrease in log2.
In the case of JPEG and MPEG, the quantization table gives a good static approximation of the relative meaningfulness of each value. Figure 7 shows the conversion of a JPEG luma quantisation matrix into an optimal tree. It is then scanned and sorted so that the output datastream contains potentially lower values, making Golomb codes and Phasing-in codes a bit more efficient.

65536/Q=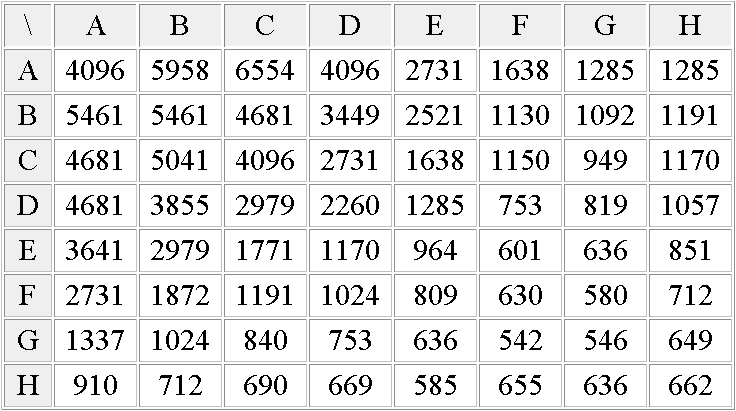
b) Modified, multiplication matrix
(65536 was chosen as an arbitrary scaling constant, it does
not change the resulting tree's topology)
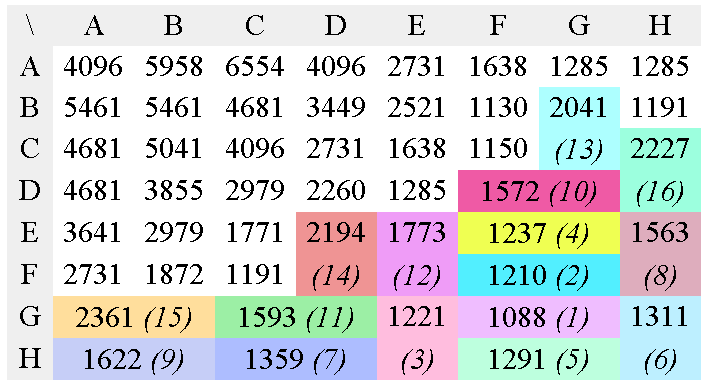
c) First Huffman pass
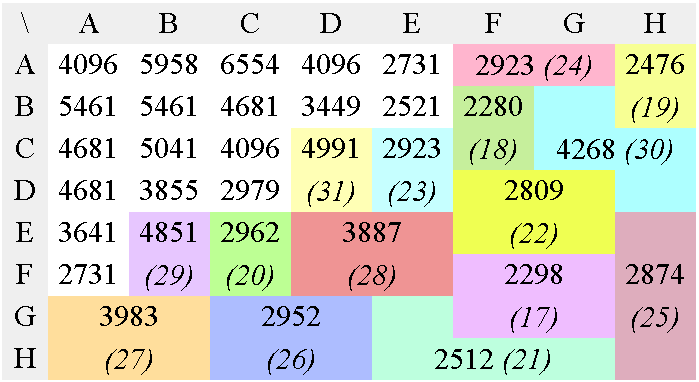
d) 2nd Huffman pass
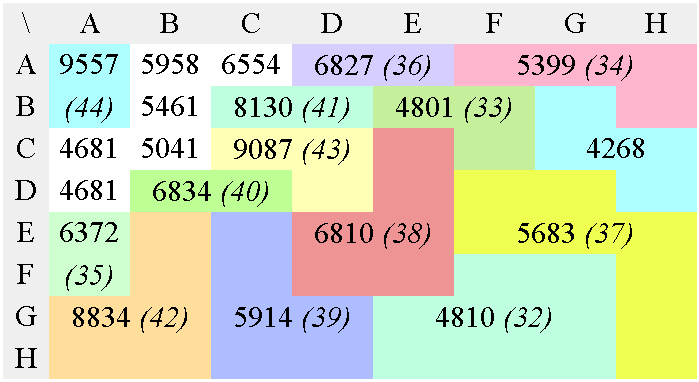
e) 3rd Huffman pass
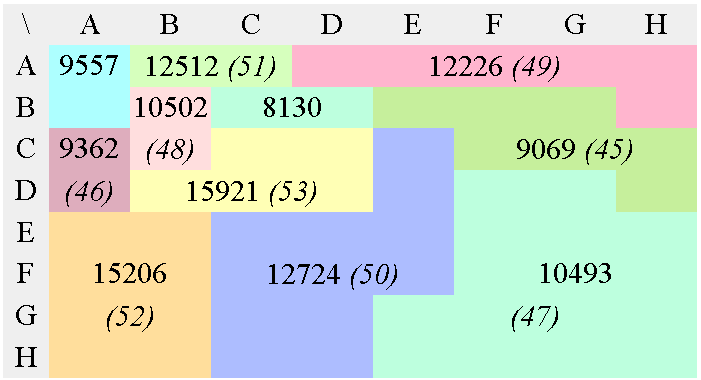
f) 4th Huffman pass

g) 5th Huffman pass
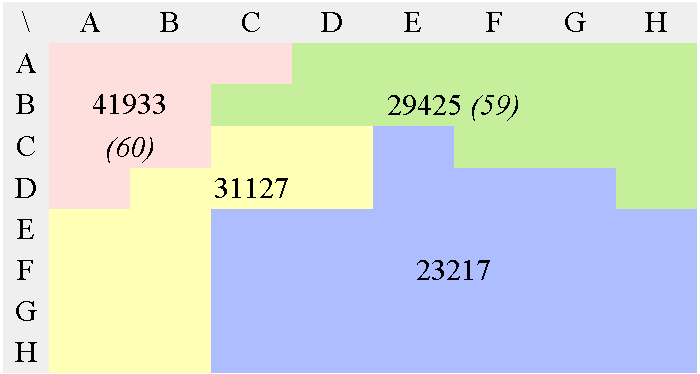
h) 6th Huffman pass
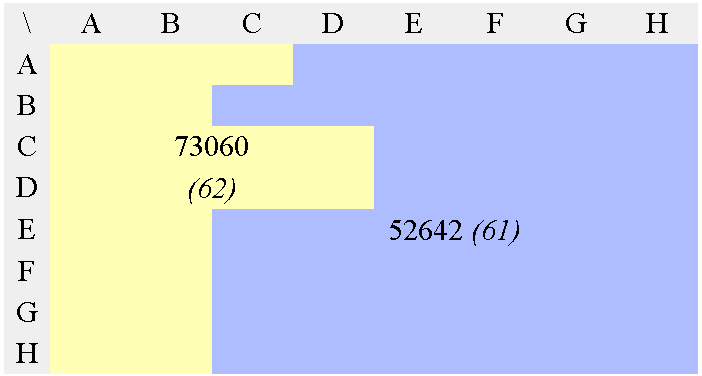
i) 7th Huffman pass
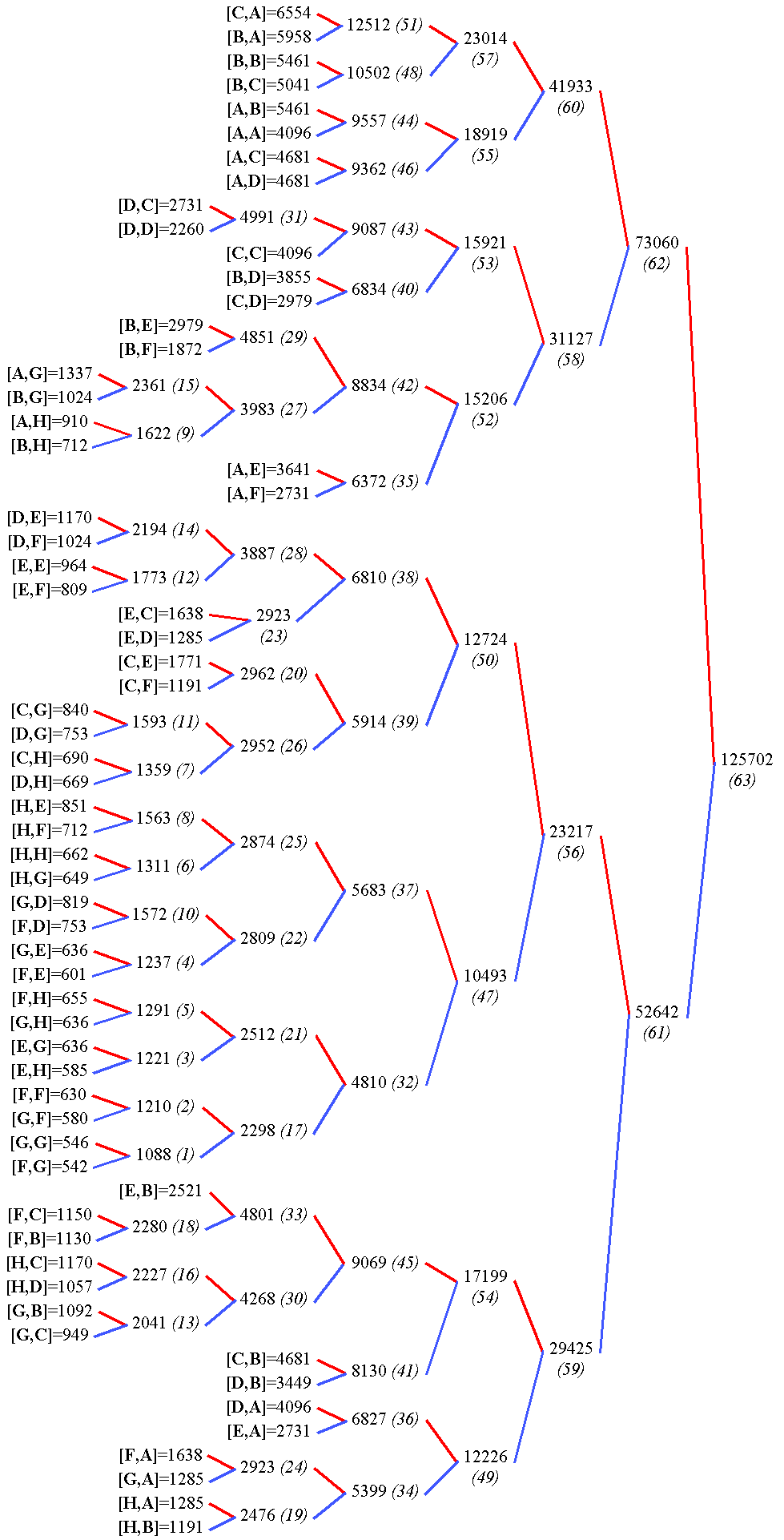
This 3R version performs the equivalent of the zig-zag, RLE and Huffman VLC steps of the "baseline JPEG" in a single operation, without the need to manage a Huffman table. This doesn't mean however that the coding efficiency is better, considering that JPEG and MPEG are the results of years of research and optimisation.
I have created the tree by hand for a special case where [A,A] (the DC result) is not encoded separately. Since the process is heavy and error-prone, I am not eager to recreate the tree for the "normal" JPEG case. In the future, I could write a program that generates the encoder and decoder's source code from a given matrix.
This article shortly presented most of 3R's main features and applications, in hope that others can use it and extend it. I am surprised that a minor algorithm originally intended for lossless sound compression can also be used in still or moving picture compression, or as backend to other transforms like FFT or BWT (this is yet do be examined). It's only the beginning, as many other ideas popped up spontaneously while writing this article.
Only basic operations on integer numbers are used, so 3R can be implemented easily in low-cost microcontrollers. It could also be coded in VHDL or Verilog for inclusion in a FPGA or ASIC.
3R is new to my knowledge. The closest algorithms that i am aware of are the Haar transform and the zerotree. The difference, however, is that 3R is mainly an encoder that directly generates a compacted bistream from suitable (transformed) data, while the others are transforms that require an additional entropy encoder (which could be 3R).
Most of the techniques presented here have not been extensively tested and compared with others. Keep in mind that my goal here is to explain rather than prove or demonstrate anything, particularly in such a space-constrained article about an unknown algorithm.
Many thanks to all the reviewers and particularly to Steven Pigeon for his insightful suggestions.
About the author: Yann Guidon, aka "whygee" (whygee@f-cpu.org), explores computers, electronics and music, designs microprocessors, builds printed circuit boards and develops various algorithms under GNU/Linux.