Actuellement, l'architecture du YASEP définit des instructions de multiplication partielles.
Initialement, l'idée était d'accéder à un multiplieur multi-cycles au travers des Registres Spéciaux mais cela aurait rendu les changements de contextes trop complexes.
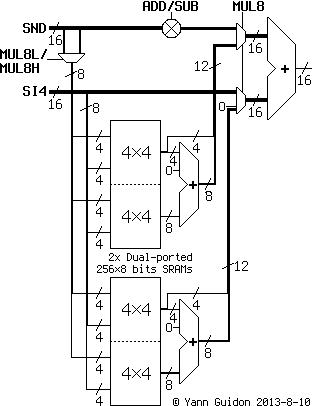
La méthode actuelle calcule un produit en assemblant les résultats de multiplications partielles. C'est un compromis entre la taille du code, la vitesse, la complexité matérielle et le multitasking. D'autres versions pourront utiliser des multiplieurs complets (au besoin, et si la technologie le permet) mais pour l'instant, le système réutilise l'additionneur 16 bits comme étage final, après deux additionneurs partiels de 12 bits, chacun additionnant les résultats sur 8 bits de quatre tables de multiplications 4×4 bits.

Cette méthode ajoute dynamiquement un étage au pipeline, chaque fois qu'une instruction MUL8L ou MUL8H est exécutée. En conséquence, une "bulle" d'un cycle est insérée dans le pipeline lorsque l'instruction suivante n'est pas une multiplication. Morale : il faut grouper les MULs.
Il y a 2 instructions de multiplication : MUL8L et MUL8H. Elles sont identiques mais MUL8H prend l'octet de poids fort de l'opérande SND, au lieu de l'octet de poids faible pour MUL8L. Cela simplifie un peu les séquences de code, en économisant quelques instructions de décalage ou rotation. (voir l'exemple R16×R16 plus bas).
Seules les multiplications non signées sont supportées pour l'instant. Les multiplicandes signés doivent être ajustés manuellement avant et après les séquences d'instructions.
; R1(8 bits) × R2(8 bits) => R2(16 bits) MUL8L R1 R2 ; 2 octets, instruction courte ; R1(8 bits) × R2(8 bits) => R3(16 bits) MUL8L R1 R2 R3 ; 4 octets, instruction longue
; R1(8 bits) × Imm16(8 bits) => R2(16 bits) MUL8L 123 R1 R2 ; 4 octets ; R1(8 bits) × Imm16(8 bits) => R1(16 bits) MUL8L 123 R1 ; est un alias vers : MUL8L 123 R1 R1 ; 4 octets aussi ; R1(8 bits) × Imm4(4 bits) => R1(12 bits) MUL8L 12 R1 ; 2 octets
YASEP16 : 6 instructions
; R1(8 bits) × R2(16 bits) => R3(16 LSB)-R4(8 MSB)
; R5 = temporaire
; moitié haute
MUL8H R1 R2 R3
SHR 8 R3 R4 ; répartit le résultat entre R3 et R4
SHL 8 R3
; moitié basse
MUL8L R1 R2 R5
ADD R5 R3
ADD 1 R4 R4 carry
; R1(8 bits) × Imm16 => R3(16 LSB)-R4(8 MSB)
; R2 = temporaire
; Imm16=1234h dans ces exemple
; moitié haute
MUL8L 12h R1 R3 ; 12h = 1234h>>8
SHR 8 R3 R4 ; répartit le résultat entre R3 et R4
SHL 8 R3
; moitié basse
MUL8L 34h R1 R2 ; 34h = 1234h & 0xFF
ADD R2 R3
ADD 1 R4 R4 carry
; (8 bits) × R2(16 bits) => R3(16 LSB)-R4(8 MSB)
; R5 = temporaire
; Imm8 = 12h dans cet exemple
; moitié haute
MUL8H 12h R2 R3
SHR 8 R3 R4 ; répartit le résultat entre R3 et R4
SHL 8 R3
; moitié basse
MUL8L 12h R2 R5
ADD R5 R3
ADD 1 R4 R4 carry
YASEP16 : 13 instructions
; R1 × R2 => R3-R4 (R5=scratch)
; R2 peut rester modifié (rotation) à la fin de cette séquence.
; les 2 octets du milieu sont calculés ensemble
MUL8H R1 R2 R3
MUL8H R2 R1 R4 ; observez l'échange des opérandes
ADD R4 R3 ; on réutilise la retenue plus tard
SHR 8 R3 R4 ; ajuste entre R3 et R4
SHL 8 R3
MOV 100h R5 ; (retenue spéculative)
OR R4 R5 R4 carry ; et met la retenue dans R4
; octet de poids faible
MUL8L R2 R1 R5
ADD R5 R3
ADD 1 R4 R4 carry
; octet de poids fort
ROL 8 R2
MUL8H R2 R1 R5
ADD R5 R4
; éventuellement :
ROR 8 R2
La table peut être réalisée avec des portes logiques ou une matrice de diodes spécialiée. Cependant certaines réalisations en FPGA peuvent utiliser des petits blocs de SRAM, en particulier sur cible Actel. Pour réaliser une multiplication de 8×8 bits, il faut disposer de 4 blocs de 4×4=8 bits de résultat. Deux blocs "dual port" de SRAM de 256 octets sont nécessaires. Les 4 tables peuvent être initialisées avec des valeurs identiques donc il n'y a que 256 valeurs à stocker et écrire. C'est réalisé par le code suivant :
; Code d'initialisation de la table de multiplication :
; R1 : SND (première adresse + compteur de boucle externe)
; R2 : SI4 (deuxième adresse (octet bas) + valeur initiale (octet haut))
; R3 : accumulator : incrément de la deuxième adresse + incrément initial (octet haut)
; R4 : compteur de boucle interne, encodée par position de bit (1-hot)
; A1 : adresse de la boucle externe
; A2 : adresse de la boucle interne
mov 0 R1
mov 11h R3
mov 1 R4
add 4 PC A1
; boucle externe, 16 itérations :
mov 0 R2
add 4 PC A2
; boucle interne, 16 itérations :
ADD R3 R2
MULI R2 R1
ror 1 R4
mov A2 PC LSB0 R4
add 100h R3
add 1011h R1
mov A1 PC no_carry
Actuellement, il n'y a pas d'instruction pour la multiplication signée, il faut donc ajouter du code qui ajuste le signe du résultat.
; Ajuste le résultat d'une multiplication R1xR2=>R3 ; D'abord, sauver calculer et sauver le signe dans R4 xor R1 R2 R4 ; ensuite ajuster le signe des opérandes sub 0 R1 MSB1 R1 sub 0 R2 MSB1 R2 ; équivalent d'ABS (valeur absolue) ; La multiplication MUL8L R1 R2 R3 ; l'ajustement : sub 0 R3 MSB1 R4
La version YASEP32 peut réaliser des multiplications 8×8 et 16×16 bits mais cela reste optionnel. La multiplication 16×16 bits est envisagée mais sa réalisation n'est pas encore prévue. Cela devrait être possible sur certains FPGA mais ce sera moins évident en ASIC.
MUL16H et MUL16L sont des version 16×16 bits de MUL8L et MUL8H. Ces instructions 16 bits peuvent donc être combinées de la même façon que les instructions 8 bits. Voici d'ailleurs l'adaptation des exemples précédents :
.profile YASEP32 ; R1(16 bits) × R2(16 bits) => R2(32 bits) MUL16L R1 R2 ; 2 octets, forme courte ; R1(16 bits) × R2(16 bits) => R3(32 bits) MUL16L R1 R2 R3 ; 4 octets, forme longue
.profile YASEP32 ; R1(16 bits) × Imm16(16 bits) => R2(32 bits) MUL16L 12345 R1 R2 ; 4 octets ; R1(16 bits) × Imm16(16 bits) => R1(16 bits) MUL16L 12345 R1 ; est un alias vers : MUL16L 12345 R1 R1 ; 4 octets aussi ; R1(16 bits) × Imm4(4 bits) => R1(12 bits) (attention : non signé !) MUL16L 12 R1 ; 2 octets ; Cet opcode court peut être "étendu" avec une condition : MUL16L 12 R1 R2 NZ R3 ; 4 bytes
; R1(16 bits) × R2(32 bits) => R3(32 bits poids faible)-R4(16 bits poids fort)
; R5 = scratch
.profile YASEP32
; moitié supérieure
MUL16H R1 R2 R3
SHR 16 R3 R4 ; répartit le résultat entre R3 et R4
SHL 16 R3
; moitié inférieure
MUL16L R1 R2 R5
ADD R5 R3
ADD 1 R4 carry
; R1(16 bits) × Imm16-Imm16 => R3(32 bits poids faible)-R4(16 bits poids fort)
; R2 = scratch
; Imm=12345678h dans cet exemple
.profile YASEP32
; moitié supérieure
MUL16L 1234h R1 R3 ; 1234h = 12345678h>>16
SHR 16 R3 R4 ; répartit le résultat entre R3 et R4
SHL 16 R3
; moitié inférieure
MUL16L 5678h R1 R2 ; 34h = 12345678h & 0xFFFF
ADD R2 R3
ADD 1 R4 carry
; Imm16 × R2(32 bits) => R3(32 bits poids faible)-R4(16 bits poids fort)
; R5 = scratch
; Imm16 = 1234h dans cet exemple
.profile YASEP32
; moitié supérieure
MUL16H 1234h R2 R3
SHR 16 R3 R4 ; répartit le résultat entre R3 et R4
SHL 16 R3
; moitié inférieure
MUL16L 1234h R2 R5
ADD R5 R3
ADD 1 R4 carry
; R1 x R2 => R3-R4 (R5=scratch)
; R2 may be left modified (rotated) after execution
.profile YASEP32
; Les 2 parties du milieu sont calculées ensemble
MUL16H R1 R2 R3
MUL16H R2 R1 R4
ADD R4 R3 ; la retenue est utilisée un peu plus tard
SHR 16 R3 R4 ; répartit le résultat entre R3 et R4
SHL 16 R3
MOV 10000h R5 ; retenue spéculative
OR R5 R4 carry ; ajoute la retenue dans R4
; demi-mot inférieur
MUL16L R2 R1 R5
ADD R5 R3
ADD 1 R4 R4 carry
; demi-mot supérieur
ROL 16 R2
MUL16H R2 R1 R5
ADD R5 R4
; eventuellement :
ROR 16 R2