The current architecture of the YASEP defines partial multiply instructions.
In the beginning of the architecture, there was the idea of an optional multi-cycle hardware multiplier that was meant to be accessed through the Special Registers. However this would have made interrupts and multi-processing difficult, as context switches would be too complex.
The currently chosen method computes only parts of a multiply. It is a compromise between code size, speed, context switching (multitasking) complexity and hardware complexity.
The planned implementation reuses the existing 16-bit adder (in the ASU unit) as a final stage, after 2 12-bit partial adders, each adding the 8-bit results of four 4×4 bits multiply tables.

This method adds 1 stage to the pipeline whenever MUL8L or MUL8H is executed. As a consequence, one "bubble" may be inserted in the pipeline the first time a non-multiply instruction is executed after a multiply instruction. Is it therefore advised to group MUL instructions together.
There are two 8-bits multiply instructions : MUL8L and MUL8H. They are identical but MUL8H takes the high byte of the SND operand, instead of the lower byte as in MUL8L. This simplifies the algorithms that multiply more than one byte, sparing a few instructions (see the R16×R16 example below).
Only unsigned multiplies are supported now. Signed multiplicands must be manually adjusted before and after the instruction sequence (see below).
; R1(8 bits) × R2(8 bits) => R2(16 bits) MUL8L R1 R2 ; 2 bytes, short encoding ; R1(8 bits) × R2(8 bits) => R3(16 bits) MUL8L R1 R2 R3 ; 4 bytes, long encoding
; R1(8 bits) × Imm16(8 bits) => R2(16 bits) MUL8L 123 R1 R2 ; 4 bytes ; R1(8 bits) × Imm16(8 bits) => R1(16 bits) MUL8L 123 R1 ; is an alias to : MUL8L 123 R1 R1 ; 4 bytes anyway ; R1(8 bits) × Imm4(4 bits) => R1(12 bits) MUL8L 12 R1 ; 2 bytes
YASEP16 : 6 instructions
; R1(8 bits) × R2(16 bits) => R3(16 lower bits)-R4(8 higher bits)
; R5 = scratch
; higher half
MUL8H R1 R2 R3
SHR 8 R3 R4 ; split the result between R3 and R4
SHL 8 R3
; lower half
MUL8L R1 R2 R5
ADD R5 R3
ADD 1 R4 carry
; R1(8 bits) × Imm16 => R3(16 lower bits)-R4(8 higher bits)
; R2 = scratch
; Imm16=1234h in this example
; higher half
MUL8L 12h R1 R3 ; 12h = 1234h>>8
SHR 8 R3 R4 ; split the result between R3 and R4
SHL 8 R3
; lower half
MUL8L 34h R1 R2 ; 34h = 1234h & 0xFF
ADD R2 R3
ADD 1 R4 carry
; (8 bits) × R2(16 bits) => R3(16 lower bits)-R4(8 higher bits)
; R5 = scratch
; Imm8 = 12h in this example
; higher half
MUL8H 12h R2 R3
SHR 8 R3 R4 ; split the result between R3 and R4
SHL 8 R3
; lower half
MUL8L 12h R2 R5
ADD R5 R3
ADD 1 R4 carry
YASEP16 : 13 instructions
; R1 x R2 => R3-R4 (R5=scratch)
; R2 may be left modified (rotated) after execution
; the 2 middle bytes are computed together
MUL8H R1 R2 R3
MUL8H R2 R1 R4 ; Notice the exchange of operands
ADD R4 R3 ; carry reused later
SHR 8 R3 R4 ; adjust between R4 and R3,
SHL 8 R3
MOV 100h R5 ; speculative carry
OR R5 R4 carry ; and put the eventual carry back into R4
; lower byte
MUL8L R2 R1 R5
ADD R5 R3
ADD 1 R4 carry
; higher byte
ROL 8 R2
MUL8H R2 R1 R5
ADD R5 R4
; eventually :
ROR 8 R2
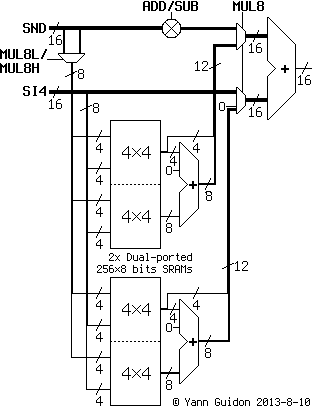
Some FPGA implementations might use small SRAM blocks as a multiply accelerator (on Actel chips, in particular). For 8×8 bits multiplies, there are 4 blocks of 4×4=8 bits of result. Two dual-port 256-byte SRAM blocks (at least) are necessary. The 4 LUTs can be initialised with the same values so there are 256 values to write. The following code provides a short routine that does this :
; LUT initialisation code :
; R1 : SND (first address + outer loop counter)
; R2 : SI4 (second address (lower byte) + init value (higher byte))
; R3 : accumulator : second address increment + init increment (higher byte)
; R4 : inner loop counter, 1-hot encoded
; A1 : outer loop address
; A2 : inner loop address
mov 0 R1
mov 11h R3
mov 1 R4
add 4 PC A1
; outer loop 16 times :
mov 0 R2
add 4 PC A2
; inner loop 16 times :
ADD R3 R2
MULI R2 R1
ror 1 R4
mov A2 PC LSB0 R4
add 100h R3
add 1011h R1
mov A1 PC no_carry
; the end
There is currently no signed multiply instruction and the result must be adjusted with additional code, such as:
; Adjust the result of a R1xR2=>R3 multiply ; First, compute and save the sign in R4 xor R1 R2 R4 ; the adjust the operands with their absolute value sub 0 R1 MSB1 R1 sub 0 R2 MSB1 R2 ; The actual multiply operantion MUL8L R1 R2 R3 ; Ajust the result : sub 0 R3 MSB1 R4
The YASEP32 flavor can support both 8×8 and 16×16 bits multiply opcodes (but they are optional). MUL16 is planned but not designed yet, I guess it might be easy to implement in some FPGAs but ASIC might be harder.
MUL16H and MUL16L are 16-bits versions of MUL8L and MUL8H and may be combined like the MUL8 opcodes above. Here are some example, adapted from the previous paragraphs:
.profile YASEP32 ; R1(16 bits) × R2(16 bits) => R2(32 bits) MUL16L R1 R2 ; 2 bytes, short encoding ; R1(16 bits) × R2(16 bits) => R3(32 bits) MUL16L R1 R2 R3 ; 4 bytes, long encoding
.profile YASEP32 ; R1(16 bits) × Imm16(16 bits) => R2(32 bits) MUL16L 12345 R1 R2 ; 4 bytes ; R1(16 bits) × Imm16(16 bits) => R1(16 bits) MUL16L 12345 R1 ; is an alias to : MUL16L 12345 R1 R1 ; 4 bytes anyway ; R1(16 bits) × Imm4(4 bits) => R1(12 bits) (remember : unsigned !) MUL16L 12 R1 ; 2 bytes ; This short opcode, like the others, can be "extended" and have a condition: MUL16L 12 R1 R2 NZ R3 ; 4 bytes
; R1(16 bits) × R2(32 bits) => R3(32 lower bits)-R4(16 higher bits)
; R5 = scratch
.profile YASEP32
; higher half
MUL16H R1 R2 R3
SHR 16 R3 R4 ; split the result between R3 and R4
SHL 16 R3
; lower half
MUL16L R1 R2 R5
ADD R5 R3
ADD 1 R4 carry
; R1(16 bits) × Imm16-Imm16 => R3(32 lower bits)-R4(16 higher bits)
; R2 = scratch
; Imm=12345678h in this example
.profile YASEP32
; higher half
MUL16L 1234h R1 R3 ; 1234h = 12345678h>>16
SHR 16 R3 R4 ; split the result between R3 and R4
SHL 16 R3
; lower half
MUL16L 5678h R1 R2 ; 34h = 12345678h & 0xFFFF
ADD R2 R3
ADD 1 R4 carry
; Imm16 × R2(32 bits) => R3(32 lower bits)-R4(16 higher bits)
; R5 = scratch
; Imm16 = 1234h in this example
.profile YASEP32
; higher half
MUL16H 1234h R2 R3
SHR 16 R3 R4 ; split the result between R3 and R4
SHL 16 R3
; lower half
MUL16L 1234h R2 R5
ADD R5 R3
ADD 1 R4 carry
; R1 x R2 => R3-R4 (R5=scratch)
; R2 may be left modified (rotated) after execution
.profile YASEP32
; the 2 middle halfwords are computed together
MUL16H R1 R2 R3
MUL16H R2 R1 R4 ; Notice the exchange of operands
ADD R4 R3 ; carry reused later
SHR 16 R3 R4 ; adjust between R4 and R3,
SHL 16 R3
MOV 10000h R5 ; speculative carry
OR R5 R4 carry ; and put the carry back into R4
; lower halfword
MUL16L R2 R1 R5
ADD R5 R3
ADD 1 R4 R4 carry
; higher halfword
ROL 16 R2
MUL16H R2 R1 R5
ADD R5 R4
; eventually :
ROR 16 R2